Are you taking the AP Calculus AB exam this spring and want to be well prepared on test day? The AP Calculus AB exam in 2022 will be held on Monday, May 9, at 8 am.
Before you sit down to take the exam, though, it's critical that you know how the Calculus AB test is formatted, what topics it covers, and how you'll be scored on it. This guide will go over all of that information while also showing you official sample problems and giving you tips on the best way to prepare for AP Calculus AB.
The AP Calculus AB exam can sometimes seem overwhelming, but we're here to break it down into clear and manageable information for you. You can also check out the College Board's new AP Classroom tool for AP Calculus AB, which has additional resources and information. Let's get started!
What's the Format of the AP Calculus AB Exam?
The AP Calculus AB exam is three hours and 15 minutes long and has two sections. Both of these sections are divided into two parts (based on whether or not a calculator is allowed).
Multiple-Choice Section
Here is an overview of the format of the AP Calculus AB multiple-choice section:
- 45 questions total
- One hour 45 minutes total
- Worth 50% of your total score
- Part A
- 30 questions
- 60 minutes
- No calculator allowed
- Part B
- 15 questions
- 45 minutes
- Calculator required
Note that the AP Calculus AB exam has had small changes made to its format. Previously, Part A of the multiple-choice section had 28 questions, and Part B had 17 questions.
Free-Response Section
Here is a rundown of the format of the AP Calculus AB free-response section:
- Six questions total
- One hour 30 minutes total
- Worth 50% of your total score
- Part A
- Two questions
- 30 minutes
- Calculator required
- Part B
- Four questions
- 60 minutes
- No calculator allowed
This can all look a little complicated, but basically, the AP Calculus AB exam consists of four parts. The first two are multiple choice, and the last two are free response.
You are required to use a calculator for the middle two parts (one each for multiple choice and free response), but you may not use a calculator for the first and last parts of the exam.
What Topics Does the AP Calculus AB Exam Cover?
Content on the Calculus AB exam can be divided into three main topic areas, referred to by the College Board as Big Ideas. Within these three Big Ideas are more specific topics called Enduring Understandings (often abbreviated as "EU"). Each Enduring Understanding contains both Learning Objectives and Essential Knowledge that the student should have learned by the time of the exam.
As I mentioned, there have been some updates to the AP Calculus AB exam. Namely, the Big Ideas are now integrated within each of the eight units covered in the AP Calculus AB course.
The good news is that there haven't been any changes to the structure of the AP Calculus AB exam!
I've listed each of the Big Ideas and their Learning Objectives below, since these are the most relevant for students looking for what the exam covers.
For the sake of length and clarity, I left out the Enduring Understandings and Essential Knowledge. If you'd like to see these, as well as more detailed information on the content covered by the exam, check out the official AP Calculus AB Course Description. Still, know that the information below will give you a solid look at what you're expected to know for the exam.
Learning Objectives are listed below Big Ideas. These Learning Objectives are skills that students are expected to know how to do for the exam.
Big Idea 1: Change
- Understand how and when change occurs
- Determine the rate of change
- Interpret how different equations are structurally similar
- Determine change over an interval of time
- Analyze functions for intervals of continuity or points of discontinuity
- Determine the applicability of important calculus theorems using continuity
- Find the rate of change based on the area of a region between a curve and the x-axis
- Model motion not constrained to a linear path
Big Idea 2: Limits
- Understand limits, and making sense of features of functions and their graphs
- Mathematical properties and rules for simplifying and evaluating limits applies to differentiation
- Prove a limit exists
- Recognize the connection between differentiability and continuity
- Interpret the meaning of a derivative within a problem
- Solve problems involving the slope of a tangent line
- Solve problems involving related rates, optimization, and rectilinear motion
- Solve problems involving rates of change in applied contexts
- Solve how the sum if infinitely discrete terms can be a finite value represented in a continuous function.
Big Idea 3: Analysis of Function
- Close loopholes so a conclusion about a function is always true
- Understand how the change of two units of measurement relate to one another, and the rate at which they change.
- Interpret what numbers might tell you about other rates of change
- Apply the Mean Value Theorem to to justify a conclusion
- Include additional information in a sound mathematical argument that optimizes a simple equation
- Integrate to find areas related to differentiating to find slopes
- Calculate derivatives and antiderivatives
- Evaluate definite integrals
- Analyze graphs defined using parametric equations or polar functions using chain rules.
- Apply definite integrals to problems involving the average value of a function, motion, and area and volume.
- Analyze differential equations to obtain general and specific solutions
- Interpret, create, and solve differential equations from problems in context
AP Calculus AB Units
Since the Big Ideas of AP Calc AB are covered throughout the course, it's also useful to know what each unit covers.
In the table below, you'll find each of the course's units, along with a brief description of the topics covered in that unit. We've also included the weighted breakdown of questions on the AP Calc AB exam that come from each unit. So for example, 10-12% of your exam grade will come from questions about Limits and Continuity, while 17-20% of your exam grade will come from questions about Integration and Accumulation of Change.
| AP Calculus Unit | Major Topics | Exam Weighting (%) |
| Unit 1: Limits and Continuity |
|
10-12% |
| Unit 2: Differentiation: Definition and Fundamental Properties |
|
10-12% |
| Unit 3: Differentiation: Composite, Implicit, and Inverse Functions |
|
9-13% |
| Unit 4: Contextual Applications of Differentiation |
|
10-15% |
| Unit 5: Analytical Applications of Differentiation |
|
15-18% |
| Unit 6: Integration and Accumulation of Change |
|
17-20% |
| Unit 7: Differential Equations |
|
6-12% |
| Unit 8: Applications of Integration |
|
10-15% |
Knowing the topics covered in AP Calc AB, along with how they factor into your AP exam score, will help guide your studying and make it more productive!
Also, keep in mind there's a lot more to know about these units and unit topics. For more information, be sure to check out the official AP Calculus AB Course Guide provided by the College Board.
AP Calculus AB Sample Questions
Looking at sample questions is one of the best ways to get a feel for what the AP Calculus AB exam will be like. Here are four sample questions, one from each part of the AP exam. Each of these questions was taken from the official AP Calculus AB Course Description, which you can look at for more complete answer explanations and additional sample problems.
Multiple Choice (No Calculator)
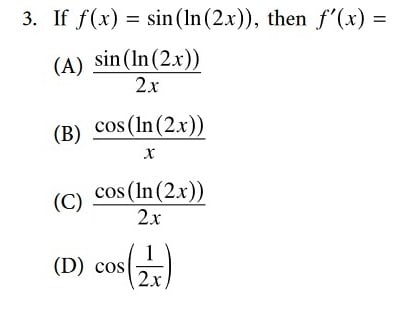
This question tests your ability to calculate derivatives. You'll need to use the chain rule to differentiate composite functions. The correct answer to this problem is B.
Multiple Choice (Calculator Allowed)
This question tests your ability to solve problems with rapid rates of change. You'll have to find the derivative in order to find the rate of change of the temperature of the water. The correct answer is B.
Free Response (Calculator Allowed)
This question tests your knowledge of integrals. Parts A, B, and C are each worth 3 points.
Free Response (No Calculator)
This question tests your knowledge of multiple topics, including derivatives and integrals. You can receive up to 1 point for part A, 2 points for part B, and 3 points each for parts C and D.
How Is the AP Calculus AB Exam Scored?
As mentioned, the multiple-choice section and the free-response section are each worth 50% of your total exam score.
For the multiple-choice section, you earn 1 point for each question you answer correctly. No points are deducted for incorrect answers, so you should answer every question! You can earn up to 45 points for this section.
For the free-response section, each of the six questions is worth 9 points, so you can earn up to 54 points. Different parts of each question can be worth a different amount of points (for example, on one question you may be able to earn up to 1 point for part A, 3 points for part B, 3 points for part C, and 2 points for part D).
After your points are added up for each of your sections, your AP Calculus AB score is converted to the standard AP scoring scale of 1-5. The exact formula for doing this can change slightly from year to year.
However, in 2008, the process for converting raw AP scores to scaled scores involved multiplying the number of multiple-choice questions you answered correctly by 1.2272, and then adding that number to the points you received on the free-response section. This value is rounded to the nearest whole number and becomes your composite score.
Each AP score (from 1-5) corresponds to a range of composite scores. Below, you can see the conversion chart and score distributions for test takers from the 2020 Calculus AB exam:
| Composite Score Range | AP Score | % of Students Who Got Score |
| 0-26 | 1 | 19% |
| 27-38 | 2 | 20.4% |
| 39-51 | 3 | 20.5% |
| 52-67 | 4 | 24.1% |
| 68-108 | 5 | 16% |
Source: The College Board
3 Tips for Preparing for the AP Calculus AB Exam
Studying for the AP Calculus AB exam can be tough. Use these three tips to make your studying more effective and increase your chances of getting a great score.
Tip 1: Memorize Important Formulas
There are certain formulas for AP Calculus AB that you should have down pat. There's no formula sheet given on the AP exam, so you'll have to memorize the formulas you'll need. Many teachers give out formula sheets for students to memorize.
There are also various formula cheat sheets you can use to review before the exam. To find these, simply Google "AP Calculus AB formula sheet" and look at your options.
In general, any formula you use regularly in class is a good one to memorize. Major formulas you should have memorized include those for limits, differentiation, and integration, as well as the fundamental theorems.
Tip 2: Know How to Use Your Calculator
You're allowed to use your calculator for two of the four exam parts, and most of the questions in these two sections will be difficult, if not impossible, to solve without a graphing calculator.
While it might seem obvious that you should know how to work your calculator, knowing exactly how and when to use its different functions can save you a lot of time on the exam and increase your chances of getting the correct answer.
According to the College Board, the four calculator capabilities you'll use the most during the AP Calculus AB exam and should easily be able to do with your calculator are as follows:
- Plot the graph of a function within an arbitrary viewing window
- Find the zeros of functions (solve equations numerically)
- Numerically calculate the derivative of a function
- Numerically calculate the value of a definite integral
When you're preparing for the exam, be sure that you know how to do each of these (completing practice problems can help!).
Tip 3: Get Used to Showing All Your Work
For most free-response questions on the AP Calculus AB test, the final answer to a problem is only worth 1-2 points out of a possible 9. This means that the majority of points are earned through intermediate steps of the problem—and if you don't show how you reached those intermediate steps, you won't get a high score on this section.
Even if you get a correct answer by using your calculator, you have to write the setup (such as the equation being solved or the derivative being evaluated) as well as the answer in order to get credit for your work.
You might be used to not writing down certain work that seems particularly obvious on homework and class tests. However, even if your teacher doesn't mind, AP graders will.
Remember that AP graders are more interested in how you reached your final answer than they are in what that final answer is, so get yourself in the habit of showing each step of your work well before exam time.
Conclusion: What to Know About the AP Calculus AB Exam
The AP Calculus AB exam can be intimidating if you don't know what to expect. Knowing how the exam will be formatted and what types of questions it will ask can go a long way toward helping you feel more prepared and confident on test day.
The exam has two sections, multiple-choice and free-response, which are each divided into two parts, based on whether or not you may use a calculator. Each of these sections is worth 50% of your total AP score.
The exam itself covers three main topics:
- Limits
- Derivatives
- Integrals and the Fundamental Theorem of Calculus
In order to prepare for the AP Calculus AB exam in the best way, keep these three tips in mind during your review:
- Memorize important formulas
- Know how to use your calculator
- Get used to showing all your work
What's Next?
Now that you know what the AP Calculus AB exam covers, the next step is to practice! Read our guide to get links to every Calculus AB practice test available online.
Wondering how challenging other AP classes are? Learn what the easiest AP classes are and what the hardest AP classes are so that you know exactly what to expect!
Not sure which other math classes you should take? Math is often the trickiest school subject to choose classes for, but our guide will help you figure out exactly which math classes to take for each year of high school.
