On average, you’ll need to use an SAT math formula once every four to five questions. This accounts for approximately 20-25% of the combined math sections, which means it is crucial that you understand how and when to employ your formulas on the SAT.
We’ve put together the list of your need-to-know SAT formulas (prioritized in the order from greatest to least that you’ll see them on the SAT) as well as how to best use them for test-day.
What Formulas Will You Need on the SAT?
You will always be given nine geometry formulas and two geometry laws on the test, but NO algebra or coordinate geometry formulas.
We’ve put together a list of the 21 SAT math formulas you should know for test day and prioritized them according to “need to know” and “good to know.” If you feel rusty on any formula or math topic on the list, check out one of our individual math topic guides to see how the formula works (and even why it works), as well as how to recognize when to use it. We’ll also show you the alternatives to using formulas for many questions.
For instance, you can solve your distance questions by either using the distance formula or by drawing a picture and using the Pythagorean Theorem. Both of these methods require formulas, but you are given the Pythagorean Theorem in the formula box, and so we have classified the distance formula as “good to know” but ultimately not “necessary.”
SAT math questions are designed to be solved in a multitude of ways, so don't worry about having to find the one "right" path.
How to Use Your Formulas Effectively
So how do you best utilize your formulas, both given and not given? Let’s take a look.
#1: MEMORIZE your formulas
The best thing you can do for yourself (and your SAT math score) is to memorize your formulas--yes, even the ones you’re given. Though it is nice to have the formula box as a fallback option to double-check your work, it is both a distraction and a time suck to continuously flip back and forth from problem to formula box, problem to formula box.
Dividing your focus like this can lead to careless errors and is not something that we recommend. Unless you, for any reason, cannot memorize your formulas, then absolutely do so. Memorization (and practice, to drill them into your head) is going to be one of the strongest tools in your belt when taking the SAT math section.
If you're a visual learner, make yourself a set of formula flash cards. If you're a kinesthetic (movement) learner, practice drawing and/or writing them out on a separate piece of paper. And if you're an auditory learner, get a parent or a friend to help you drill them aloud. Once you feel you've got your formulas down, practice using them on actual SAT questions to help you both remember them and learn how to use a particular formula for a particular problem. (We'll give you the opportunity to practice using your formulas in the next section.)
#2: Prioritize learning your most crucial formulas
Some formulas come up over and over (and over!), while others show up sparingly at best. If you are pressed for time, nervous about memorizing so many formulas, or simply trying to map out your plan of attack, memorize your formulas in the order that they appear most often on the test.
Of your “necessary” formulas, they appear on the test from greatest prevalence to least in roughly this order:
-
Law: the sum of the interior degrees of a triangle is 180
-
Area of a triangle
-
Law: the sum of the degrees of a straight line is 180
-
Area of a rectangle (or other quadrilateral)
-
Pythagorean Theorem
-
Finding slope of a given line (rise/run)
-
Finding slope of line connecting two points
-
Finding percentages
-
Law: the number of degrees of arc in a circle is 360
-
Area of a circle
-
Circumference of a circle
-
Finding averages
-
Area of a circle’s arc
-
Circumference of a circle’s arc
-
Finding probabilities
-
Finding combinations
-
Finding the midpoint of a line
-
Volume of rectangular solid
-
Volume of cylinder
Of the “good to know” or “shortcut” formulas, you will need them roughly in this order:
-
Special right triangle properties, 30-60-90
-
Special right triangle properties, 45-45-90
-
Arithmetic sequences
-
Geometric sequences
-
Distance formula
#3: Decide NOW which (if any) of your “good to know” formulas you want to memorize
The reason they are called “good to know” formulas is exactly how it sounds--you can find all the answers to your SAT math problems without knowing these formulas or shortcuts at all. On the other hand, knowing them can save you time and effort, so it’s entirely your decision whether or not to memorize them.
Just keep in mind that it is worse to remember a formula incorrectly than it is to have not attempted memorizing it at all. So if you do decide to memorize, say, the distance formula, make sure you’ve got it locked down tight. Otherwise, just decide here and now to only pay attention to your necessary formulas and leave the “good to know” formulas in the dust.
#4: Practice SAT math questions at home without looking up your formulas
It’s one thing to memorize your formulas with flash cards, but it’s a whole other ball game to remember them when you come face to face with real SAT math problems. You’ll have to figure out which formulas to use and how to execute them, in addition to remembering just what they are. And the only way you’re going to be able to do this is by practicing.
After you’ve made the effort to memorize your formulas, practice your SAT questions without the safety net. Try to solve them as if you were really taking the test--so memorize your formulas if possible, but feel free to use the given formulas as a fallback in case you get stuck or need to double-check your answers.
#5: Don’t panic if you forget a formula
Most of all don’t panic! We’ve said it before, and we’ll say it again--there are always multiple ways for you to solve your SAT math questions. So if you forget a formula, don’t worry about it!
Is it a problem that can’t be solved without a formula? You will always have your given formulas in your formula box to rely on in a pinch. Is it a problem that requires an algebraic (aka, NOT given) formula? Then you will likely be able to solve it in a way that does not require a formula. On most occasions, you will be able to use the strategies of plugging in answers, plugging in numbers, or even just making a logical guess, to help you solve questions that you otherwise cannot.
If necessary, you can usually eliminate one or two answer choices that are obvious outliers, even if you don’t know the formulas or strategies for how to solve the problem.
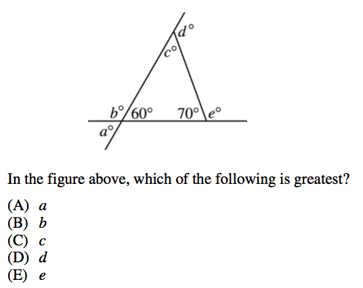
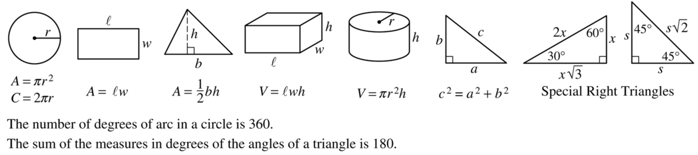
If, for any reason, you forgot your formulas and even forgot that you had a formula box at your disposal, you can still eliminate several answer choices for this problem. If we remember that all SAT figures are drawn to scale unless otherwise noted, we can see at a glance that angles $a$ and $c$ are clearly smaller than angles $b$, $d$, and $e$.
Eliminating two answer choices is enough to take a guess on the SAT and not risk too much with a wrong answer penalty, but we might be able to narrow it down even further. Even without knowing that a straight line has a degree measure of 180, we can logically deduce that a straight line must measure some amount and that all straight lines will be the same. The unknown angle attached to a given angle in a straight line (the supplementary angle) will therefore measure the remaining amount of the full measure of the line (whatever that measure may be).
To visualize this, let's say that you have two buckets full of tennis balls. Each bucket contains the exact same amount of tennis balls, even though you don't know how many that is. You remove two tennis balls from the first bucket and one tennis ball from the second. Even though you didn't know how many tennis balls there were to begin with in each bucket, we know that the second bucket must have more tennis balls remaining than the first.
This means that the angle attached (supplementary) to the larger given angle on a line will be smaller than the angle supplementary to the smaller given angle on a line. In other words, angle $e$ will be smaller than angle $b$, because $e$ is attached to a larger angle on a line. This means we can eliminate angle $e$ from the group.
This leaves us with two answer choices, $b$ and $d$, all without the use of any formulas whatsoever. By guessing now, we have a 50-50 shot of getting it right!
[Note: the correct answer is D, angle $d$.]
And, as a last resort, you can always skip the problem entirely. Remember: if you cannot eliminate any answer choices, then you’re better off skipping the problem and simply moving on. Pick up points where you can and cut your losses--a question here and there that you have to skip won’t affect your score as much as you may think.
Ready to test out your formula skills?
SAT Math Practice Using Formulas
Now let’s test your formula knowledge against real SAT math problems, all of which require formulas (both given and not given) to solve.
1)
2)
3)
4)
Answers: D, D, C, 8
Answer Explanations:
1) If we remember our solid geometry formulas, we know that the volume of a rectangular prism is found by:
$a = lwh$
So we can find the volume of our smaller rectangular blocks by multiplying the height, length, and width.
$3 * 2 * 1$
$6$ inches.
We can also find the volume of our larger prism the same way. We are told that the box is a cube, which means that the height, length, and width are all equal. If one side of the cube measures 6 inches, the volume of the cube will be:
$6 * 6 * 6$
$216$ inches.
Now we can simply divide the larger box by the smaller blocks.
$216/6$
$36$
36 smaller rectangular blocks will be able to fit into the larger box.
Our final answer is D, 36.
2) This is another problem we can pretty much eyeball and work through logically, without knowing much about circles. We can also work through it using our formulas properly, so let's look at both techniques.
Let's start by estimating.
We are told that the larger circle has a circumference of 36 and that the radius of the smaller circle is half the radius of the larger circle. We also know that the figure is to scale, since we are not told otherwise.
Even without knowing anything about circles, we can see that the cut out of 80° looks to be a little less than a quarter of both the larger and the smaller circle.
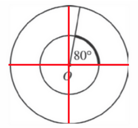
As you can see, the red lines would divide the circle into proper quarters, and 80° is a little less than this. So if we know that the larger circumference is 36, we can divide this by 4 to find the approximate length of the larger arc.
$36/4 = 9$
We know that the arc of the larger circle must be smaller than 9 (remember--80° is a little less than a quarter), so the arc of the smaller circle must be even smaller than this.
We can safely eliminate answer options A and B.
Now we can eyeball the difference between the arc measures and guess that, if the larger arc is close to 9, the smaller arc is probably larger than 2. This leaves us with two answer choices, C and D, which gives us a 50-50 chance of getting the right answer. It is a safe time to make our best guess.
Alternatively, we can solve the question by using our knowledge of circle formulas and angles.
We are told that the larger circle has a circumference of 36 and we know that, to find the circumference of a circle, we use the formula:
$c = π2r$
If the circumference is 36, then the radius must be $36/2 = 18$
This means that the radius of the smaller circle (which we were told is half the radius of the larger) must be 9.
Now, to find the circumference of an arc, we use the formula:
$c_{arc} = π2r(\angle/360)$
$18(80/360)$
$4$
Our final answer is D, 4.
3) We know that the area of a triangle is:
$a = {1/2}bh$
Imagine, then, that we are working with a right triangle. This way, we can use one of our leg measures as our height to get our maximum area.
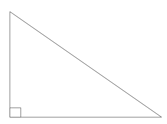
We also know that the hypotenuse of a right triangle will be the side opposite the 90 degree angle. So if 10 is the longest side (the hypotenuse), the base or the height would have to be smaller.
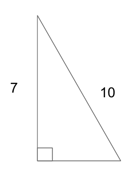
If, however, 10 acted as either the base or the height, the 7 would act as the other piece. This would mean our area was:
$a = {1/2}(10)(7)$
$a = 35$
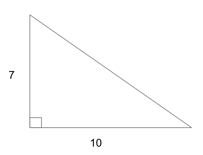
The largest possible area for our triangle is 35.
Our final answer is C, 35.
4) For this problem, let us first fill in our given information.
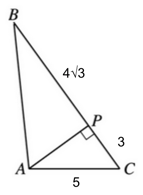
Now, we know that triangle APC is a right triangle, which means we can use either the Pythagorean Theorem (or our triangle shortcuts) to find the length of AP.
$a^2 + b^2 = c^2$
$a^2 + 3^2 = 5^2$
$a^2 + 9 = 25$
$a^2 = 16$
$a = 4$
AP = 4
Now triangle ABP is also a right triangle, because it is connected on a line to the right triangle APC. In other words, angles BPA and APC are supplementary.
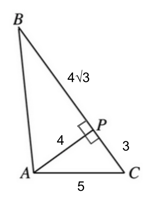
This means we can find the measure of leg BA by using the Pythagorean Theorem one more time.
$a^2 + b^2 = c^2$
$(4√3)^2 + 4^2 = c^2$
$16(3) + 16 = c^2$
$48 + 16 = c^2$
$64 = c^2$
$c = 8$
BA = 8.
Our final answer is 8.
You did it! It's done, yay!
Image: Travis Nep Smith/Flickr
The Take-Aways
Don’t underestimate the value of needing to both know and understand your SAT formulas, but don’t get too fixated on them either. Though problems that require formulas account for 20-25% of your overall SAT math questions, that still leaves 75-80% of all SAT math questions that DON’T require formulas at all.
So make sure that you know your formulas, but don’t think that knowing your formulas is the only hurdle to pass to do well on your SAT math test. Formula knowledge is just one step (though an important step) for doing well on the SAT math section as a whole. But a knowledge of your formulas, a balanced study plan, and a brush-up on any SAT math topic in which you might be rusty will definitely help get you to get where you need to be by test-day.
What’s Next?
Need to brush up on a particular SAT math topic? Check out our individual math topic guides for all your SAT math needs.
Running out of time on the SAT math section? We'll show you how to beat the clock and maximize your score before time runs out.
Been procrastinating in your SAT math study? Our guide will help you balance out your study time and beat back the urge to procrastinate.
Aiming for a perfect score? Check out our guide to getting an 800 on the SAT math section, written by a perfect-scorer.
