Polynomial problems will show up in some way, shape, or form on the ACT two or three times per test. And since polynomials are so deeply connected to other ACT math topics, like operations and functions, it's even more important to take the time to understand them before test day.
Luckily, you probably know a lot more about polynomials than you think, and if you're currently rusty on the subject, just a little review will have you knocking out your polynomial questions left and right.
This will be your complete guide to polynomials on the ACT—what they are, how you'll see them on the test, and the best way to solve your polynomial problems before time is up.
Feature image credit: Linas/Wikimedia
What Are Polynomials?
A polynomial is any mathematical expression that contains variables, constants, coefficients, and/or non-negative integer exponents. This means that polynomials cover a wide variety of mathematical expressions, so let's break this down.
Variable: A variable is any symbol that acts as a placeholder for an unknown value. Some of the most common variables on the ACT are $x$ and $y$.
Constant: A constant is any number that exists as a fixed value. For instance, both 7 and -3.278 are constants.
Coefficient: A coefficient is any value that is multiplied by a variable. In the term $5x$, 5 acts as a coefficient because it indicates that the variable $x$ is being multiplied five times.
Non-negative integer exponent: If we break this term down, a non-negative integer exponent is exactly how it sounds; it is any positive exponent that is also an integer. For instance, $x^3$ fits the definition, but $x^{-2}$ or $x^{1/2}$ does NOT.
A polynomial can consist of a single term or multiple terms in a relationship with one another. The values in a polynomial can be added, subtracted, multiplied, or divided together so long as no part of the polynomial value is divided by a variable. For instance, a term of the polynomial could be $4/15$ or $x/4$, but NOT $4/x$.
Polynomials can have no variable (e.g. 4), one variable (e.g. $2x^2 - 6x + x$), or multiple variables (e.g. $y(2xy - 8x + 5z) - q^3$).
Examples of Polynomials
6
$12x$
$14 + 2x$
$3y^2 - 4x + 2$
$(75k * 23x^12) + 8$
${3z - 59 + 6x^7}/5$
NOT Polynomials
$2x^{-4}$
(Why not? A polynomial cannot have a negative exponent.)
$xy^{2/3}$
(Why not? A polynomial cannot have a fractional exponent.)
$6/{2 - x}$
(Why not? A polynomial cannot have any term that is divided by a variable.)
Degree of Polynomial
Polynomials have degrees and you can tell the degree measure of the polynomial by looking at its exponents. The degree of the polynomial is the value of the largest exponent. For instance, the polynomial $x^2 - 6x + x^3$ has a degree of 3, since the largest exponent value is 3.
If the polynomial has no variable (e.g., if the polynomial is simply "9"), the degree measure is 0. And if there is no exponent (e.g., $4x + 2$), then the degree measure is 1.
[Note: this only applies is the polynomial has a single variable or no variable. You cannot do this for the polynomial $x^3 - 6y^2 + y^5$, for instance, because it has two variables, $x$ and $y$.]
Why is it good to know the degree of a polynomial?
The degree measure of a polynomial tells us what the graph of a polynomial looks like.
|
Degree Measure |
Graph Type |
|
0 |
Constant |
|
1 |
Linear |
|
2 |
Quadratic |
[Note: though there are more polynomial degree measures and types of polynomial graphs, these are the only ones you will see on the ACT.]
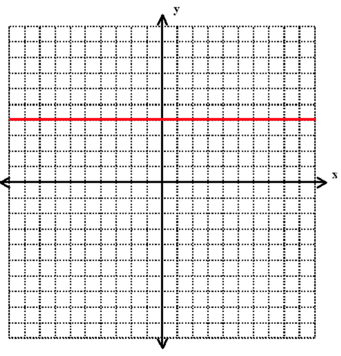
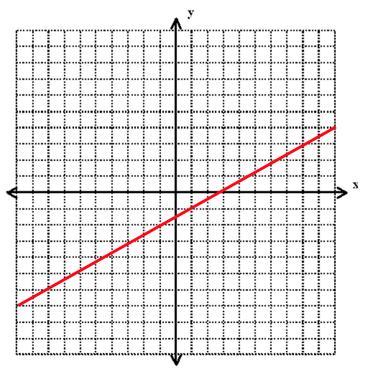
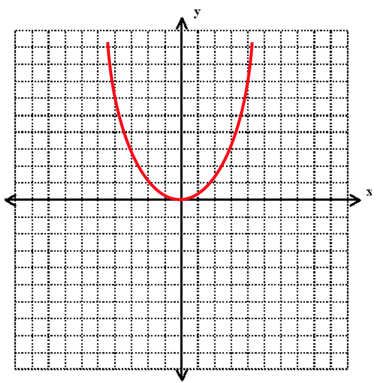
Once graphed, these polynomials will look like this:
Constant Graph
Linear Graph
Quadratic Graph
Now that we've looked at our pieces, let's see how they fit together.
How to Solve Polynomial Questions
To solve many constant and linear polynomial problems, you will need to have a basic understanding of operations problems and integers. You will also need to know your way around lines and slopes in the coordinate plane.
In this guide, however, we will be primarily focused on quadratics. For quadratic polynomials, you will have to understand how to use two mathematical techniques—factoring and FOIL-ing—to solve for your final solution. This concept is closely related to algebraic functions, so it's a good idea to tackle these topics simultaneously.
So let's look at factoring and FOIL-ing.
Factoring and FOIL-ing Polynomials
Factoring and FOIL-ing are ways of manipulating mathematical expressions and polynomials to expand or reduce the expressions and find the information you need. Again, on the ACT, you will be using both techniques together to find the solution(s) to 2nd degree polynomials (quadratics).
FOIL-ing
You will use this technique whenever you need to multiply two polynomials together. When you're given a series of parenthetical expressions and must multiply them, you must do so by FOIL-ing them out. "FOIL" stands for "first, outside, inside, last" and this mnemonic refers to the order in which you must multiply together the numbers in the parentheses before you add the results together.
To clarify this process, let's look at an example.
Say we needed to multiply these expressions:
$(2x - 3)(x + 5)$
According to FOIL, we must start by multiplying the "first" numbers of each expression. This will give us the F in our FOIL. In this case, that will be $2x$ and $x$.
$2x * x$
$2x^2$
Next, we must multiply the "outside" numbers in each expression. In this case, the outside numbers are $2x$ and $+5$
$2x * 5$
$10x$
Next up, we need to multiply our "inside" numbers, which will give us our I in our FOIL. In this case, our inside numbers will be $-3$ and $x$.
$-3 * x$
$-3x$
Finally, we must multiply our "last" numbers, which will give us the L in our FOIL. In this case, our last numbers will be $-3$ and $+5$.
$-3 * 5$
$-15$
Now, the final step is to add all of our components together.
$2x^2 + 10x - 3x - 15$
$2x^2 + 7x - 15$
This will be our final polynomial expression.
Factoring
Factoring goes hand in hand with FOIL-ing and acts basically as its reverse. In order to convert a longer polynomial (most often a quadratic equation) into smaller parenthetical expressions, we must factor the equation. This will eventually give us the two solutions to our quadratic function.
If you remember your functions, then you'll remember that a quadratic equation ($y = ax^2 + bx + c$) will have two solutions. These solutions are the two values of $x$ when $y$ (the $y$-intercept) equals zero.
For example, in the graph below:
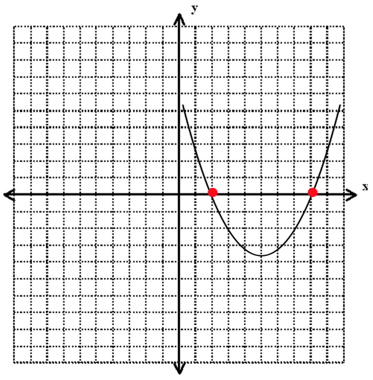
The solutions are at $x = 2$ and $x = 8$ because this is where the parabola crosses the $y$-intercept and so are the values of $x$ when $y = 0$.
Now, if we are instead given a parabola as a polynomial instead of as a graph, we can still find the solutions to the expression by factoring.
For instance, let us say that this is our quadratic equation:
$x^2 + x - 12$
We know we can factor this equation and we do so by setting up a potential FOIL that will lead us to the final result of this equation. So our parentheticals will look like this:
$(x +/-$ __$)(x +/-$ __$)$
We're not yet sure whether we will be adding or subtracting our integers in each equation and we don't yet know what the integers will be, but we do know that we will need a single $x$ value in each to give us our F of $x^2$ when we FOIL them out.
Now, we know that the L, last, numbers in the parenthesis will make the final integer value in our quadratic equation. This means that we know that the last two numbers in each of the parenthetical expressions must multiply together to equal -12.
Since we also know that the only way to multiply two numbers and get a negative, one number must be negative and one must be positive. This must mean that one of the parenthetical expressions will have a minus sign and the other must have a plus sign.
To equal -12, our potential integer value pairs could therefore be:
$-1, 12$
$-2, 6$
$-3, 4$
$-4, 3$
$-6, 2$
$-12, 1$
Now only one of these pairs of numbers will work as the solution to our equation, so let us test them out to see which will give us our original polynomial once we FOIL them.
$(x - 1)(x + 12)$
If we properly FOIL this expression, we will end up with:
$x^2 +12x - x -12$
$x^2 +11x - 12$
This does NOT give us the right equation, so we must try again with another pair of integers.
$(x - 2)(x + 6)$
$x^2 + 6x - 2x - 12$
$x^2 + 2x -12$
Again, this is NOT our original equation, so we know that this pair of integers is not correct. We must try again.
$(x - 3)(x + 4)$
$x^2 + 4x - 3x - 12$
$x^2 + x -12$
This DOES match our original equation and, since there can be only two solutions to any quadratic equation, we know that all the other pairs of numbers must be incorrect.
With this, we have now properly factored our polynomial/quadratic equation, but we still have one more step to go; we must complete the problem by setting each parenthetical expression to zero and solving for the $x$-value. Why? Because, again, the two solutions to any quadratic equation are the two values of $x$ when $y = 0$.
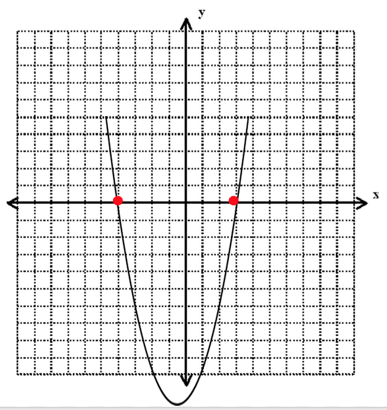
Spoiler alert: our parabola will look like this when graphed.
So let's take both our parentheticals and set them each to 0.
$(x - 3)(x + 4)$
$x - 3 = 0$
$x = 3$
And
$x + 4 = 0$
$x = -4$
Once we have successfully factored our equation, we can see that the final solutions to our polynomial graph are: 3 and -4.
[Do take note: though it may look like factoring is a long and involved process, requiring tremendous trial and error, it will become much faster and more instinctual the more you practice with it.]
Just as there are several different types of floofers dogs, there are several different types of polynomial questions. (Perros/Wikimedia)
Typical Polynomial ACT Math Questions
You'll see three main types of polynomial problems on the ACT. These are:
#1: Factoring and FOIL-ing polynomial problems
#2: Graphing polynomial problems
#3: Operations (multiplication, division, addition, or subtraction) of polynomials
Let's look at each of these types of problems in more detail.
Factoring and FOIL-ing Polynomial Problems
These are the most common polynomial problems you'll see on the test. Generally, these problems will ask you to find the two solutions to a quadratic polynomial expression.
To solve these types of problems, you must follow the same process we walked through in the last section on factoring and FOIL-ing. Alternatively, you can also use the strategy of plugging in answers (PIA) if you prefer not to factor and FOIL.
If $2x^2+6x=36$, what are the possible values of $x$?
F. -12 and 3
G. -6 and 3
H. -3 and 6
J. -3 and 12
K. 12 and 15
Solving Method 1: Factoring
To solve this problem, let us first set the equation to zero, so that we can work with the full polynomial expression on one side of the equals sign.
$2x^2 + 6x = 36$
$2x^2 + 6x - 36 = 0$
Now let us set up our parentheticals.
$(2x +/-$ __$)(x +/-$ __$)$
Just by looking at the polynomial in question, we can make an educated guess as to what integer pair will be used to create -36 as their multiple, out of all the possible number pairings. Most likely, the pairing will be -6 and 6 or 6 and -6 (rather than -1 and 36, -2 and 18, -3 and 12, or -4 and 9) and we can see why if we plug them in.
$(2x - 6)(x + 6)$
$2x^2 + 12x - 6x - 36$
$2x^2 + 6x - 36$
This matches our given equation, so we know this must be our proper factored expression. Now we need to finish finding our two solutions by setting each parenthetical to zero.
$2x - 6 = 0$
$2x = 6$
$x = 3$
And
$x + 6 = 0$
$x = -6$
Our final solutions are 3 and -6.
Our final answer is G, -6 and 3.
Again, the more often you work with factoring polynomials, the better your instincts will become at finding the right numbers to fill in your FOIL-ing. But don't despair if your instincts haven't gotten there yet or if you would rather solve the question by plugging in answers instead! Let's take a look at how.
Solving Method 2: Plugging in Answers
If we again take our same polynomial,
$2x^2 + 6x = 36$
We could plug in our answer choices in place of $x$ to see which two solutions fulfill the equation.
If we start with answer choice F, we would get:
$2x^2 + 6x = 36$
$2(-12)^2 + 6(-12) = 36$
$2(144) - 72 = 36$
$216 = 36$
Since this solution is NOT correct, answer choice F cannot be true.
Answer choice G gives us:
$2x^2 + 6x = 36$
$2(-6)^2 + 6(-6) = 36$
$2(36) - 36 = 36$
$72 - 36 = 36$
$36 = 36$
This is correct, but we must also test the second solution to make sure that answer choice G is the final answer. Both solutions must match in order for the answer choice to be correct.
$2(3)^2 + 6(3) = 36$
$2(9) + 18 = 36$
$18 + 18 = 36$
$36 = 36$
Both solutions for $x$ fit our equation. This means that answer choice G (and only answer choice G) is correct.
Again, our final answer is G, -6, 3.
Graphing Polynomial Problems
Sometimes you may be asked to graph polynomials, identify polynomial graphs, or answer questions about given polynomial graphs. To answer these questions, it's a good idea to re-familiarize yourself with the basics of linear graphs and functions, if you haven't already.
We know that the solution(s) of a parabola is measured at the intersection of the parabola with the $x$-axis (when $y = 0$). By looking at this graph, we can see that the parabola hits the $x$-axis at two distinct points—one point where the $x$ value would be negative and one point where the $x$ value would be positive.
Notice that it doesn't actually matter if we know what the values are, just that one is to the left of the $y$-axis and one is to the right of the $y$-axis. (For more on the coordinate plane and its negatives and positives, check out our guide to ACT points).
Our final answer is H, 1 positive real solution and 1 negative real solution.
Polynomial Operations
The final category of polynomial problems you'll see on the test are operations problems involving polynomials. These will most often be located somewhere in the first fifteen or twenty questions on the test and you'll generally be able to solve them just fine if you are familiar with your algebraic operations.
What polynomial must be added to $x^2-2x+6$ so that the sum is $3x^2+7x$?
A. $4x^2+5x+6$
B. $3x^2+9x+6$
C. $3x^2+9x-6$
D. $2x^2+9x-6$
E. $2x^2-5x+6$
Here, we are adding unknown polynomial $a + b + c$ to our given polynomial $x^2 - 2x + 6$ in order to equal $3x^2 + 7x$.
If we know our operations, then we know that like terms can only be combined with like terms. So let us take these polynomials piece by piece.
$x^2 + a = 3x^2$
$a = 2x^2$
We know that our first term must be $2x^2$, so we can eliminate answer choices A, B, and C.
$-2x + b = 7x$
$b = 9x$
We now know that the second term in our polynomial must be $9x$, which means that we can eliminate answer choice E. Even without finishing the problem, we can confidently select answer choice D as the correct answer. But we can also finish up just to make absolutely sure.
$6 + c = 0$
$c = -6$
Once we put our pieces together, we know we must add the polynomial
$2x^2 + 9x - 6$
to our given polynomial in order to equal the polynomial that we want.
Our final answer is D, $2x^2 + 9x - 6$
Now to slot those last few pieces into place and we're all set to go!
Strategies for Solving Polynomial Questions
Though you will see a few different types of polynomial problems on the ACT, there are a few strategies you can use to make solving polynomial problems as a whole a little easier.
Strategy 1: Remember to Review Your Operations and Functions Guides
Operations questions and function questions go hand in hand with polynomial questions, so it's a good idea to keep a close eye on all three math topics and learn how they work together. For instance, it would be difficult to solve your graphing polynomial questions or your operations of polynomials without at least a passing understanding of algebraic operations or functions as a whole.
Strategy 2: Write It Out
It can become very tempting to work with polynomials completely in your head, especially if you're already familiar with polynomials, factoring, and FOIL-ing. But doing this can lead you to make careless errors and select "bait" answer options.
The ACT is a fast paced test and the test-makers know that this kind of time pressure can lead students to start working in their heads to speed up the process. To make the test challenging, polynomial questions often use negatives or large numbers, and so it can be all too easy to fall for a bait answer choice if you do all your polynomial math in your head.
Just remember to take a breath and write your information down as you work through your problems to avoid careless errors such as these, especially when it comes to your positives and negatives.
Strategy 3: Remember to Use PIA When Necessary
If you're not that familiar with factoring polynomial quadratic expressions (or it's just been a long time since you've done it in school) and you're struggling to do so quickly and efficiently, it might be a good idea for you to switch techniques and start using the strategy of plugging in answers to find your solutions instead. It may take a little longer to use this technique, but it will always lead you to the correct solution. So if you've come up against factoring and can't quite manage it for any reason, don't panic—you can absolutely still solve the problem just by using PIA.
Test Your Knowledge
Ready to put your polynomial knowledge to the test? Then let's dive in!
1. Which of the following is a factored form of the expression $5x^2 -13x-6$?
A. $(x-3)(5x+2)$
B. $(x-2)(5x-3)$
C. $(x-2)(5x+3)$
D. $(x+2)(5x-3)$
E. $(x+3)(5x-2)$
2. In the equation $x^2+mx+n=0$, $m$ and $n$ are integers. The only possible value for $x$ is -3. What is the value of $m$?
A. 3
B. -3
C. 6
D. -6
E. 9
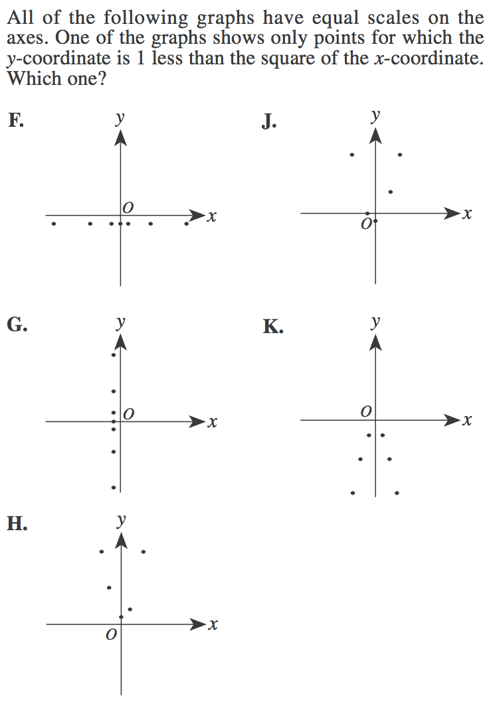
3.
4. What values of $x$ are solutions for $x^2+2x=8$?
A. -4 and 2
B. -2 and 0
C. -2 and 4
D. 0 and 2
E. 6 and 8
Answers: A, C, J, A
Answer Explanations:
1. To solve this problem, we can either factor the polynomial ourselves or we can simply test our answer choices and see which is correct. In this case, let us simply test our answer choices using PIA.
Answer choice A gives us $(x - 3)(5x + 2)$. Let us FOIL this out.
$(x * 5x) + (x * 2) + (-3 * 5x) + (-3 * 2)$
$5x^2 + 2x - 15x - 6$
$5x^2 - 13x - 6$
This is exactly the polynomial we needed to find so luckily for us, we can stop here. We know by the rules of multiple choice that there will only ever be one correct answer, so we know answer choice A will be the one right solution—no need to test any others.
Our final answer is A, $(x - 3)(5x + 2)$.
2. If we remember from our earlier lessons, we know that a factored polynomial will typically have two solutions. For example, if our factoring gives us $(x - 3)(x + 4)$, our final two solutions will be $x - 3 = 0$ => $x = 3$ and $x + 4 = 0$ => $x = -4$. This gives us our two solutions of +3 and -4.
So what does it mean that a polynomial only has one solution? It would mean that our factored polynomial would have to be a square. That way the two solutions would be the same. For example, if we had $(x + 7)(x + 7)$, our only solution would be $x + 7 = 0$ => -7.
So if our polynomial is $x^2 + mx + n = 0$, and our only solution is -3, then we know that our factoring is going to look like:
$(x + 3)(x + 3)$
Why? This gives us our final solution of -3, since $x + 3 = 0$ => $x = -3$.
Now, to find the value of $m$, we need to FOIL back out our factoring.
$(x + 3)(x + 3)$
$(x * x) + (x * 3) + (3 * x) + (3 * 3)$
$x^2 + 3x + 3x + 9$
$x^2 + 6x + 9$
The 6 is now standing in place of our $m$ variable, so our $m = 6$.
Our final answer is C, 6.
3. Though you can set up your own quadratic equation to fit the problem, the easiest way to solve this question is to test out point on your graphs and see which one fits the premise. We are told that the y-coordinate value of any point will be the $x$-coordinate squared minus 1, so let's test each graph.
Graph H is a constant graph. As we saw from constant graphs earlier and as we can see here, the $y$-coordinate value never changes. This means that the $x$-coordinates will increase or decrease, but the $y$-coordinate for any point will NOT be exactly 1 less than the $x$-coordinate squared. We can eliminate graph H.
For the same reason, we can eliminate graph G; the $x$-coordinate value never changes even as the $y$-coordinate value does. This does not fit our criteria.
We can also eliminate graph K, as it would be impossible for such a parabola to open downwards. If the $x$-coordinates values were negative, then anything smaller than -1 (say -2) would result in a positive y-coordinate value, according to our rules. For instance, if $x$ were -2, then y would be: $-2^2 - 1 = 3$.
So we are left with two graphs—J and H—both which look promising for the moment. Let us test some values for them.
In graph J, we can roughly estimate a few points to be $(0, -1)$, $(-1, 0)$ and perhaps roughly $(2, 3)$. If we go off our premise of $y = x^2 - 1$, then all of these points fits our criteria.
$0^2 - 1 = -1$
$-1^2 - 1 = 0$
$2^2 - 1 = 3$
It's pretty certain that J is our right answer, but since we were estimating our points, it's a good idea to rule out graph H if we can.
We can roughly estimate three of the points on graph H to be: $(0, 1)$, $(2, 2)$ and perhaps $(-2, 5)$. None of these match our criteria.
$0^2 - 1 ≠ 1$
$2^2 - 1 ≠ 2$
$-2^2 - 1 ≠ 5$
We have confirmed that graph J is indeed correct.
Our final answer is J.
4. Here we have another problem that we can either factor ourselves or use PIA for. This time, let us factor.
First, we need to bring everything to one side of the equals sign, so let us subtract both sides by 8.
$x^2 + 2x - 8 = 0$
Now, we can factor. We know we need two numbers multiplied together to equal -8, so one of them must be a negative. These numbers must also add together to equal +2, so our likely pairing will be +4 and -2. Let us test it out to be sure.
$(x + 4)(x - 2)$
$(x * x) + (x * -2) + (4 * x) + (4 * -2)$
$x^2 - 2x + 4x - 8$
$x^2 + 2x - 8$
Perfect, we've found our factors! Now we just need to set each to zero to find our final solutions.
$x + 4 = 0$
$x = -4$
And
$x - 2 = 0$
$x = 2$
Our final answer is A, -4 and 2.
Whoo, you did it! No need to toot your own horn, we'll do it for you—congrats!
The Take-Aways
Polynomial questions can sometimes be tricky, but a solid understanding of functions and operations can help you tremendously when it comes to understanding how to visualize and manipulate your polynomial expressions.
Just remember to not underestimate the value of keeping track of your positive and negative signs and you'll be knocking out a not-insignificant chunk of your ACT math section in no time.
What's Next?
Now that you've taken on polynomials (and no doubt rocked them), you might want to take a look at our other ACT math guides for any individual math topic you could need. From ratios to rotations, points to probabilities, we've got your covered.
Running into some snags with your FOILing and factoring? You might want to review the distributive property and perfect squares.
What does it mean to complete the square and how is that relevant to polynomials and factoring? Learn about completing the square and when you'll need to use it here.
Stuck on an ACT math problem? Whether you're stuck on a study guide, a practice test, or you just want to know how to get yourself out of a math bind on test day, don't sweat it. We'll show you how to figure our when you're really stuck and what to do about it.
Want to make sure you're really prepared for test day? We've gathered together the best ACT math resources available and compiled them into one ultimate ACT math study guide. No more hunting for tips and resources—they're available at your fingertips in one easy place.
