The SAT doesn't give any penalties for incorrect answers, so you should always guess on a section, including the Math section. But guessing requires strategy, especially if you're hoping to get a high (or even perfect!) SAT Math score.
In this guide, we’ll go through how to guess strategically on SAT Math and show you examples of it in action.
Refresher: SAT Math Scoring and Organization
The SAT is a standardized test, which means that each SAT must look and feel like every other SAT as much as possible. The individual questions may vary, but the patterns in how the College Board designs both the questions and their answer choices will be as similar as can be.
With time and practice, you'll learn to not only recognize these patterns when you see them, but also to use the clues in both the question and answer choices to help you find your right answer (or at least narrow down your options).
Now then, let's refresh your understanding of exactly how the SAT Math section is scored.
For each question you answer correctly, you get 1 (raw) point. You neither lose nor gain points for incorrect or blank answers. So your total raw Math score is simply the number of questions you got right out of 58, as there are 58 total questions (20 on No Calculator and 38 on Calculator).
This raw score is then converted into a final Math score on a scale of 200-800 through a process called equating. The exact raw score you'll need to get a specific scaled score for SAT Math will vary somewhat depending on the SAT you take, since each SAT has different questions and thus slightly different difficulty levels.
Finding Your SAT Baseline and Target Scores
While the SAT doesn't give out any penalties for wrong or blank answers, your strategy for how to approach the Math section will vary slightly depending on your target score.
But first, you'll want to find your baseline score, that is, the score you start with before beginning any SAT prep. You can do this by taking an official practice test. As you take this test, make sure to use official time constraints so that you can get an accurate baseline score in the end.
In addition, come up with different ways to mark the Math questions—one mark for questions you don't know how to do, and another mark for questions you're only somewhat confident about. You might even want to create a third marker for questions you know how to do but that will take a long time or will require multiple steps and thus must be done carefully to avoid errors.
For now, just use your best judgment on whether to temporarily skip or guess the questions you've marked, but do make sure you can identify which problems were which later on while scoring your test. These marks will help you when you go to analyze your answers (and of course your guessing strategy) in the next section.
Ultimately, make sure to put down an answer for all SAT questions, even if you have no clue how to approach some. You're not going to lose any points for wrong or skipped answers, so you should always have something put down!
Once you're done with your practice test, check out our guide on how to develop your ideal target score based on your current SAT scores and the schools you want to get into.
Don't worry if you're slightly off your target right now. A little strategy and practice will soon get you much closer to where you want to be (if not right on the bullseye!).
Guessing Based on Your SAT Target Score
After you've figured out your target SAT score, you'll want to see how that translates to your raw score. In other words, how many questions must you answer correctly to reach your target score?
Keep this number in your head and then plan to answer a few more questions than that. This lets you have a buffer, or room to get a few questions wrong.
For example, if your target SAT Math score is 600, you’ll need a raw score of about 38. To earn this raw score, you must answer 38 questions correctly. But this can be difficult, so aim to get right somewhere in the range of 44 questions. This would allow you to miss up to six questions and still get that raw score you need of 38.
Once you’ve scored your practice SAT, look back at all the Math questions you marked. How accurate is your guessing right now? For the Math questions you marked as "didn't know" or "kind of knew," did you mostly get them right or wrong? Is there a pattern in your missed guesses? Think about how your approach is working (or not working) based on the raw score you got and the raw score you actually need.
But what happens if you're well under your target raw score? If this is the case, then you're going to want to establish a two-tonged study approach of brushing up on the individual math topics you're struggling with right now and learning how to guess more effectively.
Now that you’ve seen how you’re guessing strategies have worked so far (even if that means you haven't been guessing at all), let’s talk best guessing strategies for SAT Math.
The more you practice, the more refined and honed your study skills and guessing abilities will become.
4 Essential SAT Math Guessing Strategies
The SAT Math section is designed to test how well you can recognize and figure out how to apply various math concepts to new situations. While the scenarios might be unusual, each and every math topic on the test is one that you're likely familiar with and have studied for years.
This is all to say that you probably have a better understanding of the questions than you might think, even if you don’t know how to actually solve the problems. Often (though not always), a little strategy will allow you to eliminate at least one or two answer choices and make an educated guess.
Note: This might seem apparent, but only use your guessing strategies when you don't know how to solve a problem or are not confident about your answer. Guessing usually takes a little more time than a straight-solve, so if you know the answer, great—now move on to the next problem. Only stop and take the time to guess if you're really stuck.
We’ve laid out four of the most important rules of thumb that go into making an educated guess on an SAT Math problem. Most of the time, you'll use a combination of these four techniques on any given math problem, so they're less individual strategies than they are a combination of thought processes you should go through every time you make a guess.
SAT Math Guessing Strategy 1: Process of Elimination
Being able to eliminate answer choices is arguably a far more important skill than even being able to solve questions (or at least equally as important). Most SAT Math questions are multiple choice, so the correct answer will always be there among the four answer choices.
This might seem obvious, but what this means is that you essentially have two options for getting to the answer: you can solve the problem for the correct answer, or you can eliminate three wrong answers. Whatever remains must be correct. Either option will get you to the right answer in the end.
For example, is it impossible that the answer to a particular problem is negative? Or do you know that a parabola must open upward, even if you don't know how it's positioned horizontally? Even understanding just a tiny bit about the math problem or its possible answer will often be enough to allow you to eliminate a couple answer choices.
But what if don't know enough about a problem to know that three answers are wrong? Is eliminating just one or two answer choices enough to justify a totally random guess?
Eliminating 0 Answer Choices
So you’ve come to a math question and you can’t eliminate any answer choices at all—should you guess? Well, yes—you won't lose any points for random guessing—but just realize there's not a super-high chance you'll get it right.
Still, you never know! So just mark an answer choice and call it a day. It can also be helpful to have a guessing letter picked out ahead of time. This means that in the event you have no idea how to answer an SAT Math question (and you're running out of time to do some proper guesswork), you can simply mark the letter you've decided on as your guessing letter (A, B, C, or D) and move on.
Eliminating 1 Answer Choice
Let’s say you can eliminate one answer choice but no others. This means you'll have a 33% chance of getting the right answer. That's definitely (slightly) better than the 25% chance you have if you were to just blindly guess on a question—but it's still lower than what you want it to be.
In this case, you can either use your guessing letter (see above) or look through the answer choices and see whether any in particular stand out to you or feel right. Obviously, don't use your guessing letter if that's the choice you've managed to peg as the clearly wrong answer!
Eliminating 2 Answer Choices (Now We’re Getting Somewhere!)
If you can eliminate two answer choices, you’re in a great place! This will give you a one-in-two shot of choosing the correct answer.
Eliminating 3 Answer Choices
If you can confidently eliminate three answer options, then celebrate! No need for guessing here—you’ve found the correct answer.
Now, how exactly do you go about eliminating answer choices? Let’s take a look.
Up next, we'll learn how approximating on SAT Math can help you narrow down your answer choices.
SAT Math Guessing Strategy 2: Approximating
If you have even a general idea of what the right answer might be (even a ballpark figure will do), you'll often be able to eliminate one or two of the most blatant outliers. Though the answer choices are most often generated based on common student errors or closely tied values, there will still generally be answer choices that are way far afield.
Let’s take a look at this in action. Don’t worry about actually solving the math problem—just give yourself enough of a ballpark to see whether you can eliminate one or two answer choices.
Katarina is a botanist studying the production of pears by two types of pear trees. She noticed that Type A trees produced 20 percent more pears than Type B trees did Based on Katarina's observation, if the Type A trees produced 144 pears, how many pears did the Type B trees produce?
A) 115
B) 120
C) 124
D) 173
Here, we're told that Type A trees produced 20% more pears than Type B trees did.
We're also told that Type A trees produced a total of 144 pears, which means Type B trees must have produced fewer than 144 pears, but not by that much—just 20%.
With this approximation alone, we can immediately eliminate answer choice D (173 pears), giving us a one-in-three chance of getting the right answer.
Note: The correct answer is B: 120.
You can also approximate answers on diagrams on the test. Unless otherwise noted, all figures will be drawn to scale, and you can make a ballpark guess as to their sizes and angles.
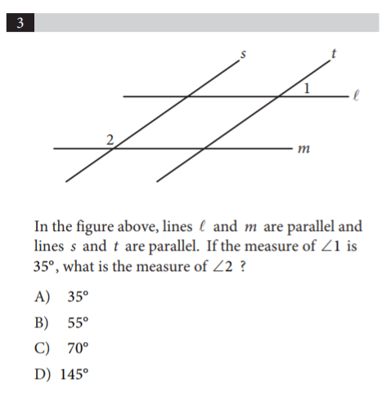
Without even worrying about the context of the problem, we can tell right away that ∠2 is larger than ∠1, which equals 35°.
We can also tell that ∠2, based on the way it's been drawn for this figure, is clearly an obtuse angle, meaning it's larger than a right angle. In other words, ∠2 must be bigger than 90°.
As a result, we can immediately eliminate answer choices A, B, and C, which are all less than 90°. This leaves us with answer choice D: 145° as the correct solution.
The more you can whittle away obviously wrong answers, the better the odds will be of you grabbing that right answer choice.
SAT Math Guessing Strategy 3: Plugging In Answers
This strategy is one of the most useful for narrowing down your answer choices for problems on SAT Math.
Basically, all it entails is going through the four answer choices and plugging in each answer to the problem to see which one results in the correct solution (and which ones don't). You should consider using this approach when faced with tricky algebra or if you want to check your answer.
This strategy is best used after you've given yourself a chance to do some approximating for the answer (see strategy above) and have a clearer idea of the type of answer you're looking for and the types of answers you're definitely not looking for.
Always start with answer choice B or C when plugging in. Doing this tells you whether you'll need to work your way up to higher values (answer choices C and D) or work your way down to lower values (answer choices A and B).
Let's look at some examples of how this strategy works on SAT Math.
If ${x-1}/3=k$ and $k=3$, what is the value of $x$?
A) 2
B) 4
C) 9
D) 10
This SAT Math question is a pretty basic algebra problem. But if you're not confident in your algebra skills or simply want to check that the answer you've chosen is indeed right, you can go ahead and plug in answers.
Let's start with answer choice B. By plugging in 4 to the equation provided (and 3 for $k$), we get this as our answer:
${4-1}/3=3$
$3/3=3$
$1≠3$
Clearly, 1 does not equal 3, so answer choice B is definitely wrong. Because 1—the solution when using choice B—is less than 3, we know that $x$ will have to be larger than 4. So let's work our way up with answer choice C.
By plugging in 9 to the equation, we get this:
${9-1}/3=3$
$8/3=3$
$2.67≠3$
As you can see, we're getting closer to 3 but still aren't quite there. This means that answer choice D, which is the highest possible value of $x$, must be correct. Just to be sure, though, let's run through the equation one last time, this time with $x$ equaling 10:
${10-1}/3=3$
$9/3=3$
$3=3$
This result confirms that the correct answer to this problem is answer choice D: 10.
Here's another example of plugging in answers:
$$ℓ=24+3.5m$$
One end of a spring is attached to a ceiling. When an object of mass $m$ kilograms is attached to the other end of the spring, the spring stretches to a length of $ℓ$ centimeters as shown in the equation above. What is $m$ when $ℓ$ is 73?
A) 14
B) 27.7
C) 73
D) 279.5
Here, we're being asked to solve for $m$ when $ℓ=73$. This means our equation looks like this:
$73=24+3.5m$
Just glancing at the answer choices, we can see that there's a pretty big range of numbers, with D (279.5) clearly being an outlier and likely an incorrect answer. So let's eliminate D.
This gives us three answer choices to choose from: A, B, or C. When we start to plug in answers, we'll begin with the middle value, or answer choice B. Here's what we get when we plug in 27.7 for $m$:
$73=24+3.5{(27.7)}$
$73=24+96.95$
$73≠120.95$
Evidently, B is not the right answer—it's way too high! This means we'll need to look at even smaller numbers, and there's just one answer choice that meets this requirement: A.
At this point, you could go ahead and mark A as correct and move on. But it's a smart idea to check your work if you can, so let's quickly plug in 14 to confirm that A is indeed the solution:
$73=24+3.5{(14)}$
$73=24+49$
$73=73$
Just as we predicted, the correct answer is A: 14.
Our final SAT Math guessing strategy is all about learning to resist temptation.
SAT Math Guessing Strategy 4: Avoiding Temptation
The test is designed around the statistically average student, so many of the answer choices are generated based on common student errors. People have a tendency to fall into predictable thinking patterns, and the SAT is, in part, designed to lure you to fall for traps that the average student falls for again and again.
Often, what makes an answer difficult is the wording and the bait answer choices, rather than the difficulty of the mathematical material being tested. So if you look at a question in the medium or difficult range that looks easy or—even worse—obvious, it might just be too good to be true.
If an answer choice seems immediately appealing, especially on a more difficult question, it’s likely a trap. Think about how many other students would have felt the same way on trial tests. Don’t be that person, and try not to let yourself fall for the booby traps!
When 4 times the number $x$ is added to 12, the result is 8. What number results when 2 times $x$ is added to 7?
A) -1
B) 5
C) 8
D) 9
This question is a good example of the types of traps you'll see on SAT Math.
The problem tells us, "When 4 times the number $x$ is added to 12, the result is 8." Obviously, when something is added to 12 and the result is a number that's less than 12, that number must be a negative. And anything multiplied by a negative is also a negative, so $x$, as far as we know, has to be a negative number.
You might be tempted to immediately select answer choice A, since this is the only choice that's a negative number. But not so fast! Reread the problem and you'll see that what we're actually solving for is a different variable (we'll call it $y$).
Therefore, the answer choice is most likely not $-1$—this is just a trick answer choice meant to make us think we need to solve for $x$ and not $y$.
Now, you have three answer choices left—B, C, and D—from which you can venture a guess.
Note: The correct answer is B: 5.
Let's take a look at another example of an SAT Math problem that's trying to throw you off:
Last week Raul worked 11 more hours than Angelica. If they worked a combined total of 59 hours, how many hours did Angelica work last week?
A) 24
B) 35
C) 40
D) 48
At a glance, this problem doesn't look that hard. We know that Raul worked 11 more hours than Angelica did and that, together, they worked a total of 59 hours.
With these two numbers in your head, you're probably tempted to choose answer choice D (48 hours), since $59-11=48$.
But this is a trap! If you chose D, you'd be saying that Raul only worked 11 hours overall and that Angelica worked 48 hours—which doesn't make any sense, as Raul worked more than Angelica did.
So right away, you can cross off D to narrow down your possible answers to A, B, or C.
Note: The correct answer is A: 24.
You did it! Now go forth and conquer.
Key Takeaways: Guessing Strategically on SAT Math
Although it's useful to know how to actually solve SAT Math problems, it's not always necessary. You shouldn’t guess on every math question, of course, but knowing how to guess effectively can raise your chance of getting the score you want on test day.
Just remember to always employ your guessing strategies whenever you're not sure how to answer a question and take a deep breath. Sometimes you'll be able to eliminate enough answer choices to make a really good guess, while other times you'll have to venture a completely random guess—and that's perfectly OK! You won't lose any points for wrong answers, so don't be afraid to take the plunge and guess.
Truth be told, you probably know more about the math topic in question than you think, and you likely know enough to eliminate at least one answer choice, even if you’re feeling overwhelmed.
Don’t doubt your skills to eliminate possible answer choices. Pretty soon you’ll be beating the odds and boosting your SAT Math score more than ever before!
What’s Next?
Still not satisfied with your SAT Math scores? Improve your SAT Math topic skills by working through our individual math topic guides. We walk you through the definition of each topic, the formulas you'll need, and how you'll see the questions on the SAT.
Been procrastinating on your SAT prep? If you've found yourself in a study rut, check out our guide on how to stop procrastinating so you can get back on that study wagon.
Aiming for a perfect score? If you're looking to score a perfect 800 on SAT Math, then look no further than our guide to getting an 800 on the Math section, written by a real full scorer.
