
Are you scoring in the 26-34 range on ACT Math? Do you want to raise that score as high as possible—to a perfect 36?
Getting to a 36 ACT Math score isn't easy. It'll require perfection. But with hard work and my strategies below, you'll be able to do it. I've scored 36 on Math on all my ACTs, and I know what it takes. Follow my advice, and you'll get a perfect score—or get very close.
Brief note: This article is suited for students already scoring a 26 on ACT math or above. If you're below this range, my "How to improve your ACT Math score" article is more appropriate for you. Follow the advice in that article, then come back to this one when you've reached a 26.
Overview
In this article, I'm going to discuss why scoring a 36 is a good idea, what it takes to score a 36, and then go into the 8 key ACT Math strategies so you know how to get a 36 on ACT Math.
Stick with me—as an advanced student, you probably already know that scoring high is good. But it's important to know why a 36 Math score is useful, since this will fuel your motivation to get a high score. Then we'll get into the meat of the article.
Finally, in this guide, I talk mainly about getting to a 36. But if your goal is a 32, these strategies still equally apply.
Understand the Stakes: Why a 36 ACT Math?
Let's make something clear: for all intents and purposes, a 34 on an ACT is equivalent to a perfect 36. No top college is going to give you more credit for a 36 than a 34. You've already crossed their score threshold, and whether you get in now depends on the rest of your application.
So if you're already scoring a 34, don't waste your time studying trying to get a 36. You're already set for the top colleges, and it's time to work on the rest of your application.
But if you're scoring a 33 or below AND you want to go to a top 10 college, it's worth your time to push your score up to a 34 or above. There's a big difference between a 32 and a 34, largely because it's easy to get a 32 (and a lot more applicants do) and a lot harder to get a 34.
A 33 places you right around average at Harvard and Princeton, and being average is bad in terms of these top schools, since their admissions rates are typically below 10%.
So why get a 36 on ACT Math? Because it helps you compensate for weaknesses in other sections. By and large, schools consider your ACT composite score much more important than your individual section scores. If you can get a 36 in ACT Math, that gives you more flexibility in your English and Reading scores. It can compensate for a 32 in one other section, for example, to bring your average back up to 34.

There are two other scenarios where a 36 in ACT Math is really important. First is if you're planning for a quantitative or science major (like math, physics, statistics, chemistry). The second is if you're applying to a highly selective technical school like MIT or Caltech.
Here's the reason: college admissions is all about comparisons between applicants. The school wants to admit the best, and you're competing with other people in the same "bucket" as you.
By applying as a math/science major, you're competing against other math/science folks: people for whom ACT Math is easy. Really easy.
Even though schools don't typically release their ACT scores by section, they do release SAT section scores, so we can take a look at SAT Math scores at top schools. Here are a few examples from schools. For Harvard, Princeton, MIT, and Caltech, the 75th percentile SAT Math score is an 800 (or equivalent to an ACT 36). That means at least 25% of all students at these schools have an 800 in SAT Math, or a 36 on ACT Math.
Even more surprising: the 25th percentile score for SAT Math at both MIT and Caltech is 790, or a 35 on the ACT! This means if you score anything other than a 36 on ACT Math, you're well below average for these schools!
I'm not going to lie. ACT Math was super easy for me. I got 36 on pretty much every practice test and official ACT I ever took. This was largely because I had a strong math background and competed in math competitions like AMC/AIME. I also worked hard and applied the strategies below to achieve perfection.
You're competing against people like me. And if you apply with a 34 or below on Math, schools like MIT, Harvard, and Princeton are going to doubt your ability. Because ACT Math is supposed to be trivially easy for you.
But if you can work your way to a 36, you show that you're at an equal level (at least on this metric). Even if it takes you a ton of work, all that matters is the score you achieve at the end.

Know That You Can Do It
This isn't just some fuzzy feel-good message you see on the back of a Starbucks cup.
I mean, literally, you and every other reasonably intelligent student can score a 36 on ACT Math.
The reason most people don't is they don't try hard enough or they don't study the right way.
Even if math wasn't your strongest suit, or you got a B+ in Calculus, you're capable of this.
Because I know that more than anything else, your ACT score is a reflection of how hard you work and how smartly you study.
Here's why: the ACT is a weird test. When you take it, don't you get the sense that many questions are nothing like what you've seen in school?
It's purposely designed this way. The ACT can't test difficult concepts, because this would be unfair for students who never took AP Calculus. It can't ask you to solve Fermat's Last Theorem. The ACT is a national test, which means it needs a level playing field for all students around the country.
So it HAS to test concepts that all high school students will cover. Numbers (integers, fractions, ratios), Algebra (solving equations for x, word problems), Geometry (x-y coordinate geometry, circles squares and triangles), Trigonometry, Probability.
You've learned all of this before in high school.
But if all the questions were easy and straightforward, then everyone would score too high. So the ACT needs to test these concepts in strange ways. This trips up students who don't prepare, but it rewards students who understand the test well.
Here's an example:
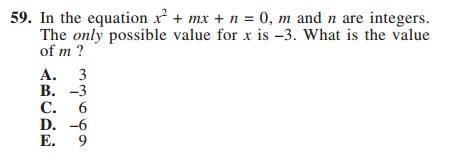
This is one of the more difficult problems in ACT Math. You might already know how to solve it. But it's unlikely you ever ran into something like this in school.
Finish trying the question? Did you get stuck?
Most students try to solve this question by plugging in -3 for x. "If the only possible value for x is -3, then plugging it in makes sense, right?"
There's a problem: You can't solve for two variables (m and n) with only one equation.
Here's the way to solve this question. It requires integrating multiple concepts together.
First, this is a critical clue: "the ONLY possible value for x is -3." Normally when you solve a quadratic equation, you get two different values. For example, x2 + 5x + 6 = 0 factors to (x + 2)(x + 3) = 0. This gives you two values for x, -2 and -3.
But this question is telling us that when you factor the equation, you get -3 for both values of x.
If x = -3, then x + 3 = 0. Getting (x + 3) twice means squaring (x + 3). This gives us:
(x + 3)2 = 0
x2 + 6x + 9 = 0
So the answer to this question is C, m = 6
This question is difficult for many students because you're not trained to think about factoring in this way. If the ACT merely asked you, "what is the value of x if x2 + 6x + 9 = 0?" most students would be able to answer this easily. This is what you did in school.
But in this weird format, it's easy to get tripped up. If you don't make the connection that I showed above, it's very hard for you to solve this question.
The ACT math section is full of weird examples like this, some of which get even more difficult.
But the next time you see a question like this, you already know the trick—and you know exactly what to do.
Therefore, to improve your ACT Math score, you just need to:
- master the types of questions that the ACT tests, like the one above
- draw on the correct concepts you already know to solve the questions
- practice on a lot of questions so you learn from your mistakes
I'll go into more detail about exactly how to do this. First, let's see how many questions you need to get right a 36.
What It Takes to Get a 36 in Math
If we have a target score in mind, it helps to understand what you need to get that score on the actual test.
Here's a sample raw score to ACT Math Score conversion table. (If you could use a refresher on how the ACT is scored and how raw scores are calculated, read this.)
| Scaled Score | Math Raw Score |
| 36 | 40-41 |
| 35 | 39 |
| 34 | 37-38 |
| 33 | 36 |
| 32 | 35 |
| 31 | 34 |
| 30 | 33 |
| 29 | 31-32 |
| 28 | 30 |
In all of the currently available Enhanced ACT grading scales, you can miss one scored question and still get a 36 but in past tests you had to get every question to reach a 36—missing 1 would bring you down to an 35. You can also miss all of the 4 experimental questions without lowering your score, but you won't know which questions are unscored.
As such, the safest thing to do is to aim for perfection. On every practice test, you need to aim for a perfect raw score for a 36.
As a final example, here's a screenshot from my exact score report showing that I missed 1 question (oops) and earned a 36.


OK—so we've covered why scoring a higher ACT math score is important, why you specifically are capable of improving your score, and the raw score you need to get to your target.
Now we'll actually get into actionable strategies that you should use in your own studying to maximize your score improvement.
Strategies to Get a 36 on ACT Math

Strategy 1: Understand Your High Level Weakness — Content or Time Management?
Every student has different flaws in ACT Math. Some people aren't comfortable with the underlying math material. Others know the math material well, but can't solve questions quickly enough in the harsh time limit.
(As we'll discuss, the ACT Math section applies heavy time pressure. So you likely do suffer from some time pressure—we're trying to figure out how much)
Here's how you can figure out which one applies more to you:
- Take only the math section of a practice test. We have the complete list of free practice tests here.
- For that section, use a timer for 50 minutes. Treat it like a real test.
- If time runs out and you're not done yet, keep working for as long as you need. But starting now, for every new answer or answer that you change, mark it with a special note as "Extra Time."
- Grade your test using the answer key and score chart, but we want two scores: 1) The Realistic score you got under normal timing conditions, 2) The Extra Time score. This is why you marked the questions you answered or changed during Extra Time.
Get what we're doing here? By marking which questions you did under Extra Time, we can figure out what score you got if you were given all the time you needed. This will help us figure out where your weaknesses lie.
If you didn't take any extra time, then your Extra Time score is the same as your Realistic score.
Here's a flowchart to help you figure this out:
Was your Extra Time score a 32 or above?
If NO (Extra Time score < 32), then you have remaining content weaknesses. You might have weaknesses across a range of subjects, or a deep weakness in only a few subjects. (We'll cover this later). Your first plan of attack should be to develop more comfort with all ACT Math subjects.
If YES (Extra Time score > 32), then:
Was your Realistic score a 32 or above?
If NO (Extra Time score > 32, Realistic < 32), then that means you have a difference between your Extra Time score and your Realistic score. If this difference is more than 2 points, then you have some big problems with time management. We need to figure out why this is. Are you generally slow at math across most questions? Or did particular problems slow you down? Generally, doing a lot of practice questions and learning the most efficient solutions will help reduce your time. More on this later.
If YES (both Extra Time and Realistic scores > 32), then you have a really good shot at getting a 36. Compare your Extra Time and Realistic score—if they differed by more than 1 point, then you would benefit from learning how to solve questions more quickly. If not, then you likely can benefit from shoring up on your last content weaknesses and avoiding careless mistakes (more on this strategy later).
Hopefully that makes sense. Typically I see that students have both timing and content issues, but you might find that one is much more dominant for you than the other. For example, if you can get a 36 with extra time, but score a 32 in regular time, you know exactly that you need to work on time management to get a 36.

Strategy 2: Do a Ton of Practice, and Understand Every Single Mistake
On the path to perfection, you need to make sure every single one of your weak points is covered. Even one mistake on all of ACT Math will knock you down from a 36.
The first step is simply to do a ton of practice. If you're studying from free materials or from books, you have access to a lot of practice questions in bulk. As part of our PrepScholar program, we have over 2,800 ACT questions customized to each skill.
The second step—and the more important part—is to be ruthless about understanding your mistakes.
Every mistake you make on a test happens for a reason. If you don't understand exactly why you missed that question, you will make that mistake over and over again.
I've seen students who have completed 10 practice tests. They've solved over 1,000 math questions, but they're still nowhere near a 36 on ACT Math.
Why? They never understood their mistakes. They just hit their heads against the wall over and over again.
Think of yourself as an exterminator, and your mistakes are cockroaches. You need to eliminate every single one—and find the source of each one—or else the restaurant you work for will be shut down.
Here's what you need to do:
- on every practice test or question set that you take, mark every question that you're even 20% unsure about
- when you grade your test or quiz, review every single question that you marked, and every incorrect question. This way even if you guessed a question correctly, you'll make sure to review it.
- in a notebook, write down the gist of the question, why you missed it, and what you'll do to avoid that mistake in the future. Have separate sections by subject and sub-topic (number theory—fractions, algebra—solving equations, etc.)
It's not enough to just think about it and move on. It's not enough to just read the answer explanation. You have to think hard about why you specifically failed on this question.
By taking this structured approach to your mistakes, you'll now have a running log of every question you missed, and your reflection on why.

No excuses when it comes to your mistakes.
Always Go Deeper—WHY Did You Miss a Math Question?
Now, what are some common reasons that you missed a question? Don't just say, "I didn't get this question right." That's a cop out.
Always take it one step further—what specifically did you miss, and what do you have to improve in the future?
Here are some examples of common reasons you miss a question, and how you take the analysis one step further:
Content: I didn't learn the skill or knowledge needed to answer this question.
One step further: What specific skill do I need to learn, and how will I learn this skill?
Incorrect Approach: I knew the content, but I didn't know how to approach this question.
One step further: How do I solve the question? How will I solve questions like this in the future?
Careless Error: I misread what the question was asking for or solved for the wrong thing.
One step further: Why did I misread the question? What should I do in the future to avoid this?
Get the idea? You're really digging into understanding why you're missing questions.
Yes, this is hard, and it's draining, and it takes work. That's why most students who study ineffectively don't improve.
But you're different. Just by reading this guide, you're already proving that you care more than other students. And if you apply these principles and analyze your mistakes, you'll improve more than other students too.
Strategy 3: If You Have Content Gaps, Be Ruthless About Filling Them
Within ACT Math, you have to master a lot of subjects. At the high level, you need to know number operations, algebra, geometry, trigonometry, probability, and more. Even within each subject, you have subskills to master. Within algebra, you need to know how to solve equations, how to deal with word problems, properties of functions, etc.
Unless you're a math whiz and are already scoring a 34-36, it's unlikely that you've mastered all of these evenly. You probably have different strengths and weaknesses across these subjects.
If from the analysis of mistakes above you find that you have a content problem, you need to improve your understanding of that content.
By Content problem, I mean that you're not comfortable with the underlying math concepts in a subject. Maybe you forgot how to solve a type of problem, or you forgot a formula to use, or you just don't remember the subject material.
If you've identified one of these issues, you've spotted an opportunity for yourself to improve your score.

Fill in the potholes of your understanding.
Think of a mistake like discovering a cavity in your mouth. When your dentist fills in a cavity, he doesn't just patch up the hole right away. He cleans out the entire cavity, sterilizes it, then adds a filling.
Content mistakes are similar—you have a weakness in a subject, say x-y coordinate geometry. This probably means you have a lot of other weaknesses in that subject, beyond the one identified by that question. Don't just focus on understanding that one question you missed.
Take the opportunity to research that subject and get more practice in it. You need to find a way to get lesson material to teach yourself the main concepts that you're forgetting. Then you need to find more practice questions for this skill so you can drill your mistakes.
In our ACT prep program PrepScholar, we do that work for you by splitting up our 2,800+ practice questions by skill and difficulty. If you're weak in algebra—solving equations, you get 20+ questions in a quiz dealing specifically with that skill. This repetitive practice fills up your content gap far better than any other method I know.
Strategy 4: If You Miss a Question, Try It Again Before Reading the Explanation
When you're doing practice questions, the first thing you probably do is read the answer explanation and at most reflect on it a little.
This is a little too easy. I consider this passive learning—you're not actively engaging with the mistake you made.
Instead, try something different—find the correct answer choice (A-E), but don't look at the explanation. Instead, try to resolve the question once over again and try to get the correct answer.
This will often be hard. You couldn't solve it the first time, so why could you solve it the second time around?
But this time, with less time pressure, you might spot a new strategy, or something else will pop up. Something will just "click" for you.
When this happens, what you learned will stick with you for 20 times longer than if you just read an answer explanation. I know this from personal experience. Because you've struggled with it and reached a breakthrough, you retain that information far better than if you just passively absorbed the information.
It's too easy to just read an answer explanation and have it go in one ear and out the other. You won't actually learn from your mistake, and you'll make that mistake over and over again.
Treat each wrong question like a puzzle. Struggle with each wrong answer for up to 10 minutes. Only then if you don't get it should you read the answer explanation.

Strategy 5: Finish With Extra Time and Double Check
Your goal at the end of all this work is to get so good at ACT Math that you solve every question and have extra time left over at the end of the section to recheck your work.
I'll admit, this is hard for the ACT. You have 50 minutes to solve 45 questions, which of course gives an average of just over a minute per question. But the last, most difficult questions might take you 2 or 3 minutes each.
In high school and even now, I could finish the old 60 minute sections in 40 minutes or less. I then had 20 minutes left over to recheck my answers at least once.
The best way to get faster is, as explained above, to do so many questions and get so fluent at the questions that the ways to solve the question become obvious to you. Complicated circle questions become as easy for you as 2+2.
What's the best way to doublecheck your work? I have a reliable method that I follow:
- Try to resolve the question another way. If I solved a question algebraically, I can recheck it by plugging in the solution.
- If I'm 100% sure I'm right on a question, I mark it as such and never look at it again. If I'm not sure, I'll come back to it on the third pass.
- At least 2 minutes before time's up, I rapidly doublecheck that I entered the answers correctly.
If you notice yourself spending more than 30 seconds on a problem and aren't clear how you'll get to the answer, skip and go to the next question. Even though you need a perfect raw score for a 36, don't be afraid to skip. You can come back to it later, and for now it's more important to get as many points as possible.

Paper ACT Tip: Bubbling Answers
Here's a bubbling tip that will save you 4 minutes on the paper version of the exam.
When I first started test taking in high school, I did what many students do: after I finished one question, I went to the bubble sheet and filled it in. Then I solved the next question. Finish question 1, bubble in answer 1. Finish question 2, bubble in answer 2. And so forth.
This actually wastes a lot of time. You're distracting yourself between two distinct tasks—solving questions, and bubbling in answers. This costs you time in both mental switching costs and in physically moving your hand and eyes to different areas of the test.
Here's a better method: solve all your questions first in the book, then bubble all of them in at once.
This has several huge advantages: you focus on each task one at a time, rather than switching between two different tasks. You also eliminate careless entry errors, like if you skip question 7 and bubble in question 8's answer into question 7's slot.
By saving just 5 seconds per question, you get back 225 seconds on the 45 questions. This is huge.
Note: If you use this strategy, you should already be finishing the section with ample extra time to spare. Otherwise, you might run out of time before you have the chance to bubble in the answer choices all at once.

Strategy 6: Eliminate Careless Mistakes
Careless mistakes are one of the most frustrating types of errors to make, and nearly everyone makes them.
You know the underlying material, you know how to solve the question, and you're feeling good. But then you grade the quiz, and you find a careless mistake.
Oops—the question asked for the perimeter of the circle and not the area, which is what you calculated.
These types of errors are the most costly and frustrating. You've already put in a ton of work to master the underlying material, and here a question has tricked you into losing a point.
This is why finishing the test early, like I mention above, is so helpful. You get extra time to take a breather and doublecheck your answers.
If you find that careless mistakes are a recurring problem for you, here are some strategies to get rid of them:
- In the question, underline what the question is specifically asking you to solve for. It's so easy for the ACT to trick you into solving the wrong thing.
- If you're solving for a particular value (like length, area, etc), write the units down in the scratch space.
- Be careful with calculator entry. A missing parentheses makes a big difference. "4 + 9 / 2" is completely different from "(4 + 9) / 2"
- Avoid bubbling errors by using the tip above or taking the digital ACT.
Here's an example:
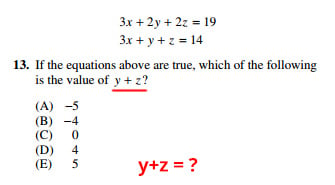
This question is asking us to solve for y + z. Not x, y, or any other combination of variables.
To make sure I remember this, I underline y + z, and I also write "y + z = ?" in the work space so that I remember what I'm solving for.
You can bet that in many answer choices, the ACT will have trap answers for other things you can solve for, like x. (This one happens not to, but it's very common).
Strategy 7: Memorize All Formulas and Common Math Facts
If you're still struggling to remember math formulas to solve questions, you haven't gotten to understand ACT Math well enough yet.
Not only does this cost you time, it also indicates that you haven't practiced enough with ACT Math to have the required formulas come to you fluidly.
Memorize the formulas at the front of the section and these common math facts:
- Calculating slope from two points (rise over run)
- Common right triangles: by angles: 45-45-90 (1-1-√2), 30-60-90 (1-2-√3); and by sides: 3-4-5, 5-12-13
- Formulas for arithmetic and geometric sequences
- Formula for diagonal of a rectangular prism
This list isn't complete, but if you study according to my advice above, you'll notice which formulas come up over and over again. You should memorize these.

Strategy 8: Keep a Calm Mind During the Test, No Matter What
Now you know what it takes to achieve perfection on ACT Math.
You know that it's critical to get a perfect raw score, or you might score a 35.
This makes a lot of students freak out during the test.
"I can't solve this question...my 36 is gone...I'm getting more nervous and I have to skip the next question too..."
You can see how quickly you can unravel like this. Before you know it, you're scoring way worse than you ever did on a practice test.
You need to learn to be mentally strong, like an athlete on game day.
Yes, you might have to skip a question on the first pass through. Maybe even two in a row.
But you've practiced hard up to this point. You know this stuff, and you'll come back to those questions and get it later.
You need to keep up a positive mindset during the test, or you'll crumble.
And in the worst case, maybe you won't get a 36. But if you've consistently been getting 36's on the practice tests, you likely won't go much lower than 34—and that's still really good.
In Overview
Those are the main strategies I have for you to improve your ACT math score to a 36. If you're scoring above a 26 right now, with hard work and smart studying, you can raise it to a perfect ACT Math score.
Notice that I didn't actually teach you that much math content. I didn't point to any specific math solutions that will instantly raise your score.
That's because these one-size-fits-all, guaranteed strategies don't really exist. (And anyone who tells you this is deceiving you). Every student is different.
Instead, you need to understand where you're falling short, and drill those weaknesses continuously. You also need to be thoughtful about your mistakes and leave no mistake ignored.
Keep reading for more resources on how to boost your ACT score.
What's Next?
We have a lot more useful guides to raise your ACT score.
Read our complete guide to a perfect 36, written by me, a perfect scorer.
Learn how to write a perfect-scoring 12 ACT essay, step by step.
I built the PrepScholar program based on the principles in this article—the principles that worked for me and thousands of our students.












