Want to test yourself against the most difficult SAT math questions? Want to know what makes these questions so difficult and how best to solve them? If you're ready to really sink your teeth into the SAT math section and have your sights set on that perfect score, then this is the guide for you.
We've put together what we believe to be the 15 most difficult questions for the current Digital SAT, with strategies and answer explanations for each. These are all hard SAT Math questions from College Board SAT practice tests, which means understanding them is one of the best ways to study for those of you aiming for perfection.
Image: Sonia Sevilla/Wikimedia
Brief Overview of SAT Math
There are two sections on the SAT: SAT Reading and Writing and SAT Math. Both sections are divided into two modules, and SAT Reading and Writing always comes first. So, the SAT Math modules will be the 3rd and 4th modules you’ll see on test day. Both math modules allow you to use a calculator.
Each math module is arranged in order of ascending difficulty (where the longer it takes to solve a problem and the fewer people who answer it correctly, the more difficult it is). On each module, question 1 will be "easy" and question 22 will be considered "difficult." The modules are made up of both multiple choice and grid-in questions, and there isn’t a particular order for grid-ins—they can come anywhere in the module and be of any difficulty. 75% of SAT Math questions are multiple choice and 25% are grid-ins.
With very few exceptions, then, the most difficult SAT math problems will be clustered at the end of each module. In addition to their placement on the test, though, these questions also share a few other commonalities. In a minute, we'll look at example questions and how to solve them, then analyze them to figure out what these types of questions have in common.
But First: Should You Be Focusing on the Hardest Math Questions Right Now?
If you're just getting started in your study prep (or if you've simply skipped this first, crucial step), definitely stop and take a full practice test to gauge your current scoring level. Check out our guide to all the free SAT practice tests available online and then sit down to take a test all at once.
The absolute best way to assess your current level is to simply take the SAT practice test as if it were real, keeping strict timing and working straight through with only the allowed breaks (we know—probably not your favorite way to spend a Saturday). Once you've got a good idea of your current level and percentile ranking, you can set milestones and goals for your ultimate SAT Math score.
If you're currently scoring in the 200-400 or the 400-600 range on SAT Math, your best bet is first to check out our guide to improving your math score to be consistently at or over a 600 before you start in trying to tackle the most difficult math problems on the test.
If, however, you're already scoring above a 600 on the Math section and want to test your mettle for the real SAT, then definitely proceed to the rest of this guide. If you're aiming for perfect (or close to), then you'll need to know what the most difficult SAT math questions look like and how to solve them. And luckily, that's exactly what we'll do.
There are a limited number of official SAT practice tests, especially now that the SAT has gone completely digital. We recommend beginning with the six official, digital SAT practice tests available through College Board’s Bluebook software. If you’ve finished those and want even more prep, though, there are lots of older (but still officially produced by the College Board) tests you can use. Most of the questions below are from these practice tests, so if you’re worried about spoiling those tests, stop reading this guide now and come back when you’ve completed all the older official practice tests.

Now let's get to our list of questions (whoo)!
Image: Niytx/DeviantArt
The 15 Hardest SAT Math Questions
Now that you're sure you should be attempting these questions, let's dive right in! We've curated 15 of the most difficult SAT Math questions for you to try below, along with walkthroughs of how to get the answer (if you're stumped).
Question 1
$$C=5/9(F-32)$$
The equation above shows how temperature $F$, measured in degrees Fahrenheit, relates to a temperature $C$, measured in degrees Celsius. Based on the equation, which of the following must be true?
- A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of $5/9$ degree Celsius.
- A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
- A temperature increase of $5/9$ degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.
A) I only
B) II only
C) III only
D) I and II only
ANSWER EXPLANATION: Think of the equation as an equation for a line
$$y=mx+b$$
where in this case
$$C= {5}/{9} (F−32)$$
or
$$C={5}/{9}F −{5}/{9}(32)$$
You can see the slope of the graph is ${5}/{9}$, which means that for an increase of 1 degree Fahrenheit, the increase is ${5}/{9}$ of 1 degree Celsius.
$$C= {5}/{9} (F)$$
$$C= {5}/{9} (1)= {5}/{9}$$
Therefore, statement I is true. This is the equivalent to saying that an increase of 1 degree Celsius is equal to an increase of ${9}/{5}$ degrees Fahrenheit.
$$C= {5}/{9} (F)$$
$$1= {5}/{9} (F)$$
$$(F)={9}/{5}$$
Since ${9}/{5}$ = 1.8, statement II is true.
The only answer that has both statement I and statement II as true is D, but if you have time and want to be absolutely thorough, you can also check to see if statement III (an increase of ${5}/{9}$ degree Fahrenheit is equal to a temperature increase of 1 degree Celsius) is true:
$$C= {5}/{9} (F)$$
$$C= {5}/{9} ({5}/{9})$$
$$C= {25} /{81} (\which \is ≠ 1)$$
An increase of $5/9$ degree Fahrenheit leads to an increase of ${25}/{81}$, not 1 degree, Celsius, and so Statement III is not true.
The final answer is D.
Question 2
The equation ${24x^2 + 25x -47}/{ax-2} = -8x-3-{53/{ax-2}}$ is true for all values of $x≠2/a$, where $a$ is a constant.
What is the value of $a$?
A) -16
B) -3
C) 3
D) 16
ANSWER EXPLANATION: There are two ways to solve this question. The faster way is to multiply each side of the given equation by $ax-2$ (so you can get rid of the fraction). When you multiply each side by $ax-2$, you should have:
$$24x^2 + 25x - 47 = (-8x-3)(ax-2) - 53$$
You should then multiply $(-8x-3)$ and $(ax-2)$ using FOIL.
$$24x^2 + 25x - 47 = -8ax^2 - 3ax +16x + 6 - 53$$
Then, reduce on the right side of the equation
$$24x^2 + 25x - 47 = -8ax^2 - 3ax +16x - 47$$
Since the coefficients of the $x^2$-term have to be equal on both sides of the equation, $−8a = 24$, or $a = −3$.
The other option which is longer and more tedious is to attempt to plug in all of the answer choices for a and see which answer choice makes both sides of the equation equal. Again, this is the longer option, and I do not recommend it for the actual SAT as it will waste too much time.
The final answer is B.
Question 3
If $3x-y = 12$, what is the value of ${8^x}/{2^y}$?
A) $2^{12}$
B) $4^4$
C) $8^2$
D) The value cannot be determined from the information given.
ANSWER EXPLANATION: One approach is to express
$${8^x}/{2^y}$$
so that the numerator and denominator are expressed with the same base. Since 2 and 8 are both powers of 2, substituting $2^3$ for 8 in the numerator of ${8^x}/{2^y}$ gives
$${(2^3)^x}/{2^y}$$
which can be rewritten
$${2^3x}/{2^y}$$
Since the numerator and denominator of have a common base, this expression can be rewritten as $2^(3x−y)$. In the question, it states that $3x − y = 12$, so one can substitute 12 for the exponent, $3x − y$, which means that
$${8^x}/{2^y}= 2^12$$
The final answer is A.
Question 4
Points A and B lie on a circle with radius 1, and arc ${AB}↖⌢$ has a length of $π/3$. What fraction of the circumference of the circle is the length of arc ${AB}↖⌢$?
ANSWER EXPLANATION: To figure out the answer to this question, you'll first need to know the formula for finding the circumference of a circle.
The circumference, $C$, of a circle is $C = 2πr$, where $r$ is the radius of the circle. For the given circle with a radius of 1, the circumference is $C = 2(π)(1)$, or $C = 2π$.
To find what fraction of the circumference the length of ${AB}↖⌢$ is, divide the length of the arc by the circumference, which gives $π/3 ÷ 2π$. This division can be represented by $π/3 * {1/2}π = 1/6$.
The fraction $1/6$ can also be rewritten as $0.166$ or $0.167$.
The final answer is $1/6$, $0.166$, or $0.167$.
Question 5
$${8-i}/{3-2i}$$
If the expression above is rewritten in the form $a+bi$, where $a$ and $b$ are real numbers, what is the value of $a$? (Note: $i=√{-1}$)
ANSWER EXPLANATION: To rewrite ${8-i}/{3-2i}$ in the standard form $a + bi$, you need to multiply the numerator and denominator of ${8-i}/{3-2i}$ by the conjugate, $3 + 2i$. This equals
$$({8-i}/{3-2i})({3+2i}/{3+2i})={24+16i-3+(-i)(2i)}/{(3^2)-(2i)^2}$$
Since $i^2=-1$, this last fraction can be reduced simplified to
$$ {24+16i-3i+2}/{9-(-4)}={26+13i}/{13}$$
which simplifies further to $2 + i$. Therefore, when ${8-i}/{3-2i}$ is rewritten in the standard form a + bi, the value of a is 2.
The final answer is A.
Question 6
In triangle $ABC$, the measure of $∠B$ is 90°, $BC=16$, and $AC$=20. Triangle $DEF$ is similar to triangle $ABC$, where vertices $D$, $E$, and $F$ correspond to vertices $A$, $B$, and $C$, respectively, and each side of triangle $DEF$ is $1/3$ the length of the corresponding side of triangle $ABC$. What is the value of $sinF$?
ANSWER EXPLANATION: Triangle ABC is a right triangle with its right angle at B. Therefore, $\ov {AC}$ is the hypotenuse of right triangle ABC, and $\ov {AB}$ and $\ov {BC}$ are the legs of right triangle ABC. According to the Pythagorean theorem,
$$AB =√{20^2-16^2}=√{400-256}=√{144}=12$$
Since triangle DEF is similar to triangle ABC, with vertex F corresponding to vertex C, the measure of $\angle ∠ {F}$ equals the measure of $\angle ∠ {C}$. Therefore, $sin F = sin C$. From the side lengths of triangle ABC,
$$sinF ={\opposite \side}/{\hypotenuse}={AB}/{AC}={12}/{20}={3}/{5}$$
Therefore, $sinF ={3}/{5}$.
The final answer is ${3}/{5}$ or 0.6.
Question 7
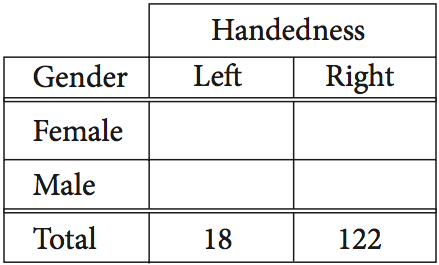
The incomplete table above summarizes the number of left-handed students and right-handed students by gender for the eighth grade students at Keisel Middle School. There are 5 times as many right-handed female students as there are left-handed female students, and there are 9 times as many right-handed male students as there are left-handed male students. if there is a total of 18 left-handed students and 122 right-handed students in the school, which of the following is closest to the probability that a right-handed student selected at random is female? (Note: Assume that none of the eighth-grade students are both right-handed and left-handed.)
A) 0.410
B) 0.357
C) 0.333
D) 0.250
ANSWER EXPLANATION: In order to solve this problem, you should create two equations using two variables ($x$ and $y$) and the information you're given. Let $x$ be the number of left-handed female students and let $y$ be the number of left-handed male students. Using the information given in the problem, the number of right-handed female students will be $5x$ and the number of right-handed male students will be $9y$. Since the total number of left-handed students is 18 and the total number of right-handed students is 122, the system of equations below must be true:
$$x + y = 18$$
$$5x + 9y = 122$$
When you solve this system of equations, you get $x = 10$ and $y = 8$. Thus, 5*10, or 50, of the 122 right-handed students are female. Therefore, the probability that a right-handed student selected at random is female is ${50}/{122}$, which to the nearest thousandth is 0.410.
The final answer is A.
Questions 8 & 9
Use the following information for both question 7 and question 8.
If shoppers enter a store at an average rate of $r$ shoppers per minute and each stays in the store for average time of $T$ minutes, the average number of shoppers in the store, $N$, at any one time is given by the formula $N=rT$. This relationship is known as Little's law.
The owner of the Good Deals Store estimates that during business hours, an average of 3 shoppers per minute enter the store and that each of them stays an average of 15 minutes. The store owner uses Little's law to estimate that there are 45 shoppers in the store at any time.
Question 8
Little's law can be applied to any part of the store, such as a particular department or the checkout lines. The store owner determines that, during business hours, approximately 84 shoppers per hour make a purchase and each of these shoppers spend an average of 5 minutes in the checkout line. At any time during business hours, about how many shoppers, on average, are waiting in the checkout line to make a purchase at the Good Deals Store?
ANSWER EXPLANATION: Since the question states that Little's law can be applied to any single part of the store (for example, just the checkout line), then the average number of shoppers, $N$, in the checkout line at any time is $N = rT$, where $r$ is the number of shoppers entering the checkout line per minute and $T$ is the average number of minutes each shopper spends in the checkout line.
Since 84 shoppers per hour make a purchase, 84 shoppers per hour enter the checkout line. However, this needs to be converted to the number of shoppers per minute (in order to be used with $T = 5$). Since there are 60 minutes in one hour, the rate is ${84 \shoppers \per \hour}/{60 \minutes} = 1.4$ shoppers per minute. Using the given formula with $r = 1.4$ and $T = 5$ yields
$$N = rt = (1.4)(5) = 7$$
Therefore, the average number of shoppers, $N$, in the checkout line at any time during business hours is 7.
The final answer is 7.
Question 9
The owner of the Good Deals Store opens a new store across town. For the new store, the owner estimates that, during business hours, an average of 90 shoppers per hour enter the store and each of them stays an average of 12 minutes. The average number of shoppers in the new store at any time is what percent less than the average number of shoppers in the original store at any time? (Note: Ignore the percent symbol when entering your answer. For example, if the answer is 42.1%, enter 42.1)
ANSWER EXPLANATION: According to the original information given, the estimated average number of shoppers in the original store at any time (N) is 45. In the question, it states that, in the new store, the manager estimates that an average of 90 shoppers per hour (60 minutes) enter the store, which is equivalent to 1.5 shoppers per minute (r). The manager also estimates that each shopper stays in the store for an average of 12 minutes (T). Thus, by Little's law, there are, on average, $N = rT = (1.5)(12) = 18$ shoppers in the new store at any time. This is
$${45-18}/{45} * 100 = 60$$
percent less than the average number of shoppers in the original store at any time.
The final answer is 60.
Question 10
In the $xy$-plane, the point $(p,r)$ lies on the line with equation $y=x+b$, where $b$ is a constant. The point with coordinates $(2p, 5r)$ lies on the line with equation $y=2x+b$. If $p≠0$, what is the value of $r/p$?
A) $2/5$
B) $3/4$
C) $4/3$
D) $5/2$
ANSWER EXPLANATION: Since the point $(p,r)$ lies on the line with equation $y=x+b$, the point must satisfy the equation. Substituting $p$ for $x$ and $r$ for $y$ in the equation $y=x+b$ gives $r=p+b$, or $\bi b$ = $\bi r-\bi p$.
Similarly, since the point $(2p,5r)$ lies on the line with the equation $y=2x+b$, the point must satisfy the equation. Substituting $2p$ for $x$ and $5r$ for $y$ in the equation $y=2x+b$ gives:
$5r=2(2p)+b$
$5r=4p+b$
$\bi b$ = $\bo 5 \bi r-\bo 4\bi p$.
Next, we can set the two equations equal to $b$ equal to each other and simplify:
$b=r-p=5r-4p$
$3p=4r$
Finally, to find $r/p$, we need to divide both sides of the equation by $p$ and by $4$:
$3p=4r$
$3={4r}/p$
$3/4=r/p$
The correct answer is B, $3/4$.
If you picked choices A and D, you may have incorrectly formed your answer out of the coefficients in the point $(2p, 5r)$. If you picked Choice C, you may have confused $r$ and $p$.
Note that while this is in the calculator section of the SAT, you absolutely do not need your calculator to solve it!
Question 11
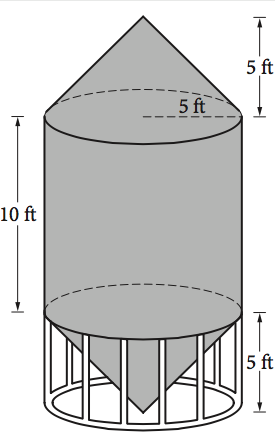 A grain silo is built from two right circular cones and a right circular cylinder with internal measurements represented by the figure above. Of the following, which is closest to the volume of the grain silo, in cubic feet?
A grain silo is built from two right circular cones and a right circular cylinder with internal measurements represented by the figure above. Of the following, which is closest to the volume of the grain silo, in cubic feet?
A) 261.8
B) 785.4
C) 916.3
D) 1047.2
ANSWER EXPLANATION: The volume of the grain silo can be found by adding the volumes of all the solids of which it is composed (a cylinder and two cones). The silo is made up of a cylinder (with height 10 feet and base radius 5 feet) and two cones (each with height 5 ft and base radius 5 ft). The formulas given at the beginning of the SAT Math section:
Volume of a Cone
$$V={1}/{3}πr^2h$$
Volume of a Cylinder
$$V=πr^2h$$
can be used to determine the total volume of the silo. Since the two cones have identical dimensions, the total volume, in cubic feet, of the silo is given by
$$V_{silo}=π(5^2)(10)+(2)({1}/{3})π(5^2)(5)=({4}/{3})(250)π$$
which is approximately equal to 1,047.2 cubic feet.
The final answer is D.
Question 12
If $x$ is the average (arithmetic mean) of $m$ and $9$, $y$ is the average of $2m$ and $15$, and $z$ is the average of $3m$ and $18$, what is the average of $x$, $y$, and $z$ in terms of $m$?
A) $m+6$
B) $m+7$
C) $2m+14$
D) $3m + 21$
ANSWER EXPLANATION: Since the average (arithmetic mean) of two numbers is equal to the sum of the two numbers divided by 2, the equations $x={m+9}/{2}$, $y={2m+15}/{2}$, $z={3m+18}/{2}$are true. The average of $x$, $y$, and $z$ is given by ${x + y + z}/{3}$. Substituting the expressions in m for each variable ($x$, $y$, $z$) gives
$$[{m+9}/{2}+{2m+15}/{2}+{3m+18}/{2}]/3$$
This fraction can be simplified to $m + 7$.
The final answer is B.
Question 13
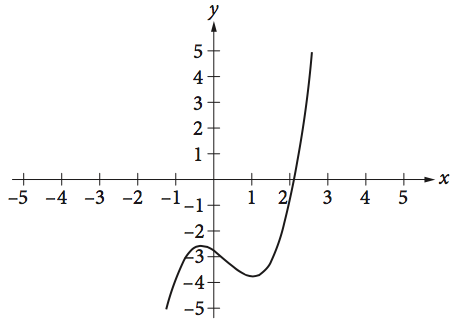
The function $f(x)=x^3-x^2-x-{11/4}$ is graphed in the $xy$-plane above. If $k$ is a constant such that the equation $f(x)=k$ has three real solutions, which of the following could be the value of $k$?
ANSWER EXPLANATION: The equation $f(x) = k$ gives the solutions to the system of equations
$$y = f(x) = x^3-x^2-x-{11}/{4}$$
and
$$y = k$$
A real solution of a system of two equations corresponds to a point of intersection of the graphs of the two equations in the $xy$-plane.
The graph of $y = k$ is a horizontal line that contains the point $(0, k)$ and intersects the graph of the cubic equation three times (since it has three real solutions). Given the graph, the only horizontal line that would intersect the cubic equation three times is the line with the equation $y = −3$, or $f(x) = −3$. Therefore, $k$ is $-3$.
The final answer is D.
Question 14
$$q={1/2}nv^2$$
The dynamic pressure $q$ generated by a fluid moving with velocity $v$ can be found using the formula above, where $n$ is the constant density of the fluid. An aeronautical engineer users the formula to find the dynamic pressure of a fluid moving with velocity $v$ and the same fluid moving with velocity 1.5$v$. What is the ratio of the dynamic pressure of the faster fluid to the dynamic pressure of the slower fluid?
ANSWER EXPLANATION: To solve this problem, you need to set up to equations with variables. Let $q_1$ be the dynamic pressure of the slower fluid moving with velocity $v_1$, and let $q_2$ be the dynamic pressure of the faster fluid moving with velocity $v_2$. Then
$$v_2 =1.5v_1$$
Given the equation $q = {1}/{2}nv^2$, substituting the dynamic pressure and velocity of the faster fluid gives $q_2 = {1}/{2}n(v_2)^2$. Since $v_2 =1.5v_1$, the expression $1.5v_1$ can be substituted for $v_2$ in this equation, giving $q_2 = {1}/{2}n(1.5v_1)^2$. By squaring $1.5$, you can rewrite the previous equation as
$$q_2 = (2.25)({1}/{2})n(v_1)^2 = (2.25)q_1$$
Therefore, the ratio of the dynamic pressure of the faster fluid is
$${q2}/{q1} = {2.25 q_1}/{q_1}= 2.25$$
The final answer is 2.25 or 9/4.
Question 15
For a polynomial $p(x)$, the value of $p(3)$ is $-2$. Which of the following must be true about $p(x)$?
A) $x-5$ is a factor of $p(x)$.
B) $x-2$ is a factor of $p(x)$.
C) $x+2$ is a factor of $p(x)$.
D) The remainder when $p(x)$ is divided by $x-3$ is $-2$.
ANSWER EXPLANATION: If the polynomial $p(x)$ is divided by a polynomial of the form $x+k$ (which accounts for all of the possible answer choices in this question), the result can be written as
$${p(x)}/{x+k}=q(x)+{r}/{x+k}$$
where $q(x)$ is a polynomial and $r$ is the remainder. Since $x + k$ is a degree-1 polynomial (meaning it only includes $x^1$ and no higher exponents), the remainder is a real number.
Therefore, $p(x)$ can be rewritten as $p(x) = (x + k)q(x) + r$, where $r$ is a real number.
The question states that $p(3) = -2$, so it must be true that
$$-2 = p(3) = (3 + k)q(3) + r$$
Now we can plug in all the possible answers. If the answer is A, B, or C, $r$ will be $0$, while if the answer is D, $r$ will be $-2$.
A. $-2 = p(3) = (3 + (-5))q(3) + 0$
$-2=(3-5)q(3)$
$-2=(-2)q(3)$
This could be true, but only if $q(3)=1$
B. $-2 = p(3) = (3 + (-2))q(3) + 0$
$-2 = (3-2)q(3)$
$-2 = (-1)q(3)$
This could be true, but only if $q(3)=2$
C. $-2 = p(3) = (3 + 2)q(3) + 0$
$-2 = (5)q(3)$
This could be true, but only if $q(3)={-2}/{5}$
D. $-2 = p(3) = (3 + (-3))q(3) + (-2)$
$-2 = (3 - 3)q(3) + (-2)$
$-2 = (0)q(3) + (-2)$
This will always be true no matter what $q(3)$ is.
Of the answer choices, the only one that must be true about $p(x)$ is D, that the remainder when $p(x)$ is divided by $x-3$ is -2.
The final answer is D.

You deserve all the naps after running through those questions.
What Do the Hardest SAT Math Questions Have in Common?
It's important to understand what makes these hard questions "hard." By doing so, you'll be able to both understand and solve similar questions when you see them on test day, as well as have a better strategy for identifying and correcting your previous SAT math errors.
In this section, we'll look at what these questions have in common and give examples of each type. Some of the reasons why the hardest math questions are the hardest math questions is because they:
#1: Test Several Mathematical Concepts at Once

Here, we must deal with imaginary numbers and fractions all at once.
Secret to success: Think of what applicable math you could use to solve the problem, do one step at a time, and try each technique until you find one that works!
#2: Involve a Lot of Steps
Remember: the more steps you need to take, the easier to mess up somewhere along the line!

We must solve this problem in steps (doing several averages) to unlock the rest of the answers in a domino effect. This can get confusing, especially if you're stressed or running out of time.
Secret to success: Take it slow, take it step by step, and double-check your work so you don't make mistakes!
#3: Test Concepts That You Have Limited Familiarity With
For example, many students are less familiar with functions than they are with fractions and percentages, so most function questions are considered "high difficulty" problems.

If you don't know your way around functions, this would be a tricky problem.
Secret to success: Review math concepts that you don't have as much familiarity with such as functions. We suggest using our great free SAT Math review guides.
#4: Are Worded in Unusual or Convoluted Ways
It can be difficult to figure out exactly what some questions are asking, much less figure out how to solve them. This is especially true when the question is located at the end of the section, and you are running out of time.

Because this question provides so much information without a diagram, it can be difficult to puzzle through in the limited time allowed.
Secret to success: Take your time, analyze what is being asked of you, and draw a diagram if it's helpful to you.
#5: Use Many Different Variables

With so many different variables in play, it is quite easy to get confused.
Secret to success: Take your time, analyze what is being asked of you, and consider if plugging in numbers is a good strategy to solve the problem (it wouldn't be for the question above, but would be for many other SAT variable questions).
The Take-Aways
The SAT is a marathon and the better prepared you are for it, the better you'll feel on test day. Knowing how to handle the hardest questions the test can throw at you will make taking the real SAT seem a lot less daunting.
If you felt that these questions were easy, make sure not underestimate the effect of adrenaline and fatigue on your ability to solve problems. As you continue to study, always adhere to the proper timing guidelines and try to take full tests whenever possible. This is the best way to recreate the actual testing environment so that you can prepare for the real deal.
If you felt these questions were challenging, be sure to strengthen your math knowledge by checking out our individual math topic guides for the SAT. There, you'll see more detailed explanations of the topics in question as well as more detailed answer breakdowns.
What's Next?
Felt that these questions were harder than you were expecting? Take a look at all the topics covered in the SAT math section and then note which sections were particular difficulty for you. Next, take a gander at our individual math guides to help you shore up any of those weak areas.
Running out of time on the SAT math section? Our guide will help you beat the clock and maximize your score.
Aiming for a perfect score? Check out our guide on how to get a perfect 800 on the SAT math section, written by a perfect-scorer.