
What are the factors of 45? 1, 3, 5, 9, 15, and 45.
Wondering how I came up with those numbers? Factoring! Because it provides a mathematical foundation for more complicated systems, learning how to factor is key. So whether you're studying for an algebra test, brushing up for the SAT or ACT, or just want to refresh and remember how to factor numbers for higher orders of math, this is the guide for you.
What Is Factoring?
Factoring is the process of finding every whole number that can be multiplied by another whole number to equal a target number. Both multiples will be factors of the target number.
Factoring numbers may just seem like a tedious task or rote memorization with no end goal, but factoring is a technique that helps to build the backbone of much more complex mathematical processes.
Without knowing how to factor, it would be downright difficult (if not impossible) to make sense of polynomials and calculus, and would even make simple tasks like divvying up a check that much trickier to figure out in one's head.
What Are the Factors of 45? Factoring in Action
This concept may be difficult to visualize, so let's take a look at all factors of 45 to see this process in action. The factors of 45 are the pairs of numbers that equal 45 when multiplied together:
1 & 45 (because 1 * 45 = 45)
3 & 15 (because 3 * 15 = 45)
5 & 9 (because 5 * 9 = 45)
So in list form, the 45 factors are 1, 3, 5, 9, 15, and 45.
 Luckily for us, factoring only requires the top two functions in this image (yay!)
Luckily for us, factoring only requires the top two functions in this image (yay!)
Prime Factorization and the Prime Factors of 45
A prime number is any whole number greater than 1 that can only be divided (evenly) by 1 and itself. A list of the smallest prime numbers are 2, 3, 5, 7, 11, 13, 17, 19 ... and so on.
Prime factorization means to find the prime number factors of a target number that, when multiplied together, equal that target number. So if we're using 45 as our target number, we want to find only the prime factors of 45 which need to be multiplied together to equal 45.
We know from the factors of 45 list above that only some of those factors (3 and 5) are prime numbers. But we also know that 3 * 5 does not equal 45. So 3 * 5 is an incomplete prime factorization.
The easiest way to find a complete prime factorization of any given target number is to use what is essentially "upside-down" division and dividing only by the smallest prime that can fit into each result.
For example:
Divide the target number (45) by the smallest prime that can factor into it. In this case, it's 3.

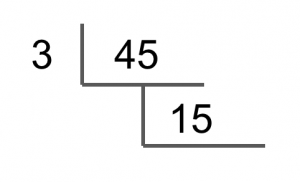
We end up with 15. Now divide 15 by the smallest prime that can factor into it. In this case, it's again 3.
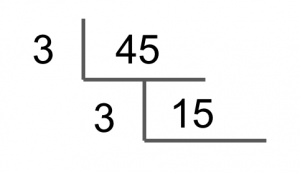
We end up with a result of 5. Now divide 5 by the smallest prime number that can factor into it. In this case, it's 5.
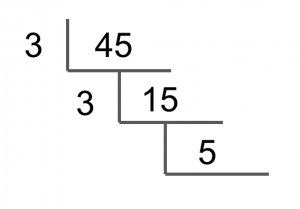
This leaves us with 1, so we're finished.
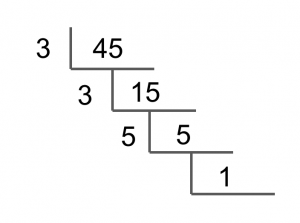
The prime factorization will be all the number on the "outside" multiplied together. When multiplied together, the result will be 45. (Note: we do not include the 1, because 1 is not a prime number.)
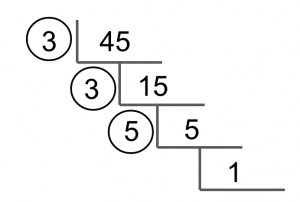
Our final prime factorization of 45 is 3 * 3 * 5.

A different kind of Prime.
Figuring Out the Factors of Any Number
When figuring out factors, the fastest way is to find factor pairs as we did earlier for all the factors of 45. By finding the pairs, you cut your work in half, since you're finding both the smallest and largest factors at the same time.
Now, the fastest way to figure out all the factor pairs you'll need to factor the target number is to find the spare root of the target number (or square root and round down to the closest whole number) and use that number as your stopping point for finding small factors.
Why? Because you'll have already found all the factors larger than the square by finding the factor pairs of smaller factors. And you'll only repeat those factors if you continue to try to find factors larger than the square root.
Don't worry if this sounds confusing right now! We'll work through with an example to show you how you can avoid wasting time finding the same factors again.
So let's see the method in action to find all the factors of 64:
First, let's take the square root of 64.
√64 = 8
Now we know only to focus on whole numbers 1 - 8 to find the first half of all our factor pairs.
#1: Our first factor pair will be 1 & 64
#2: 64 is an even number, so our next factor pair will be 2 & 32.
#3: 64 cannot be evenly divided by 3, so 3 is NOT a factor.
#4: 64/4 = 16, so our next factor pair will be 4 & 16.
#5: 64 is not evenly divisible by 5, so 5 is NOT a factor of 64.
#6: 6 does not go evenly into 64, so 6 is NOT a factor of 64.
#7: 7 does not go evenly in 64, so 7 is NOT a factor of 64.
#8: 8 * 8 (8 squared) is equal to 64, so 8 is a factor of 64.
And we can stop here, because 8 is the square root of 64. If we were to continue trying to find factors, we would only repeat the larger numbers from our earlier factor pairs (16, 32, 64).
Our final list of factors of 64 is 1, 2, 4, 8, 16, 32, and 64.

Factors (like ducklings) are always better in pairs.
Factor-Finding Shortcuts
Now let's see how we can quickly find the smallest factors (and thus the factor pairs) of a target number. Below, I've outlined some helpful tricks to tell if the numbers 1-11 are factors of a given number.
1) Whenever you want to factor a number, you can always start immediately with two factors: 1 and the target number (for example, 1 & 45, if you're factoring 45). Any number (other than 0) can always be multiplied by 1 to equal itself, so 1 will always be a factor.
2) If the target number is even, your next factors will be 2 and half of the target number. If the number is odd, you automatically know it can't be divided evenly by 2, and so 2 will NOT be a factor. (In fact, if the target number is odd, it won't have factors of ANY even number.)
3) A quick way to figure out if a number is divisible by 3 is to add up the digits in the target number. If 3 is a factor of the digit sum, then 3 is a factor of the target number as well.
For example, say our target number is 117 and we must factor it. We can figure out if 3 is a factor by adding the digits of the target number (117) together:
1 + 1 + 7 = 9
3 can be multiplied by 3 to equal 9, so 3 will be able to go evenly into 117.
117/3 = 39
3 & 39 are factors of 117.
4) A target number will only have a factor of 4 if that target number is even. If it is, you can figure out if 4 is a factor by looking at the result of an earlier factor pair. If, when dividing a target number by 2, the result is still even, the target number will also be divisible by 4. If not, the target number will NOT have a factor of 4.
For example:
18/2 = 9. 18 is NOT divisible by 4 because 9 is an odd number.
56/2 = 28. 56 IS divisible by 4 because 28 is an even number.
5) 5 will be a factor of any and all numbers ending in the digits 5 or 0. If the target ends in any other number, it will not have a factor of 5.
6) 6 will always be a factor of a target number if the target number has factors of BOTH 2 and 3. If not, 6 will not be a factor.
7) Unfortunately, there aren't any shortcuts to find if 7 is a factor of a number other than remembering the multiples of 7.
8) If the target number does NOT have factors of 2 and 4, it won't have a factor of 8 either. If it does have factors of 2 and 4, it might have a factor of 8, but you'll have to divide to see (unfortunately, there's no neat trick for it beyond that and remembering the multiples of 8).
9) You can figure out if 9 is a factor by adding the digits of the target number together. If they add up to a multiple of 9 then the target number does have 9 as factor.
For example:
42 → 4 + 2 = 6. 6 is NOT divisible by 9, so 9 is NOT a factor of 42.
72→ 7 + 2 = 9. 9 IS divisible by 9 (obviously!), so 9 is a factor of 72.
10) If a target number ends in 0, then it will always have a factor of 10. If not, 10 won't be a factor.
11) If a target number is a two digit number with both digits repeating (22, 33, 66, 77…), then it will have 11 as a factor. If it is a three digit number or higher, you'll have to simply test out whether its divisible by 11 yourself.
12+) At this point, you've probably already found your larger numbers like 12 and 13 and 14 by finding your smaller factors and making factor pairs. If not, you'll have to test them out manually by dividing them into your target number.

Learning your quick-factoring techniques will allow all those pesky pieces to fall right into place.
Tips for Remembering 45 Factors
If your goal is to remember all factors of 45, then you can always use the above techniques for finding factor pairs.
The square root of 45 is somewhere between 6 and 7 (6^2 = 36 and 7^2 = 49). Round down to 6, which will be the largest small number you need to test.
You know that the first pair will automatically be 1 & 45. You also know that 2, 4, and 6 won't be factors, because 45 is an odd number.
4 + 5 = 9, so 3 will be a factor (as will 15, because 45/3 = 15).
And finally, 45 ends in a 5, so 5 will be a factor (as will 9, because 45/5 = 9).
This goes to show that you can always figure out the factors of 45 extremely quickly, even if you haven't memorized the exact numbers in the list.
Or, if you'd rather memorize all 45 factors specifically, you could remember that, to factor 45, all you need is the smallest three odd numbers (1, 3, 5). Now just pair them up with their corresponding multiples to get 45 (45, 15, 9).
Conclusion: Why Factoring Matters
Factoring provides the foundation of higher forms of mathematical thought, so learning how to factor will serve you well in both your current and future mathematical endeavors.
Whether you're learning for the first time or just taking the time to refresh your factor knowledge, taking the steps to understand these processes (and knowing the tricks for how to get your factors most efficiently!) will help get you where you want to be in your mathematical life.
Happy Factoring!










