Geometry is the branch of mathematics that deals with points, lines, shapes, and angles. ACT geometry questions will test your knowledge of the shapes, sizes, and volumes of different figures, as well as their positions in space. 33% of ACT math problems (about 18 questions total) will involve geometry, depending on the particular test.
Because geometry as a whole covers so many different mathematical concepts, there are several different subsections of geometry (including planar, solid, and coordinate). We will cover each branch of geometry in separate guides, complete with a step-by-step approach to questions and sample problems.
This article will be your comprehensive guide to solid geometry on the ACT. We’ll take you through the meaning of solid geometry, the formulas and understandings you’ll need to know, and how to tackle some of the most difficult solid geometry questions on the ACT math section.
Before you continue, keep in mind that there will usually only be 1-2 solid geometry questions on any given ACT, so you should prioritize studying planar (flat) geometry and coordinate geometry first. Save learning this guide for last in terms of your ACT geometry math prep.
Before you descend into the realm of solid geometry, make sure you are well versed in plane geometry and coordinate geometry!
What is Solid Geometry?
Solid geometry is the name for geometry performed in three dimensions. Another dimension--volume--is added to planar (flat) geometry, which only uses height and length.
Instead of flat shapes like circles, squares, and triangles, solid geometry deals with spheres, cubes, and pyramids (along with any other three-dimensional shapes). And instead of using perimeter and area to measure flat shapes, solid geometry uses surface area and volume to measure its three-dimensional shapes.
A circle is a flat object. This is plane geometry.
A sphere is a three-dimensional object. This is solid geometry.
On the ACT, most of the solid geometry problems are located at the end of the math section. This means solid geometry problems are considered some of the most challenging questions on ACT math (or ones that will take the longest amount of time, as they often need to be completed in multiple pieces). Use this knowledge to direct your study-focus to the most productive avenues.
If you are getting several questions wrong on the first 40 questions in the math section, it might be more productive for you to take the time to first refresh your overall understanding of the math concepts covered by the ACT. You may also want to look over all the ACT math formulas you’ll need.
Note: some of these formulas are given to you on the test in the question itself, but this is often inconsistent. For example, on some ACTs, the formula for the volume of a cylinder is given, other times it is not. If you're unsure which formulas are given or not given in the math section, refresh your formulas knowledge.
Though many of the formulas are given, it is still important for you to understand how they work and why. The formulas marked “Necessary to know” are ones you should memorize, but the others will all be given. So don’t worry too much about memorizing them, but do pay attention to them in order to deepen your understanding of the principles behind solid geometry on the ACT.
In this guide, I’ve divided the approach to ACT solid geometry into three categories:
#1: Typical ACT solid geometry questions
#2: Types of geometric solids and their formulas
#3: How to solve an ACT solid geometry problem
Solid geometry adventure here we come!
Typical Solid Geometry Questions on the ACT
Before we go through the formulas you'll need to tackle solid geometry, it's important to familiarize yourself with the kinds of questions the ACT will ask you about solids. ACT solid geometry questions will appear in two formats: questions in which you are given a diagram, and word problem questions.
No matter the format, each type of ACT solid geometry question exists to test your understanding of the volume and/or surface area of a figure. You will be asked how to find the volume or surface area of a figure, or you'll be asked to identify how a shape's dimensions shift and change.
Diagram Problems
A solid geometry diagram problem will provide you with a drawing of a geometrical solid and ask you to find a missing element of the picture. Sometimes they will ask you to find the volume of the figure, the surface area of the figure, or the distance between two points on the figure. They may also ask you to compare the volumes, surface areas, or distances of several different figures.
Word Problems
Solid geometry word problems will usually ask you to compare the surface areas or volumes of two shapes. They will often give you the dimensions of one solid and then tell you to compare its volume or surface area to a solid with different dimensions.
Other word problems might ask you to contain one shape within another. This is just another way of getting you to think about a shape's volume and ways to measure it.
What is the minimum possible volume of a cube, in cubic inches, that could inscribe a sphere with a radius of 3 inches?
A) $12√3$ (approximately $20.78$)
B) $24√3$ (approximately $41.57$)
C) $36√3$ (approximately $62.35$)
D) $216$
E) $1728$
This is a typical inscribing solids word problem. We'll go through how to solve it later in the guide.
Solid geometry word problems can be confusing to many people, because it can be difficult to visualize the question without a picture.
As always with word problems that describe shapes or angles, make the drawing yourself! Simply being able to see what a question is describing can do wonders to help clarify the question.
Overall
Every solid geometry question on the ACT is concerned with either the volume or surface area of a figure, or the distance between two points on a figure. Sometimes you'll have to combine surface area and volume, sometimes you'll have to compare two solids to one another. But, ultimately, all solid geometry questions boil down to these concepts.
So now let's go through our ACT math tips on how to find volumes, surface areas, and distances of all the different geometric solids.
A perfect example of geometric solids in the wild
Prisms
A prism is a three-dimensional shape that has (at least) two congruent, parallel bases. Basically, you could pick up a prism and carry it with its opposite sides lying flat against your palms.
A few of the many different kinds of prisms.
Rectangular Solids
A rectangular solid is essentially a box. It has three pairs of opposite sides that are congruent and parallel.
Volume
Necessary to know
$\Volume = lwh$
The volume of a figure is the measure of its interior space.
- $l$ is the length of the figure
- $w$ is the width of the figure
- $h$ is the height of the figure
Notice how this formula is the same as finding the area of the square ($A = lw$) with the added dimension of height, as this is a three-dimensional figure.
First, identify the type of question--is it asking for volume or surface area? The question asks about the interior space of a solid, so it's a volume question.
Now we need to find a rectangular volume, but this question is somewhat tricky. Notice that we're finding out how much water is in a particular fish tank, but the water does not fill up the entire tank. If we just focus on the water, we would find that it has a volume of:
$V = lwh$ => $(4)(3)(1) = 12\cubic\feet$
(Why did we multiply the feet and width by 1 instead of 2? Because the water only comes up to 1 foot; it does not fill up the entire 2 feet of height of the tank.)
Now we are going to put that 12 cubic feet of water into a second tank. This second tank has a total volume of:
$V = lwh$ => $(3)(2)(4) = 24\cubic\feet$
Although the second tank can hold 24 cubic feet of water, we are only putting in 12. So $12/24 = 1/2$.
The water will come up at exactly half the height of the second tank, which means the answer is D, 2 feet.
Either way, those fish won't be very happy in half a tank of water
Surface Area
Necessary to know
$\Surface\area = 2lw + 2lh + 2wh$
To find the surface area of a rectangular prism, you're finding the areas for all the flat rectangles on the surface of the figure (the faces) and then adding those areas together.
In a rectangular solid, there are six faces on the outside of the figure. They are divided into three congruent pairs of opposite sides.
If you find it difficult to picture surface area, remember that a die has six sides.
So you are finding the areas of the three combinations of length, width, and height ($lw$, $lh$, and $wh$), which you then multiply by two because there are two sides for each of these combinations. The resulting areas are then all added together to get the surface area.
Diagonal Length
Necessary to know
(Note: it will be necessary for you to know how to find the diagonal, but you don't have to memorize the formula. Continue reading for more details on this.)
$\Diagonal = √[l^2 + w^2 + h^2]$
The diagonal of a rectangular solid is the longest interior line of the solid. It touches from the corner of one side of the prism to the opposite corner on the other.
You can find this diagonal by either using the above formula or by breaking up the figure into two flat triangles and using the Pythagorean Theorem for both. You can always do this is you do not want to memorize the formula or if you're afraid of misremembering the formula on test day.
First, find the length of the diagonal (hypotenuse) of the base of the solid using the Pythagorean Theorem.
$c^2 = l^2 + w^2$
Next, use that length as one of the smaller sides of a new triangle with the diagonal of the rectangular solid as the new hypotenuse.
$d^2 = c^2 + h^2$
And solve for the diagonal using the Pythagorean Theorem again.
Cubes
Cubes are a special kind of rectangular solid, just like squares are a special type of rectangle.
A cube has a height, length, and width that are all equal. The six faces on a cube's surface are also all congruent.
Volume
Necessary to know
$\Volume = s^3$
- $s$ is the length of the side of a cube (any side of the cube, as they are all the same).
This is the same thing as finding the volume of a rectangular solid ($v = lwh$), but, because their sides are all equal, you can simplify it by saying $s^3$.
First, identify what the question is asking you to do. You're trying to fit smaller rectangles into a larger rectangle, so you're dealing with volume, not surface area. Find the volume of the larger rectangle (which in this case is a cube).
So you can use the formula for the volume of a cube:
$\Volume = s^3$ => $6^3 = 216$
Or you can use the formula to find the volume of any rectangular solid:
$\Volume = lwh$ => $(6)(6)(6) = 216$
Now find the volume of one of the smaller rectangular solids:
$\Volume = lwh$ => $(3)(2)(1) = 6$
And divide the larger rectangular solid by the smaller to find out how many of the smaller rectangular solids can fit inside the larger:
$216/6 = 36$
So your final answer is D, 36
Surface Area
Necessary to know
$\Surface\area = 6s^2$
This is the same formulas as the surface area for a rectangular solid ($SA = 2lw + 2lh + 2hw$). Because all the sides are the same in a cube, you can see how $6s^2$ was derived:
$2lw + 2lh + 2hw$ => $2ss + 2ss + 2ss$ => $2s^2 + 2s^2 + 2s^2$ => $6s^2$
You can approach this question in two ways: by using the formula or by doing it out longhand.
If you use the formula for the surface area of a cube, you can say:
$\Surface\area = (6)(3^2)$
$SA = (6)(9) = 54$
If you forget the formula (or are afraid of messing it up come test day), you can always do it out longhand:
$\Surface\area = ss + ss + ss + ss + ss + ss$
or $SA = (ss)(6)$
(Remember that there are six faces on a cube like the six faces on a die)
$SA = (3)(3) + (3)(3) + (3)(3) + (3)(3) + (3)(3) + (3)(3)$
or $SA = (3)(3)(6)$
$SA = 9 + 9 + 9 + 9 + 9 + 9 = 9(6) = 54$
Either way, you get the answer K, 54
Diagonal Length
Necessary to know
(Note: it will be necessary for you to know how to find the diagonal, but you don't have to memorize the formula. Continue reading for more details on this.)
$\Diagonal = s√3$
Just as with the rectangular solid, you can break up the cube into two flat triangles and use the Pythagorean Theorem for both as an alternative to the formula.
This is the exact same process as finding the diagonal of a rectangular solid.
First, find the length of the diagonal (hypotenuse) of the base of the solid using the Pythagorean Theorem.
Next, use that length as one of the smaller sides of a new triangle with the diagonal of the rectangular solid as the new hypotenuse.
Solve for the diagonal using the Pythagorean Theorem again.
Cylinders
A cylinder is a prism with two circular bases on its opposite sides
Volume
Necessary to know
$\Volume = πr^2h$
- $π$ is the universal constant, also represented as 3.14(159)
- $r$ is the radius of the circular base. It is any straight line drawn from the center of the circle to the circumference of the circle.
- $h$ is the height of the circle. It is the straight line drawn connecting the two circular bases.
This problem gives you the formula for a cylinder, but the ACT is often inconsistent about this. Notice that this is problem #29 (an easy-medium level question), so you're given the formula. If this had been question #49, you would likely not have been given the formula.
But because you're given the formula, it's easy to plug in your values into it. Pay attention, however, to exactly what the question is asking you to do. Just like with the fish tank question above, you are not being asked to fill up the whole container with water, only some of it.
So if $\volume = πr^2h$, then $V = π(12^2)(5)$
(The radius is 12 because a radius is half the diameter, and the full diameter is 24. The height is 5 because the question tells us that we are only filling up the container to 5 feet).
$V = 720π = 2,261.9448$
So the answer is C, 2,262
Surface Area
$\Surface\area = 2πr^2 +2πrh$
To find the surface area of a cylinder, you're adding the volume of the two circular bases ($2πr^2$), plus the surface of the tube as if it were unrolled ($2πrh$).
The surface of the tube can also be written as $SA = πdh$, because the diameter is twice the radius. In other words, the surface of the tube is the formula for the circumference of a circle with the additional dimension of height.
Non-Prism Solids
Non-prism solids are shapes in three dimensions that do not have any parallel, congruent sides. If you picked these shapes up with your hand, a maximum of one side (if any) would lie flat against your palm.
Cones
A cone is similar to a cylinder, but has only one circular base instead of two. Its opposite end terminates in a point, rather than a circle.
There are two kind of cones--right cones and oblique cones. For the purposes of the ACT, you only have to concern yourself with right cones. Oblique cones will never appear on the ACT.
A right cone has an apex (the terminating point on top) that sits directly above the center of the cone’s circular base.
When a height ($h$) is dropped from the apex to the center of the circle, it makes a right angle with the circular base.
Volume
$\Volume = 1/3πr^2h$
- $π$ is a constant, written as 3.14(159)
- $r$ is the radius of the circular base
- $h$ is the height, drawn at a right angle from the cone’s apex to the center of the circular base
The volume of a cone is $1/3$ the volume of a cylinder. This makes sense logically, as a cone is basically a cylinder with one base collapsed into a point. So a cone’s volume will be less than that of a cylinder.
Surface Area
$\Surface\area = πr^2 + pirl$
- $l$ is the length of the side of the cone extending from the apex to the circumference of the circular base
The surface area is the combination of the area of the circular base ($πr^2$) and the lateral surface area ($πrl$)
Because right cones make a right triangle with side lengths of: $h$, $l$, and $r$, you can often use the Pythagorean Theorem to solve problems.
Pyramids
Pyramids are geometric solids that are similar to cones, except that they have a polygon for a base and flat, triangular sides that meet at an apex.
There are many types of pyramids, defined by the shape of their base and the angle of their apex, but for the sake of the ACT, you only need to concern yourself with right, square pyramids.
A right, square pyramid has a square base (each side has an equal length) and an apex directly above the center of the base. The height ($h$), drawn from the apex to the center of the base, makes a right angle with the base.
Volume
$\Volume = 1/3\area\of\the\base * h$
To find the volume of a square pyramid, you could also say $1/3lwh$ or $1/3s^2h$, as the base is a square, so each side length is the same.
Spheres
A sphere is essentially a 3D circle. In a circle, any straight line drawn from the center to any point on the circumference will all be equidistant. This distance is the radius ($r$). In a sphere, this radius can extend in three dimensions, so all lines from the surface of the sphere to the center of the sphere are equidistant.
Volume
$\Volume = 4/3πr^3$
Inscribed Solids
The most common inscribed solids on the ACT math section will be "cube inside a sphere" and "sphere inside a cube." You may get another shape entirely, but the basic principles of dealing with inscribed shapes will still apply. The question is most often a test of whether you know the solid geometry principles and formulas for each shape individually well enough to be able to put them together.
When dealing with inscribed shapes, draw on the diagram they give you. If they don’t give you a diagram, make your own! By drawing in your own lines, you’ll be better able to translate the three-dimensional objects into a series of two-dimensional objects, which will more often than not lead you to your solution.
Understand that when you are given a solid inside another solid, it's for a reason. It may look confusing to you, but the ACT will always give you enough information to solve a problem.
For example, the same line will have a different meaning for each shape, and this is often the key to solving the problem.
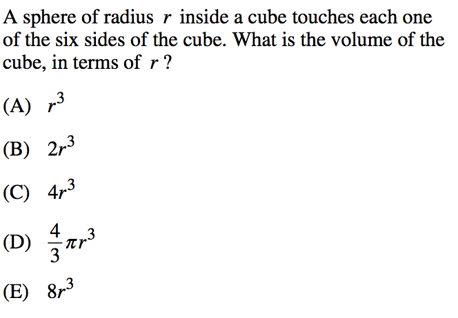
So we have an inscribed solid and no drawing. So first thing's first, make your drawing!
Now because we have a sphere inside a cube, you can see that the radius of the sphere is always half the length of any side of the cube (because a cube by definition has all equal sides). So $2r$ is the length of all the sides of the cube. Now plug $2r$ into your formula for finding the volume of a cube.
You can either use the cube volume formula:
$V = s^3$ => $(2r)^3 = 8r^3$
Or you can use the formula to find the volume of any rectangular solid:
$V = lwh$ => $(2r)(2r)(2r) = 8r^3$
Either way, you get the answer E, $8r^3$
Notice how answer B is $2r^3$. This is a trick answer designed to trap you. If you didn't use parentheses properly in your volume of a cube formula, you would have gotten $2r^3$. But if you understand that each side length is $2r$, and so that entire length must be cubed, then you will get the correct answer of $8r^3$.
For the vast majority of inscribed solids questions, the radius (or diameter) of the circle will be the key to solving the question. The radius of the sphere will be equal to half the length of the side of a cube if the cube is inside the sphere (as in the question above). This means that the diameter of the sphere will be equal to one side of the cube, because the diameter is twice the radius.
But what happens when you have a sphere inside a cube? In this case, the diameter of the sphere actually becomes the diagonal of the cube.
What is the maximum possible volume of a cube, in cubic inches, that could be inscribed inside a sphere with a radius of 3 inches?
A) $12√3$ (approximately $20.78$)
B) $24√3$ (approximately $41.57$)
C) $36√3$ (approximately $62.35$)
D) $216$
E) $1728$
First, draw out your figure.
You can see that, unlike when the sphere was inscribed in the cube, the side of the cube is not twice the radius of the circle because there are gaps between the cube's sides and the circumference of the sphere. The only straight line of the cube that touches two opposite sides of the sphere is the cube's diagonal.
So we need the formula for the diagonal of a cube:
$\side√3 = \diagonal$
$s√3 = 6$
(Why is the diagonal 6? Because the radius of the sphere is 3, so $(3)(2) = 6$)
$3s^2 = 36$
$s^2 = 12$
$s = √12$
$(√12)^3 = 12√12 = 24√3$
The answer is B), $24√3$
Though solid geometry may seem confusing at first, practice and attention to detail will have you navigating the way to the correct answer
The Take-Aways
The solid geometry questions on the ACT will always ask you about volume, surface area, or the distance between points on the figure. The way they make it tricky is by making you compare the elements of different figures or by making you take multiple steps per problem.
But you can always break down any ACT question into smaller pieces.
ACT Math Strategy: The Steps to Solving a Solid Geometry Problem
#1: Identify what the problem is asking you to find.
Is the problem asking about cubes or spheres? Both? Are you being asked to find the volume or the surface area of a figure? Both?
Make sure you understand which formulas you'll need and what elements of the geometric solid(s) you're dealing with.
#2: Draw it out
Draw a picture any time they describe a solid without providing you with a picture. This will often make it easier to see exactly what information you have and how you can use that information to find what the question is asking you to provide.
#3: Use your formulas
Once you've identified the formulas you'll need, it's often a simple matter of plugging in your given information.
If you cannot remember your formulas (like the formula for a diagonal, for example), use alternative methods to come to the answer, like the Pythagorean Theorem.
#4: Keep your information clear and double check your work
Did you make sure to label your work? The makers of the test know that it's easy for students to get sloppy in a high-stress environment and they put in "bait" answers accordingly. So make sure you label the volume for your cylinder and the volume for your cube accordingly.
And don't forget to give your answer a double-check if you have time! Does it make sense to say that a box with a height of 20 feet can fit inside a box with a volume of 15 cubic feet? Definitely not! Make sure all the elements of your answer and your work are in the right place before you finish.
Follow the steps to solving your solid geometry problems and you'll get that gold
Solid geometry is often not as complex as it looks; it is simply flat geometry that has been taken into the third dimension. If you can understand how each of these shapes changes and relate to one another, you’ll be able to tackle this section of the ACT with greater ease than ever before.
What's Next?
Now that you've done your paces on solid geometry, it might be a good idea to review all the math topics tested on the ACT to make sure you've got them nailed down tight.
Want to get a perfect score? Check out our article on How to a 36 on the ACT Math by a 36 ACT-Scorer.
Don't know where to begin? Look no further than our articles on what is considered a good, bad, or excellent ACT score
And if you find yourself running out of time on the math section, look no further than our articles on how to stop running out of time on the ACT math.
