
Though the majority of ACT math problems use diagrams or simply ask you to solve given mathematical equations, you will also see approximately 15-18 word problems on any given ACT (between 25% and 30% of the total math section). This means that knowing how best to deal with word problems will help you significantly when taking the test. Though there are many different types of ACT word problems, most of them are not nearly as difficult or cumbersome as they may appear.
This post will be your complete guide to ACT word problems: how to translate your word problems into equations and diagrams, the different types of word problems you’ll see on the test, and how best to go about solving your word problems for test day.
What Are Word Problems?
A word problem is any problem that is based mostly or entirely on written description and does not provide you with an equation, diagram, or graph. You must use your reading skills to translate the words of the question into a workable math problem and then solve for your information.
Word problems will show up on the test for a variety of reasons. Most of the time, these types of questions act to test your reading and visualization skills, as well act as a medium to deliver questions that would otherwise be untestable. For instance, if you must determine the number of sides of an unknown polygon based on given information, a diagram would certainly give the game away!
Translating Word Problems Into Equations or Drawings
In order to translate your word problems into actionable math equations that you can solve, you’ll need to know and utilize some key math terms. Whenever you see these words, you can translate them into the proper action. For instance, the word “product” means “the value of two or more values that have been multiplied together,” so if you need to find “the product of a and b,” you’ll need to set up your equation with $a * b$.
|
Key Terms |
Mathematical Action |
|
Sum, increased by, added to, total of |
+ |
|
Difference, decreased by, subtracted from |
- |
|
Product, times |
* or x |
|
Divided by |
/ or ÷ |
|
Equals, is, are, equivalent, same |
= |
|
Is less than |
< |
|
Is greater than |
> |
|
Is less than or equal to |
≤ |
|
Is greater than or equal to |
≥ |
Let's take a look at this in action with an example problem:

We have two different cable companies that each have different rates for installation and different monthly fees. We are asked to find out how many months it will take for the cost for each company to be the "same," which means we must set the two rates equal.
Uptown Cable charges 120 dollars for installation plus 25 dollars a month. We do not know how many months we're working with, so we will have:
$120 + 25x$
Downtown Cable charges 60 dollars for installation and 35 dollars per month. Again, we don't know how many months we're working with, but we know they will be the same, so we will have:
$60 + 35x$
And, again, because we are finding the amount of months when the cost is the "same," we must set our rates equal.
$120 + 25x = 60 + 35x$
From here, we can solve for $x$, since it is a single variable equation.
[Note: the final answer is G, 6 months]

Learning the language of ACT word problems will help you to unravel much of the mystery of these types of questions.
Typical ACT Word Problems
ACT word problems can be grouped into two major categories: word problems where you must simply set up an equation and word problems in which you must solve for a specific piece of information.
Word Problem Type 1: Setting Up an Equation
This is the less common type of word problem on the test, but you’ll generally see it at least once or twice. You'll also usually see this type of word problem first. For this type of question, you must use the given information to set up the equation, even though you don’t need to solve for the missing variable.
Almost always, you’ll see this type of question in the first ten questions on the test, meaning that the ACT test-makers consider them fairly “easy.” This is due to the fact that you only have to provide the set-up and not the execution.

We consider a “profit” to be any money that is gained, so we must always subtract our costs from our earnings. We know that Jones had to invest 10 million starting capital, so he is only making a profit if he has earned more than 10 million dollars. This means we can eliminate answer choices C, D, and E, as they do not account for this 10 million.
Now each boat costs Jones 7,000 dollars to make and he sells them for 20,000. This means that he earns a profit of:
$20,000 - 7,000$
$13,000$ per boat.
If $x$ represents our number of boats, then our final equation will be:
$13,000x - 10,000,000$
Our final answer is A, $13,000x - 10,000,000$
Word Problem Type 2: Solving for Your Information
Other than the few set-up word questions you’ll see, the rest of your ACT word problem questions will fall into this category. For these questions, you must both set up your equation and solve for a specific piece of information.
Most (though not all) word problem questions of this type will be scenarios or stories covering all sorts of ACT math topics, including averages, single variable equations, and probabilities, among others. You almost always must have a solid understanding of the math topic in question in order to solve the word problem on the topic.

This question is a rare example of a time in which not every piece of given information is needed to solve the problem. For most ACT word questions, all your given information will come into play at some point, but this is not the case here (though you can use all of your information, should you so choose).
For example, we are told that 25% of a given set of jelly beans are red. 25% translates to $1/4$ because 25% is the same as $25/100$ (or $1/4$). If we are being asked to find how many jelly beans are NOT red, then we know it would be $3/4$ because 100% is the same as 1, and 1 - $1/4$ = $3/4$.
So we didn’t need to know that there were 400 jellybeans to know that our final answer is H, $3/4$.
Alternatively, we could use all of our given information and find 25% of 400 in order to find the remaining jelly beans.
$400 * {1/4}$ or $400/4$
$100$
If 100 jellybeans are red, then 400 - 100 = 300 jelly beans are NOT red. This means that the not-red jelly beans make up,
$300/400$
$3/4$ of the total number of jelly beans.
Again, our final answer is H, $3/4$
You might also be given a geometry problem as a word problem, which may or may not be set up with a scenario as well.
Geometry questions will be presented as word problems typically because the test-makers felt the problem would be too easy to solve had you been given a diagram.

The test-makers didn’t give us a diagram, so let's make ourselves one and fill it in with what we know so far.
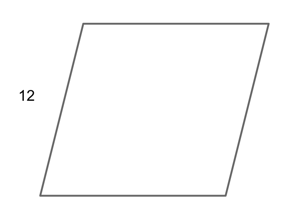
We know from our studies of parallelograms that opposite side pairs will be equal, so we know that the opposite side of our given will also be 12.

Now we can use this information to subtract from our total perimeter.
$72 - 12 - 12$
$48$
Again, opposite sides will be equal and we know that the sum of the two remaining sides will be 48. This means that each remaining side will be:
$48/2$
$24$
Now we have four sides in the pairings of 12 and 24.
Our final answer is C, 12, 12, 24, 24.

Now, how do we put our knowledge to its best effect? Let's take a look.
ACT Math Strategies for Your Word Problems
Though you’ll see word problems on a myriad of different types of ACT math topics, there are still a few techniques you can apply to solve your word problems as a whole.
#1: Draw It Out
Whether your problem is a geometry problem or an algebra problem, sometimes making a quick sketch of the scene can help you understand what, exactly, you're working with. For instance, let's look at how a picture can help you solve a ratio/division problem:

Let's start by first drawing our sandwich and Jerome's portion of it.

Now let's divvy off Kevin's portion and, by the remainder, Seth's as well.

By seeing the problem visually, we can see that the ratio of Jerome's share, to Kevin's, to Seth's will go in descending order of size. This let's us eliminate answer choices A, B, and C, and leaves us with answer choices D and E.
Just by drawing it out and using process of elimination, and without knowing anything else about ratios, we have a 50-50 shot of guessing the right answer. And, again, without knowing anything else about fractions or ratios, we can make an educated guess between the two options. Since Jerome's share doesn't look twice as large as Kevin's, our answer is probably not E.
This leaves us with our final answer D, 3:2:1.
[Note: for a breakdown on how to solve this problem using fractions and ratios instead of using a diagram and educated guessing, check out our guide to ACT fractions and ratios.]
As for geometry problems, remember—you’re often given a word problem as a word problem because it would be too simple to solve had you had a diagram to work with from the get-go. So take back the advantage and draw the picture yourself. Even a quick and dirty sketch can help you visualize the problem much easier than you can in your head and help keep all your information clear.
#2: Memorize Important Terms
If you’re not used to translating English words into mathematical equations, then ACT word problems can sound like so much nonsense and leave you floundering to set up the proper equation. Look to the chart and learn how to translate your keywords into their math equivalents. Doing so will help you to understand exactly what the problem is asking you to find.
There are free ACT math questions available online, so memorize your terms and then practice on real ACT word problems to make sure you’ve got your definitions down and can apply them to real problems.
#3: Underline and Write Out the Key Information
The key to solving a word problem is bringing together all the relevant pieces of given information and putting them in the right places. Make sure you write out all your givens on the diagram you’ve drawn (if the problem calls for a diagram) and that all your moving pieces are in order.
One of the best ways to keep all your pieces straight is to underline them in the problem and then write them out yourself before you set up your equation, so take a moment to perform this step.
#4: Pay Close Attention to Exactly What Is Being Asked of You
Little is more frustrating than solving for the wrong variable or writing in your given values in the wrong places. And yet this is entirely too easy to do when working with word problems.
Make sure you pay strict attention to exactly what you’re meant to be solving for and exactly what pieces of information go where. Are you looking for the area or the perimeter? The value of $x$ or $x + y$? Better to make sure before you start what you’re supposed to find than realize two minutes down the line that you have to solve the problem all over again.
#5: Brush Up on Any Specific Math Topic in Which You Feel Weak
You are likely to see both diagram/equation problems and word problems for any given ACT math topic on the test. Many of the topics can swing either way, which is why there are so many different types of word problems and why you’ll need to know the ins and outs of any particular math topic in order to solve its corresponding word problem. For example, if you don’t know how to properly set up a system of equations problem, you will have a difficult time of it when presented with a word problem on the topic.
So understand that solving a word problem is a two-step process: it requires you to both understand how word problems themselves work and to understand the math topic in question. If you have any areas of mathematical weakness, now is a good time to brush up on them, or else the word problem might be trickier than you were expecting.

All set? Time to shine!
Test Your Knowledge
Now to put your word problem know-how to the test with real ACT math problems.
1)

2)

3)

4)

Answers: K, C, A, E
Answer Explanations:
1) First, let us make a sketch of what we have, just so we can keep our measurements straight. We know we have two triangles, one smaller than the other, and the hypotenuse of the smaller triangle is 5.

Now our triangles are in a ratio of 2:5, so if the hypotenuse of the smaller triangle is 5, we can find the hypotenuse of the larger triangle by setting them up in a proportion.
$2/5 = 5/x$
$2x = 25$
$x = 12.5$
Our final answer is K, 12.5.
2) Because we are dealing with a hypothetical number that is increasing and decreasing based on percentage, we can solve this problem in one of two ways--by using algebra or by plugging in our own numbers.
Solving Method 1: Algebra
If we assign our hypothetical number as $x$, we can say that $x$ is increased by 25% by saying:
$x + 0.25x$
Which gives us:
$1.25x$
Now, we can decrease this value by 20% by saying:
$1.25x - (1.25x * 0.2)$
$1.25x - 0.25x$
This leaves us with:
$1x$ or 100% of our original number.
Our final answer is C, 100%.
Solving Method 2: Plugging in Numbers
Alternatively, we can use the same basic process, but make it a little simpler by using numbers instead of variables.
Let's say our original number is 100. (Why 100? Why not! Our number can literally be anything and 100 is an easy number to work with.)
So if we need to increase 100 by 25%, we first need to find 25% of 100 and then add that to 100.
$100 + (0.25)100$
$100 + 25$
$125$
Now we need to decrease this value by 20%, so we would say:
$125 - (0.2)125$
$125 - 25$
$100$
We are left with the same number we started with, which means we are left with 100% of the number we started with.
Again, our final answer is C, 100%.
3) Let's first begin by drawing a picture of our scene. We know that one vertex of the square is at (3, 0), so we can mark it on a coordinate plane.

Now, we are told that each side of the square is 3 cm long. To make life simple, we can start by marking all the possible vertexes attached to our known vertex at (3, 0) straight up, down, and side to side. If no answers match, we can then look to vertexes at different angles.

Our possible vertexes are:
(0, 0), (6, 0), 3, 3) and (3, -3)
One of our possible vertexes is at (6, 0 and this matches one of our answer choices, so we can stop here.
Our final answer is A, (6, 0).
4) We are told that Ms. Lopez throws out the lowest test score and then averages the remaining scores. Because Victor's scores are already in ascending order, we can throw out the first score of 62.
Now to find the average of the remaining 4 scores, let us add them together and then divide by the number of scores.
$(78 + 83 + 84 + 93)/4$
$338/4$
$84.5$
Our final answer is E, 84.5.
 A round of applause to your success!
A round of applause to your success!
Picture: John Morris/Flickr
The Take-Aways
Word problems comprise a significant portion of the ACT, so it’s a good idea to understand how they work and how to translate the words into a proper equation. But remember that translating your word problems is still only half the battle.
You must also supplement this knowledge of how to solve word problems with a solid understanding of the math topic in question. For example, it won’t do a lot of good if you can translate a probability word problem if you don’t understand exactly how probabilities work. So be sure to not only learn how to approach your word problems, but also hone your focus on any math topics you feel you need to improve upon. You can find links to all of our ACT math topic guides here to help your studies.
What’s Next?
Want to brush up on any of your other math topics? Check out our individual math guides to get the walk-through on each and every topic on the ACT math test.
Trying to stop procrastinating? Learn how to get over your desire to procrastinate and make a well-balanced study plan.
Running out of time on the ACT math section? We'll teach you how to beat the clock and maximize your ACT math score.
Trying to get a perfect score? Check out our guide to getting a perfect 36 on ACT math, written by a perfect-scorer.











