
Questions about both circles and various types of polygons are some of the most prevalent types of geometry questions on the ACT. Polygons come in many shapes and sizes and you will have to know them inside and out in order to take on the many different types of polygon questions the ACT has to offer.
The good news is that, despite their variety, polygons are often less complex than they look; a few simple rules and strategies are all that you need when it comes to solving an ACT polygon question.
This will be your complete guide to ACT polygons—the rules and formulas for various polygons, the kinds of questions you’ll be asked about them, and the best approach for solving these types of questions.
What is a Polygon?
Before we go to polygon formulas, let’s look at what exactly a polygon is.
A polygon is any flat, enclosed shape that is made up of straight lines. To be “enclosed” means that the lines must all connect, and no side of the polygon can be curved.
Polygons

NOT Polygons

Polygons come in two broad categories—regular and irregular. A regular polygon has all equal sides and all equal angles, while irregular polygons do not.
Regular Polygons

Irregular Polygons

A polygon will always have the same number of sides as it has angles. So a polygon with nine sides will have nine angles.
The different types of polygons are named after their number of sides and angles. A triangle is made of three sides and three angles (“tri” meaning three), a quadrilateral is made of four sides (“quad” meaning four), a pentagon is made of five sides (“penta” meaning five), etc.
Many of the polygons you’ll see on the ACT (though not all) will either be triangles or some sort of quadrilateral. Triangles in all their forms are covered in our complete guide to ACT triangles, so let’s move on to look at the various types of quadrilaterals you’ll see on the test.

Barber shop quartets, quadrilaterals—clearly the secret to success is in fours.
Quadrilaterals
There are many different types of quadrilaterals, most of which are subcategories of one another.
Parallelogram
A parallelogram is a quadrilateral in which each set of opposite sides is both parallel and congruent (equal) with one another. The length may be different than the width, but both widths will be equal and both lengths will be equal.

Parallelograms are peculiar in that their opposite angles will be equal and their adjacent angles will be supplementary (meaning any two adjacent angles will add up to 180 degrees).

Most questions that require you to know this information are quite straightforward. For example:

If we draw this parallelogram, we can see that the two angles in question are supplementary.

This means that the two angles will add up to 180 degrees. Our final answer is F, add up to 180 degrees.
Rhombus
A rhombus is a type of parallelogram in which all four sides are equal and the angles can be any measure (so long as their adjacents add up to 180 degrees and their opposite angles are equal).
Rectangle
A rectangle is a special kind of parallelogram in which each angle is 90 degrees. The rectangle’s length and width can either be equal or different from one another.

Square
If a rectangle has an equal length and width, it is called a square. This means that a square is a type of rectangle (which in turn is a type of parallelogram), but NOT all rectangles are squares.
Trapezoid
A trapezoid is a quadrilateral that has only one set of parallel sides. The other two sides are non-parallel.

Kite
A kite is a quadrilateral that has two pairs of equal sides that meet one another.

You'll notice that a lot of polygon definitions will fit inside other definitions, but a little organization (and dedication) will help keep them straight in your head.
Polygon Formulas
Though there are many different types of polygons, their rules and formulas build off of a few basic ideas. Let’s go through the list.
Area Formulas
Most polygon questions on the ACT will ask you to find the area or the perimeter of a figure. These will be the most important area formulas for you to remember on the test.
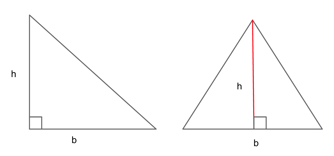
Area of a Triangle
$$a = {1/2}bh$$
The area of a triangle will always be half the amount of the base times the height. In a right triangle, the height will be equal to one of the legs. In any other type of triangle, you must drop down your own height, perpendicular from the vertex of the triangle to the base.
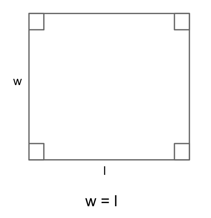
Area of a Square
$$l^2$$
Or
$$lw$$
Because each side of a square is equal, you can find the area by either multiplying the length times the width or simply by squaring one of the sides.
Area of a Rectangle
$$lw$$
For any rectangle that is not a square, you must always multiply the base times the height to find the area.
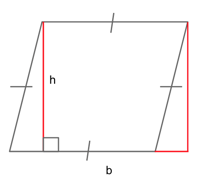
Area of a Parallelogram
$$bh$$
Finding the area of a parallelogram is exactly the same as finding the area of a rectangle. Because a parallelogram may slant to the side, we say we must use its base and its height (instead of its length and width), but the principle is the same.

You can see why the two actions are equal if you were to transform your parallelogram into a rectangle by dropping down straight heights and shifting the base.
Area of a Trapezoid
$$[(l_1 + l_2)/2]h$$
In order to find the area of a trapezoid, you must find the average of the two parallel bases and multiply this by the height of the trapezoid.

Let's take a look at this formula in action,

The trapezoid is divided into a rectangle and two triangles. Lengths are given in inches. What is the combined area of the two shaded triangles?
A. 4
B. 6
C. 9
D. 12
E. 18
If you remember your formula for trapezoids, then we can find the area of our triangles by finding the area of the trapezoid as a whole and then subtracting out the area of the rectangle inside it.
First, we should find the area of the trapezoid.
$[(l_1 + l_2)/2]h$
$[(6 + 12)/2]3$
$(18/2)3$
$(9)3$
$27$
Now, we can find the area of the rectangle.
$6 * 3$
18
And finally, we can subtract out the area of the rectangle from the trapezoid.
$27 - 18$
9
The combined area of the triangles is 9.
Our final answer is C, 9.
In general, the best way to find the area of different kinds of polygons is to transform the polygon into smaller and more manageable shapes. This will also help you if you forget your formulas come test day.
For example, if you forget the formula for the area of a trapezoid, turn your trapezoid into a rectangle and two triangles and find the area for each.
Luckily for us, this has already been done in this problem.

We know that we can find the area of a triangle by ${1/2}bh$ and we already have a height of 3.
We also know that the combined bases for the triangles will be:
$12 - 6$
6
So let us say that one triangle has a base of 4 and the other has a base of 2. (Why those numbers? Any numbers for the triangle bases will work so long as they add up to 6.)
Now, let us find the area for each triangle.
or the first triangle, we have:
${1/2}(4)(3)$
$(2)(3)$
$6$
And for the second triangle, we have:
${1/2}(2)(3)$
$(1)(3)$
3
Now, let us add them together.
$6 + 3$
9
Again, the area of our triangles together is 9.
Our final answer is C, 9.
Always remember that there are many different ways to find what you need, so don’t be afraid to use your shortcuts!
Side and Angle Formulas
Whether your polygon is regular or irregular, the sum of its interior degrees will always follow the rules of that particular polygon. Every polygon has a different degree sum, but this sum will be consistent, no matter how irregular the polygon.
For example, the interior angles of a triangle will always equal 180 degrees, whether the triangle is equilateral (a regular polygon), isosceles, acute, or obtuse.

So by that same notion, the interior angles of a quadrilateral—whether kite, square, trapezoid, or other—will always add up to be 360 degrees.

Interior Angle Sum
You will always be able to find the sum of a polygon’s interior angles in one of two ways—by memorizing the interior angle formula, or by dividing your polygon into a series of triangles.
Method 1: Interior Angle Formula
$$(n−2)180$$
If you have an n number of sides in your polygon, you can always find the interior degree sum by the formula $(n - 2)$ times 180 degrees.
Method 2: Dividing Your Polygon Into Triangles
The reason the above formula works is because you are essentially dividing your polygon into a series of triangles. Because a triangle is always 180 degrees, you can multiply the number of triangles by 180 to find the interior degree sum of your polygon, whether your polygon is regular or irregular.

As we saw, we have two options to find our interior angle sum. Let us try each method.
Solving Method 1: formulas
$(n - 2)180$
There are 5 sides, so if we plug that into our formula for $n$, we get:
$(5 - 2)180$
$3(180)$
540
Now we can find the sum of the rest of the angle measurements by subtracting our known degree measure, 50, from our total interior degrees of 540.
$540 - 50$
490
Our final answer is K, 490.
Solving Method 2: diving polygon into triangles
We can also always divide our polygon into a series of triangles to find the total interior degree measure.

We can see that our polygon makes three triangles and we know that a triangle is always 180 degrees. This means that the polygon will have a interior degree sum of:
$3 * 180$
540 degrees.
And finally, let us subtract the known angle from the total in order to find the sum of the remaining degrees.
$540 - 50$
490
Again, our final answer is K, 490.
Individual Interior Angles
If your polygon is regular, you will also be able to find the individual degree measure of each interior angle by dividing the degree sum by the number of angles. (Note: n can be used for both the number of sides and the number of angles because the number of sides and angles in a polygon will always be equal.)
${(n - 2)180}/n$
Again, you can choose to either use the formula or the triangle dividing method by dividing your interior sum by the number of angles.
Number of Sides
As we saw earlier, a regular polygon will have all equal side lengths. And if your polygon is regular, you can find the number of sides by using the reverse of the formula for finding angle measures.
A regular polygon with n sides has equal angles of 140 degrees. How many sides does the figure have?
-
6
-
7
-
8
-
9
-
10
For this question, it will be quickest for us to use our answers and work backwards in order to find the number of sides in our polygon. (For more on how to use the plugging in answers technique, check out our guide to plugging in answers).
Let us start at the middle with answer choice C.
We know from our angle formula (or by making triangles out of our polygons) that an eight sided figure will have:
$(n - 2)180$
$(8 - 2)180$
$(6)180$
1080 degrees.
Or again, you can always find your degree sum by making triangles out of your polygon.

This way you will still end up with (6)180=1080 degrees.
Now, let us find the individual degree measures by dividing that sum by the number of angles.
$1080/8$
$135$
Answer choice C was too small. And we also know that the more sides a figure has, the larger each individual angle will be, so we can cross off answer choices A and B, as those answers would be even smaller. (How do we know this? A regular triangle will have three 60 degree angles, a square will have four 90 degree angles, etc.)
Now let us try answer choice D.
$(n - 2)180$
$(9 - 2)180$
$(7)180$
1260
Or you could find your internal degree sum by once again making triangles from your polygons.

Which would again give you $(7)180 = 1260$ degrees.
Now let’s divide the degree sum by the number of sides.
$1260/9$
$140$
We have found our answer. The figure has 9 sides.
Our final answer is D, 9.
Number of Diagonals
$${n(n - 3)}/2$$
It is common for the ACT to ask you about the number of distinct diagonals in a polygon. Again, you can find this information using the formula or by drawing it out (or a combination of the two).
This is basically the same as dividing your polygon into triangles, but they will be overlapping and you are counting the number of lines drawn instead of the number of triangles.

Method 1: formula
In order to find the number of distinct diagonals in a polygon, you can simply use the formula ${n(n - 3)}/2$, wherein $n$ is the number of sides of the polygon.
Method 2: drawing it out
The reason the above formula works is a matter of logic. Let’s look at an octagon, for example.
You can see that an octagon has eight angles (because it has eight sides). If you were to draw all the diagonals possible from one particular angle, you could draw five lines.

You will always be able to draw n−3 lines because one of the angles is being used to form all the diagonals and the lines to the two adjacent angles make up part of the perimeter of the polygon and are therefore NOT diagonals. So you can only draw diagonals to n−3 corners.
Now, let’s mark another angle’s series of diagonals.

You can see that none of these diagonals overlap, BUT if we were to draw the diagonals from an opposite corner, we would have multiple overlapping diagonals.
The adjacent angles will not overlap, but the opposite ones will. This means that there will only be half as many diagonals as the total number of angles multiplied by their possible diagonals (in other words half of n(n−3).
This is why our final formula is:
${n(n - 3)}/2$
This is all the angles multiplied by their total number of diagonals, all divided by half so that we do not get overlapping diagonal lines.
(Note: of course an alternative to using any form of the formula is to simply draw out your diagonals, making sure to be very very careful to not create any overlapping diagonal lines.)

Just make sure you don't dizzy yourself keeping track of all your angles and diagonals.
Typical Polygon Questions
Now that we’ve been through all of our polygon rules and formulas, let’s look at a few different types of polygon questions you’ll see on the ACT.
About half of ACT polygon questions you’ll see will involve diagrams and about half will be word problems. Most all of the word problems will involve quadrilaterals in some form or another.
Typically, you will be asked to find one of three things in a polygon question:
-
The measure of an angle (or the sum of two or more angles)
-
The perimeter of a figure
-
The area of a figure
Let’s look at a few real ACT math examples of these different types of questions.
1. Finding the measure of an angle

We know that we can find the degree measure of a regular polygon by finding their total number of degrees and dividing that by the number of sides/angles. So let us find the sum of the interior degrees of our pentagon.

A pentagon can be divided into three triangles, so we know that it has a total of:
3(180)
540 degrees.
If we divide this number by the number of sides/angles in a pentagon, we can see that each angle measure is:
$540/5$108
Now, we also know that every straight line is 180 degrees. This means that we can find the exterior angles of the pentagon by subtracting the interior angles from 180.
$180 - 108$
72

We also know that a triangle's interior degrees always add up to 180, so we can find our final angle by subtracting our two known angles from 180.
$180 - 72 - 72$
36
Our final answer is C, 36.
2: Finding the perimeter of a figure

We know that a square has, by definition, all equal sides.
Because DC is 6, that means that ED, EB, and BC are all equal to 6 as well.
We also know that an equilateral triangle has all equal sides. Because EB equals 6 and is part of the equilateral triangle, EB, AE, and AB are all equal to 6 as well.
And, finally, the perimeter of the figure is made up of lines DE, EA, AB, BC, and CD. This means that our perimeter is:
6 + 6 + 6 + 6 + 6
30
Our final answer is C, 30.
3: Using or finding the area of the figure

We know that the area of a rectangle is found by multiplying the length times the width, and we also know that a rectangle has two paris of equal sides. So we need to find measurements for the sides that, in pairs, add up to 24 and, when multiplied, will make a prouct of 32.
One way we can do this is to use the strategy of plugging in answers. Let us, as usual when using this strategy, start with answer choice C.
So, if we have a short side length of 3, we need to double it to find how much the short sides contribute to the total perimeter.
$3 * 2$
6
If we subtract this from our total perimeter, we find that the sum of our longer sides are:
$24 - 6$
18
Which means that each of the longer sides is:
$18/2$
9
Now, if one side length is 3 and the other is 9, then the area of the rectangle will be:
$3 * 9$
27
This is too small to be our area.
We need the shorter side lengths to be longer than 3 so that the product of the length and the width will be larger. Let us try option J instead.
If we have two side lengths that each measure 4, they will add a total of:
$4 * 2$
8
Now let us subtract this from the total perimeter.
$24 - 8$
16
This is the sum of the longer side lengths, which means we must divide this number in half to find the individual measures.
$16/2$
8
And finally, let us multiply the length times the width to find the area of the rectangle.
$8 * 4$
32
These measurements fit our requirements, which means that the shorter sides must each measure 4.
Our final answer is J, 4.

Now let's look at the strategies for success for your polygon questions (as well as what to avoid doing).
How to Solve a Polygon Question
Now that we’ve seen the typical kinds of questions you’ll be asked on the ACT and gone through the process of finding our answers, we can see that each solving method has a few techniques in common.
In order to solve your polygon problems most accurately and efficiently, take note of these strategies:
#1: Break up figures into smaller shapes
Don’t be afraid to write all over your diagrams. Polygons are complicated figures, so always break them into small pieces when you can. Break them apart into triangles, squares, or rectangles and you’ll be able to solve questions that would be impossible to figure out otherwise.
Alternatively, you may need to expand your figures by providing extra lines and creating new shapes in which to break your figure. Just always remember to disregard these false lines when you’re finished with the problem.

If we create and expand new lines in our figure, we can make our lengths and sides a little more clear.

We can also see why this works because our red lines are essentially extensions of the perimeter branching outwards in order to give us a clearer picture.

Now, we know that, because the bottom-most horizontal line is equal to 20, the sum of all the other horizontal lines is also equal to 20.
We can also see that all the vertical lines will add up to:
12 + 8 + 8 + 12
This means that our total perimeter will be:
20 + 20 + 12 + 12 + 8 + 8
80
Our final answer is B, 80.
#2: Use your shortcuts
If you don’t feel comfortable memorizing formulas or if you are worried about getting them wrong on test day, don’t worry about it! Just understand your shortcuts (for example, remember that all polygons can be broken into triangles) and you’ll do just fine.
#3: When possible, use PIA or PIN
Because polygons involve a lot of data, it can be very easy to confuse your numbers or lose track of the path you need to go down to solve the problem. For this reason, it can often help you to use either the plugging in answer strategy (PIA) or the plugging in numbers strategy (PIN), even though it can sometimes take longer (for more on this, check out our guides to PIA and PIN).
#4: Keep your work organized
There is a lot of information to keep track of when working with polygons (especially once you break the figure into smaller shapes). It can be all too easy to lose your place or to mix-up your numbers, so be extra vigilant about your organization and don’t let yourself lose a well-earned point due to careless error.
 Before you go ahead and put your polygon knowledge to the test, take a moment to bask in some much-needed Cuteness.
Before you go ahead and put your polygon knowledge to the test, take a moment to bask in some much-needed Cuteness.
Test Your Knowledge
Now, let's test your knowledge on polygons with some real SAT math examples.
1.

2.

3.

4.

Answers: D, C, G, G
Answer Explanations:
1. In order to find the number of distinct diagonals, we can, as always, either use our diagonal formula or be very (very) careful to draw our own. Let us try both methods.
Method 1: formula
${n(n - 3)}/2$
We have a hexagon, so there are 6 sides. We can therefore plug 6 in for n.
${6(6 - 3)}/2$
$6(3)/2$
$18/2$
$9$
There will be 9 distinct diagonals.
Our final answer is D, 9.
Method 2: drawing it out
If we draw our own diagonals, we can see that there are still 9 diagonals total. We can color-code these lines here, but you will not have that option on the test, so make sure you are both able to draw out all your diagonals and not count repeat lines.

When done correctly, we will have 9 distinct diagonals in our hexagon.
Our final answer is D, 9.
2. We know that, by definition, a parallelogram has two pairs of equal sides. So if one side measures 12, then at least one of the other three sides must also measure 12.
So let us first subtract our pair of 12-length sides from our total perimeter of 72.
$72 - 12 -12$
48
The remaining pair of sides will have a sum of 48. We also know that the remaining pair of sides must be equal to one another, so let us divide this sum in half in order to find their individual measures.
$48/2$24
This means that our parallelogram will have side measures of:
12, 12, 24, 24
Our final answer is C.
3. We are told that each of these rectangles is a square, which means that the side lengths for each square will be equal. We also know that, in order to find the area of a square, we can simply square (multiply a number by itself) one of the sides.
So, if the larger square has an area of 50 square centimeters, that means that one of the side lengths squared must be equal to 50. In other words:
$s^2 = 50$
$s =√50$
$s =√25 *√2$
$s = 5√2$
(For more info on how to manipulate roots and squares like this, check out our guide to ACT advanced integers.)
So now we know that the length of each of the sides of the larger square is $5√2$.
We also know that the area of the smaller square is 18 and that the length of one of the sides of the shorter square is the length of the side of the larger square, minus x.
img src="https://cdn2.hubspot.net/hubfs/360031/body_square_example.png" alt="body_square_example" style="display: block; margin-left: auto; margin-right: auto; width: 212px;" width="212">
So let us find x by using this information.
$(5√2 - x)^2 = 18$
$5√2 - x =√18$
$5√2 - x =√9 *√2$
$5√2 - x = 3√2$
$-x = -2√2$
$x = 2√2$
We have successfully found the length of $x$.
Our final answer is G,$2√2$.
4. We have a few different ways to solve this problem, but one of the easiest is to use the strategy of plugging in our own numbers. This will help us to visualize the lengths and areas much more solidly.
So let us imagine for a minute that the longest length of our rectangle is 12 and the shorter side is 4. (Why those numbers? Why not! When using PIN, we can choose any numbers we want to, so long as they do not contradict our given information. And these numbers do not, which means we're good to go.)

Now, to make life even simpler, let us divide our rectangle in half and just work with one half at a time.

Now, because we have divided our rectangle exactly in half (and we know that we did this because we are told that F and E are both midpoints of the longest side of our rectangle), we know that BF must be 6.

Now we have four triangles, three of which are shaded. In order to find the ratio of unshaded area to shaded area, let us find the areas of each of our triangles.
To find the area of a triangle, we know we need:
${1/2}bh$If we take the triangle on the left, we already know that our base is 4. We also know that the height must be 3. Why? Because point G is directly in the middle of our rectangle, so the height will be exactly half of the line BF.

This means that our left-most triangle will have an area of:
${1/2}bh$
${1/2}(4)(3)$
$(2)(3)$
$6$
Now, we know that our right-most triangle (the unshaded triangle) will ALSO have an area of 6 because its height and base will be exactly the same as our left triangle.
So let us find the areas of our top and bottom triangles.
Again, we already have a given value for our base (in this case 6) and the height will be exactly half of the line BA.

This means that the area of our top triangle (as well as our bottom triangle) will be:
${1/2}bh$
${1/2}(6)(2)$
$(3)(2)$
$6$
Both the left and the top-most triangles have an area of 6, which means that ALL the triangles have equal areas.
There is 1 unshaded triangle and 3 shaded triangles. This means that the ratio of unshaded to shaded triangles is 1:3.
We also know that this will be the same ratio if we were to complete the problem for the other half of the rectangle. Why? We cut the shape exactly in half, so the ratio of all the unshaded triangles to shaded triangles will be:
2:6
Or, again:
1:3
Our final answer is G, 1:3.

A little practice, a little flare, and you've got the path down to all your right answers.
The Take Aways
Once you internalize the few basic rules of polygons, you’ll find that these questions are not generally as difficult as they may appear at first blush. You may come across irregular polygons and ones with many sides, but the basic strategies and formulas will always be the same.
Remember your strategies, keep your work well organized, and know your key definitions, and you will be able to take on even the most difficult polygon questions the ACT can throw at you.
What’s Next?
You've mastered polygons and now you're raring to take on more (we're guessing). Luckily for you, there are so many more math topics to cover! Take a glance through all the math topics that will appear on the ACT to make sure you've got them locked down tight. Then go ahead and check out our ACT math guides to brush up on any topics you might be rusty on. Feeling nervous about circle questions? Roots and exponents? Fractions and ratios? Whatever you need, we have the guide for you.
Want to learn some of the most useful math strategies on the test? Check out our guides to plugging in answers and plugging in numbers to help you solve questions that may have had you scrambling before.
Want to get a perfect score? Look no further than our guide to getting a perfect 36 on ACT math, written by a perfect-ACT-scorer.











