Trigonometry is the branch of math that deals with right triangles and the relationships between their sides and angles. (The word "trig" is related to the word "triangle," to help you remember.)
There will generally be around 4-6 questions questions on the ACT that deal with trigonometry (the official ACT guidelines say that trigonometry problems make up 7% of the test). They may seem complicated at first glance, but most of them boil down to a few simple concepts.
This article will be your comprehensive guide to the trigonometry you’ll need to know for the ACT. We’ll take you through the meaning of trigonometry, the formulas and understandings you’ll need to know, and how to tackle some of the most difficult ACT trig problems.
What is Trigonometry and How Do I Use It?
Trigonometry studies the relationships between the sides and angles of right triangles. The ratios between the measures of the sides of a right triangle and the measures of its angles are consistent, no matter how large or small the triangle.
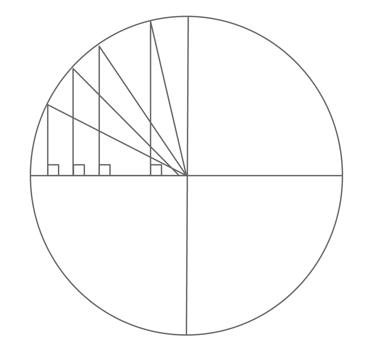
If you know one side measure and one non-90° angle of the right triangle, you will be able to determine the rest of the triangle’s sides and angles. And if you have the lengths of two sides of a right triangle, you will be able to find the measure of all the interior angles.
If we have two side lengths, we can use the Pythagorean theorem to find the third.
So $12^2+14^2=c^2$
$c^2=340$
$c=√340$ or $c=2√85$
But what if we only have one side length and the measure of one of the (non-ninety degree) angles?
Even though we only have the length of one side, we can still find the others using trigonometry because we have the measure of one of the acute angles.
So here, we could say $sin 34° =12/\hypotenuse\$
So $\hypotenuse\ = 12/{sin 34°}$
Don't worry if this doesn't make sense to you yet! We'll break down each step as we go further into the guide.
(Note: to find the actual degree measure of an angle using two side lengths, you would have to perform an inverse function calculation (also called an "arc" function). But DON’T WORRY—the ACT will never actually make you do this! In terms of your ACT math prep, understand that the test will only ever ask you to calculate far enough to say, for example, "$Cosinex=4/5$." You will never have to find the actual angle measure of x on the ACT.
The way we find these measures is by understanding the ratio of certain sides of the triangle to their corresponding angles. These are called trigonometric functions and there are three that you should memorize for the ACT: sine, cosine, and tangent. The easiest way to understand this is through the mnemonic device SOH, CAH, TOA, which we will discuss in a bit.>/p>
Trigonometry is widely used in navigation as well as in calculating heights and distances. (In case you were wondering if you ever needed trig in real life.)
The Most Common ACT Trig Questions
The trigonometry questions on the ACT will fall into just a few different categories. We have provided a few real ACT math examples to demonstrate each concept.
#1: Finding the sine, cosine, or tangent (or, more rarely, cosecant, secant, or cotangent) of an angle from a given right triangle diagram.
#2: Finding the sine, cosine, or tangent of a right triangle from a word problem.
Alex props up a ladder against a wall. The ladder makes an angle of 23° from the ground. If the ladder is 10 feet long, what is the expression for finding the distance the foot of the ladder is from the wall?
A. 10 $tan23°$
B. 10 $sin23°$
C. 10 $cos23°$
D. $cos{10/23}$
E. $sin{10/23}$
#3: Finding the sine, cosine, or tangent (or, more rarely, cosecant, secant, or cotangent) of an angle from a given sin, cos, or tan and a range in which the angle falls.
If $tanΘ=3/4 \and 180°<Θ<270°$, what is $sinΘ$?
A. $4/3$
B. $-4/3$
C. $-3/4$
D. $3/5$
E. $-3/5$
#4: Finding the period or amplitude of a graph.
What is the amplitude of the graph?
A. 1
B. 2
C. π
D. 2π
E. 0
#5: Law of sines or law of cosines question.
For a question like this, they will give you the formulas for the law of sines or law of cosines, so you don’t have to worry about memorizing them. Having the formula won’t help you much, however, if it looks or sounds like gibberish to you. As you go through this guide, do the ACT math practice questions we've provided, and familiarize yourself with the trigonometry language used in these questions, they will become much easier to solve.
We’ll go through how to solve each of these kinds of problems, but this gives you a sense of what the ACT trig problems will look like on the test.
SOH, CAH, TOA
Remember this famous mnemonic? It will save your life. Let's go through each one.
SOH (Sine)
Sine is a function where the sine (also called "sin") value of an angle theta can be found by using the ratio of the side of the triangle opposite the angle theta over the hypotenuse of the triangle.
SOH: Sin $Θ$ = Opposite side of triangle/Hypotenuse of triangle
So in this triangle, $sinΘ=b/c$ because the side opposite the angle $Θ$ is b and the hypotenuse is c.
CAH (Cosine)
Cosine is a function where the cosine (also called "$cos$") value of an angle theta ($Θ$) can be found by using the ratio of the side of the triangle adjacent to the angle $Θ$ (that is not the hypotenuse) over the hypotenuse of the triangle.
CAH: Cos $Θ$ = Adjacent side of triangle/Hypotenuse of triangle
Note: adjacent means the side of the triangle that is touching the angle/helps to create the angle $Θ$.
In this same triangle, $cosΘ=a/c$ because the side adjacent the angle $Θ$ is a and the hypotenuse is c.
TOA (Tangent)
Tangent is a function where the tangent (also called "tan") value of an angle theta can be found by using the ratio of the side of the triangle opposite the angle theta over the adjacent side of the triangle to theta (that is not the hypotenuse).
TOA: Tan $Θ$ = Opposite side of triangle/Adjacent side of triangle.
In this same triangle, $tanΘ=b/a$ because the side opposite the angle $Θ$ is b and adjacent side is a.
Now that you are familiar with your mnemonic devices, you can put together questions with multiple steps. For example, a slightly more difficult question may look something like this:
You are given the lengths of two sides of the triangle but need the length of the third side to solve the problem.
Don’t forget that this is a right triangle and you can use the Pythagorean theorem to find the length of the third side!
So $2^2+x^2+5^2$
$x^2=21$
$x=√21$
Now that you have the measure of the third side, you can find $tanB$.
$TanB=\Opposite/\Adjacent$
$TanB=√21/2$
So the answer is F, $√21/2$
Which Sides are Opposite or Adjacent?
The hypotenuse of a triangle always stays the same, but the sides opposite or adjacent switch depending on the angle of focus.
For example, if you’re trying to find the $sin$ of angle $γ$, you would use the ratio of $b/c$; if you’re trying to find the sin of angle $ξ$, you would use the ratio of $a/c$.
How Do I Use These Ratios?
For the purposes of the ACT, you will either be given two side lengths, which means your final answer would look like:
$Sin Θ = \opposite/\hypotenuse$
Here, you find the length of the third side using the Pythagorean theorem.
So $10^2+x^2=12^2$
$x^2=44$
$x=√44$
Now $sin$ = $\opposite/\hypotenuse$, so $sinM=√44/12$.
So the answer is K.
No need to find the degree measure (arcsine or inverse sine) of angle M on your calculator—this is as far as you need to go.
You may also be given the value of the angle and the side length of the denominator of your ratio. When this happens, manipulate the equation as you would algebraic equation and multiply the opposite side by the denominator.
$sin Θ = \opposite/\hypotenuse$
$hypotenuse$*sinΘ =$ opposite
Since you're being asked for the length of the boat to the dock and this side is opposite the 52° angle, you know you will either need sin or tan (cos uses adjacent and hypotenuse, not opposite).
You are also given an adjacent length, 30 miles, so you will be using tan. (You can tell this side is adjacent because the side opposite the 90° angle is the hypotenuse, so 30 miles must be another leg of the triangle).
$tanΘ=\opposite/\adjacent$
So $tan52°=x/30$
30 $tan52°=x$
So the answer is F, the length of the boat to the dock is 30 tan 52°.
And again with the word problem from earlier.
Alex props up a ladder against a wall. The ladder makes an angle of 23° from the ground. If the ladder is 10 feet long, what is the expression for finding the distance the foot of the ladder is from the wall?
A. 10 $tan23°$
B. 10 $sin23°$
C. 10 $cos23°$
D. $cos10/23$
E. $sin10/23$
First, draw your picture to more easily visualize what is being asked.
So we have the measure between the ladder and the ground of $23°$. We are also working with the lengths of the adjacent side of the triangle and the hypotenuse. This means we will need cosine, as $cosΘ=\opposite/\hypoteneuse$
So $cos23°=\adjacent/10$ (Why 10? The ladder is 10 feet long)
This becomes 10 $cos23°=\adjacent$
So the answer is C, 10 $cos23°$
Will I Have to Find the Measure of an Angle?
The short answer is: no, you won't be asked to find exact measure of an angle degree using trigonometry. The longer answer is: no, you won't be asked to find the measure of an angle, but it's important to know it's done.
To get the actual degree measure of theta (Θ), you would have to perform an inverse (also called "arc") function. This would transform your equation from, for example:
$SinΘ=x/y$
$Θ=sin^{−1}(x/y)$
Although you will never be asked to find the $arctan$, $arcsin$, or $arccos$ of an angle to solve for the actual angle measure degree, it is important for you to understand how these equations are manipulated to get to the right ACT answer.
Because we know that $tan^{−1}(a/b)$ is the arctan, we know that it means we can re-write it as $tanΘ=a/b$
We also know that $tanΘ=\opposite/\adjacent$
This means that, for the angle $Θ$, a is the opposite and b is the adjacent.
We also know that $cosΘ=\adjacent/\hypoteneuse$
Because we already discovered that b is the adjacent, it means that the answer is D, $b/{√(a^2+b^2)}$
When are Sin, Cos, and Tan Positive or Negative?
Depending on where the triangle is positioned in two dimensional space, the sin, cos, and tan values will be negative or positive.
There are four quadrants in two dimensional space and they are split along the x and y axes.
- In quadrant I, both x and y are positive.
- In quadrant II, x is negative and y is positive
- In quadrant III, both x and y are negative
- And in quadrant IV, x is positive and y is negative
Just like with x and y values, sin, cos, and tan are either positive or negative depending on the quadrant the triangle/angle is in.
- In quadrant I, all are positive
- In quadrant II, sin is positive and both cos and tan are negative
- In quadrant II, tan is positive and both sin and cos are negative
- In quadrant IV, cos is positive and both sin and tan are negative
A good way to memorize this is by the mnemonic acronym ASTC—All Students Take Chemistry—to see which of the functions is positive, depending on the quadrant.
So All are positive in quadrant I, Sin is positive in quadrant II, Tan is positive in quadrant III, and Cos is positive in quadrant IV
If $tanΘ=3/4$ and $180°<Θ<270°$, what is $sinΘ$?
A. $4/3$
B. $−4/3$
C. $-3/4$
D. $3/5$
E. $-3/5$
To solve this problem, first complete the side lengths of the triangle using the Pythagorean theorem (or using your knowledge of 3-4-5 triangles).
$Tan Θ = \opposite/\adjacent$, so we know that 3 is our opposite and 4 is our adjacent. This makes our hypotenuse unknown.
$3^2+4^2=c^2$
$c^2=25$
$c=5$
So our hypotenuse is 5.
We know that $sin Θ = \opposite/\hypotenuse$. So $sinΘ=3/5$.
But wait! We're not done. Because they told us that $Θ$ lies between $180°$ and $270°$, we know that the sin value of $Θ$ is negative. According to ASTC, only the tan of angle $Θ$ will be positive between $180°$ and $270°$.
So our final answer is E,$-3/5$
Secondary Trig Functions
On rare occasions on the ACT, you will be asked to give one of the secondary trig functions. These are cosecant, secant, and cotangent. These will come up on a maximum of one question per test.
You might notice that they sound similar to the primary trig functions you learned above. In fact, these secondary functions are the reciprocal (reversal) of sin, cos, and tangent.
To help you remember which is which, look to the third letter of the each word:
- Cosecant = reciprocal of sine
- Secant = reciprocal of cosine
- Cotangent = reciprocal of tangent
Cosecant
Cosecant is the reciprocal of sine. $Cosecant Θ = \hypotenuse/\opposite$
Secant
Secant is the reciprocal of cosine. $Secant Θ = \hypotenuse/\adjacent$
Cotangent
Cotangent is the reciprocal of tangent. $Cotangent Θ = \adjacent/\opposite$
Useful Formulas with Sin, Cos, and Tan
There are two formulas that will appear occasionally on the ACT. If you feel that you cannot possibly memorize any more trigonometry, do not worry about memorizing these—they will only ever come up on a maximum of one question per test.
But if you want to get every last point possible, then these would be useful for you to memorize.
$Sin^2{Θ}+cos^2{Θ}=1$
Whenever you see $sin^2{Θ}+cos^2{Θ}$, immediately replace it with 1. This will often make problems much simpler and therefore easier to solve.
You can also manipulate the equation around just as you would any other algebraic equation.
So $cos^2{Θ}=1-sin^2{Θ}$, and $sin^2{Θ}=1-cos^2{Θ}$
They told us that $x$ is between 0 and $π/2$ radians, so we know that both sin and cos are positive (because it is in quadrant I).
We also know that $Sin^2{Θ}+cos^2{Θ}=1$ which means that $sin^2{Θ}=1-cos^2{Θ}$.
So if we square the first fraction (to get rid of the square root sign), we would have:
$({√{1-cos^2{x}}}/{sinx})^2$
$(1-cos^2{x})/(sin^2{x})$
Because $1−cos^2{Θ}$ is equal to $sin^2{Θ}$, we can replace our $1−cos^2{x}$ with $sin^2{x}$
This gives us $(sin^2{x})/(sin^2{x})$, which equals 1.
We can do the exact same process to the second fraction:
$({√{1-sin^2{x}}}/{cosx})^2$
$(1-sin^2{x})/(cos^2{x})$
$(cos^2{x})/(cos^2{x})$, which also equals 1.
So then we have 1 + 1 = 2
The final answer is H, 2.
$$(sinΘ)/(cosΘ)=tanΘ$$
This equation makes sense logically if you think about it with a diagram. Say you have a triangle that looks like this
$Sin Θ$ would be $5/13$. $Cos Θ$ would be $12/13$. $Tan Θ$ would be $5/12%.
You could also say $tanΘ={sinΘ}/{cosΘ}={5/14}/{12/13}=(5/13)(13/12)=65/156$ (you could also just cancel out both 13s to make it simpler) = $5/12$
Graphing Trig Functions
The ACT will not ask you to graph a trig function, but you do need to recognize what each function looks like as a graph.
Sine
The sine graph crosses through the origin in a wave pattern. It always rises after $x = 0$, after it crosses the origin.
It is an "odd" function because it is not symmetrical about the y-axis.
Cosine
The cosine graph is similarly "wavy" but it does not cross the origin. It descends after $x = 0$.
It might help you to remember that cosine descends after x = 0 by thinking that "co is low"
Cosine is an "even" function because it is symmetrical about the y-axis. This means that for all values of $x$, $f(x) = f(-x)$.
For example, in the graph above, $y = 0.7$ both when $x = 1$ and when $x = -1$
Sometimes all the question will ask is for you to identify if a graph is even or odd or if a graph is sin or cos. This will be an easy point for you to get if you can remember the basic elements of trig graphs.
Though you can figure this question out from the information given, it will take far less time if you can recognize that the graph is a cosine graph and is therefore even. And on the ACT, time is limited and valuable.
Tangent
The tangent graph looks very different than the sin and cos graphs—you just have to be able to recognize the tangent graph when you see it.
Periods and Amplitudes
The ACT will sometimes ask you to find the period or the amplitude of a sine or cosine graph.
Period
The period of a graph is the distance along the x-axis at which point the graph starts to repeat. Find the distance along the x-axis where the point returns to where it started after making a complete cycle.
The period of the sine graph here is 2π. It has to go both up and down before finally returning to $y = 0$.
The period of the cosine graph here is also 2π. It must go down and then back up to return to where it began at $y = 1$.
Amplitude
The amplitude of a graph is its height from the x-axis, the distance between its highest $y$-value and $x = 0$.
So to use the same graph as above:
Both the sine and the cosine have an amplitude of 1 (and, again, a period of 2π).
Radians
Radians are another (more accurate) way to measure a distance around a circle, rather than using degrees. Instead of degrees, radians are expressed in terms of π (and fractions of π).
If you have a complete circle, that is 360 degrees. It is also 2π radians.
Why 2π radians? Well, think of the formula for the circumference of a circle. C=2πr. If your radius is 1, then your circumference is 2π, which is the same as your radian measure.
A circle that has a radius of 1 and is centered at the origin is called the "unit circle." It is convenient to think about radians by situating them on a unit circle.
So if you have a half circle, it is 180° or π radians.
And so on. 90° is $π/2$ radians, 270° is $(3π)/2$ radians.
To convert degrees to radians, it is easiest to use the conversion between 180° and π.
Convert 45° to radians => $(45){π/180}=π/4$ radians
Convert $(3π)/4$ radians to degrees => ${(3π)/4}(180/π)$=135°
Steps to Approaching a Trig Question
So let’s review how to break down a trig question
#1: Identify if the problem requires trigonometry. You can tell that the problem will require trig when:
- The problem mentions sin, cos, or tan in the question or in the answer options
- The problem gives you a diagram or describes a right triangle and then asks you to find a value that cannot be found by using the pythagorean theorem alone.
- As we saw in this problem earlier—you may use the pythagorean theorem in a trigonometry problem, but you cannot solve a trig problem by only using the pythagorean theorem.
- The problem shows you a "wavy" graph along the x and y axis
- The problem asks for a graph’s period or amplitude
#2: Remember SOH, CAH, TOA.
The vast majority of ACT trig questions will just require you to plug in values into the SOH, CAH, TOA acronyms to find your sine, cosine, or tangent values
#3: Know how to manipulate SOH, CAH, TOA if need be.
Trig functions can be manipulated just like any algebraic expression.
So if you have $cos40°=x/18$, the answer becomes 18 $cos40°=x$
And if you have $sin^{−1}(10/23)=Θ$, you could also say $sinΘ=10/23$
If you have $(sinΘ)/(cosΘ)=tanΘ$, it can become $(sinΘ)=(tanΘ)(cosΘ)$
And if you remember that $sin^2{Θ}+cos^2{Θ}=1, then you can say $1−cos^2{Θ}=sin^2{Θ}, etc.
#4:. Remember what the graphs of sine, cosine, and tangent look like.
And know that:
Period = horizontal distance
Amplitude = vertical distance
#5: Celebrate, because you’ve completed your ACT trig questions!
The Take-Aways
Although trigonometry problems may look intimidating, most every ACT trig question can be solved if you know the basic trig building blocks.
To make the most of your ACT math prep, remember these three trig concepts: SOH, CAH, TOA, how to manipulate your equations, and how to recognize your function graphs. If you can remember these, you will find yourself solving most every trig question the ACT can throw at you.
What's Next?
Want more ACT math strategies and guides? Review our article on all the math topics tested on the ACT to make sure you've got them nailed down tight. Do you know your ACT solid geometry? Be sure to brush up if you're looking for every last point.
Want to get a perfect ACT Math score? Check out our article on How to a 36 on the ACT Math Section by a 36 ACT-Scorer.
Feeling overwhelmed? Don't know where to begin? Look no further than our articles on what is considered a good, bad, or excellent ACT score. Don't know what days the ACT is offered? Check out our complete list of ACT test dates to find the right one(s) for your schedule.
And if you find yourself running out of time on the math section, look no further than our article on how to stop running out of time on the ACT math.
