You likely had your first taste of working with fractions sometime in elementary school, though it's probably been a while since you've had to deal with how they shift, change, and interact with one another. To refresh, fractions and ratios are both used to represent pieces of a whole. Fractions tell you how many pieces you have compared to a potential whole amount (3 red marbles in a bag of 5, for example), while ratios compare pieces to each other (3 red marbles to 2 blue marbles) or, more rarely, pieces to the whole amount (again, 3 red marbles in 5 total).
If this sounds complicated to you right now, don’t worry! We will go through all the principles behind fractions and ratios in this guide. If this seems easy to you right now, definitely check out the practice problems at the end of the guide to make sure you have mastered all the different kinds of fraction and ratio problems you’ll see on the test. The SAT likes to present familiar concepts in unfamiliar ways, so don’t let your mastery of fractions lead you to make assumptions about how you’ll see fractions and ratios on the test.
No matter how comfortable you are (or are not) with fractions and ratios right now, this guide is for you. Here, we will go through the complete breakdown of fractions and ratios on the SAT—what they mean, how to manipulate them, and how to answer the most difficult fraction and ratio problems on the SAT.
This Guide
This guide is seperated into two distinct categories—everything you need to know about fractions and everything you need to know about ratios. For each section, we will go through the ins and outs of what fractions and ratios mean as well as how to manipulate and solve the different kinds of fraction and ratio problems you'll see on the SAT.
We will also breakdown how you can tell when an SAT problem requires a ratio or a fraction and how to set up your approach these kinds of problems. At the end, you will be able to test your knowledge on real SAT math questions.
The more you prep for the SAT, the more your brain can be Swiss-army-knife-ready for any question the test can throw at you.
What are Fractions?
$${\a \piece}/{\the \whole}$$
Fractions are pieces of a whole. They are expressed as the amount you have (the numerator) over the whole (the denominator).
A pizza is divided into 8 pieces. Kyle ate 3 pieces. What fraction of the pizza did he eat?
He ate $3/8$ths of the pizza. 3 is the numerator (top number) because he ate that many pieces of the whole, and 8 is the denominator (bottom number) because there are 8 pieces total (the whole).
Math is always more fun when it's delicious.
Special Fractions
A number over itself equals 1
$3/3=1$
$10/10=1$
$(a+b)/(a+b)=1$
A whole number can be expressed as itself over 1
$5=5/1$
$22/1=22$
$(a+b)/1=a+b$
0 divided by any number is 0
$0/17=0$
$0/(a+b)=0$
There is one exception to this rule:
$0/0=\undefined$. The reason for this lies in the next rule.
Any number divided by 0 is undefined
Zero cannot act as a denominator. For more information on this check out our guide to advanced integers. But for now all that matters is that you know that 0 cannot act as a denominator.
Reducing Fractions
If both the numerator and the denominator have a common factor (a number they can both be divided by), then the fraction can be reduced. For the purposes of the SAT, you will need to reduce your fractions to get to your final answer.
To reduce a fraction, you must divide both the numerator and the denominator by the same amount. This keeps the fraction consistent and maintains the proper relationship between numerator and denominator.
If your fraction is $3/12$, then it can be written as $1/4$. Why? Because both 3 and 12 are divisible by 3.
$3/3=1$ and $12/3=4$.
So your final fraction is $1/4$
Now let's figure out how to perform the four basic math functions on fractions.
Adding or Subtracting Fractions
You can add or subtract fractions as long as their denominators are the same. To do so, you keep the denominator consistent and simply add the numerators.
$4/15+2/15=6/15$
But you CANNOT add or subtract fractions if your denominators are unequal.
$4/15+2/5=?$
So what can you do when your denominators are unequal? You must make them equal by finding a common multiple (number they can both multiply evenly into) of their denominators.
In the case of $4/15+2/5$, a common multiple of the denominators 15 & 5 is 15.
When you find a common multiple of the denominators, you must multiply both the numerator and the denominator by the amount it took to achieve that number. Again, this keeps the fraction (the relationship between numerator and denominator) consistent. Think of it as the opposite of reducing a fraction.
To get to the common denominator of 15, $4/15$ must be multiplied by $1/1$ Why? Because 15*1=15.
$(4/15)(1/1)=4/15$. The fraction remains unchanged.
To get to the common denominator of 15, $2/5$ must be multiplied by $3/3$. Why? Because 5*3=15.
$(2/5)(3/5)=6/15$.
Now we can add them, as they have the same denominator.
$4/15+6/15=10/15$
We can further reduce $10/15$ into $2/3$ because both 10 and 15 are divisible by 5.
So our final answer is $2/3$.
Multiplying Fractions
Multiplying fractions is a bit simpler than adding or dividing fractions. There is no need to find a common denominator—you can just multiply the fractions straight across.
To multiply a fraction, first multiply the numerators. This product becomes your new numerator.
Next, multiply your two denominators. This product becomes your new denominator.
$1/4*2/3=(1*2)/(4*3)=2/12$
And again, we reduce our fraction. Both the numerator and the denominator are divisible by 2, so our final answer becomes:
$1/6$
Special note: you can speed up the multiplication and reduction process by finding a common factor of your cross multiples before you multiply.
$1/4*2/3$ => $1/2*1/3$. Why? Because both 4 and 2 are divisible by 2, we were able to reduce the cross multiples before we even began. This saved us time in reducing the final fraction at the end.
So now we can simply say:
$1/2*1/3=1/6$. No need to further reduce—our answer is complete.
Take note that reducing cross multiples can only be done when multiplying fractions, never while adding or subtracting them! It is also a completely optional step, so do not feel obligated to reduce your cross multiples—you can simply reduce your fraction at the end.
Dividing Fractions
In order to divide fractions, we must first take the reciprocal (the reversal) of one of the fractions. Afterwards, we simply multiply the two fractions together. Why do we do this? Because division is the opposite of multiplication, so we must reverse one of the fractions to turn it back into a multiplication question.
${2/3}÷{3/4}$ => $2/3*4/3$ (we took the reciprocal of $3/4$, which means we flipped the fraction upside down to become $4/3$)
$2/3*4/3=8/9$
But what happens if you need to divide a fraction by a whole number?
If a cake is cut into thirds and each third is cut into fourths, how many pieces of cake are there?
***
We start out with $1/3$ of a cake and we need to divide each third 4 more times.
Because 4 is a whole number, it can be written as $4/1$. This means that its reciprocal is $1/4$.
$1/3÷4$ => $1/3*1/4=1/12$
Our denominator (the whole) is 12. This means there will be 12 pieces total in the cake.
Decimal Points
Because fractions are pieces of a whole, you can also express fractions as either a decimal point or a percentage.
To convert a fraction into a decimal, simply divide the numerator by the denominator. (The / symbol also acts as a division sign.)
$4/5$ => 4/5 = 0.8
Sometimes it is easier to convert a fraction to a decimal in order to work through a problem. This can save you time and effort trying to figure out how to divide or multiply fractions.
***
As you can see, there are two ways to approach this problem—using fractions and using decimals. We’ll look at both ways.
If you were to use fractions, you would set up the problem as a fraction division problem.
$k=3/2$
So $j/k=j/{3/2}$
$j/{3/2}$ => $j*2/3$ (remember, we take the reciprocal when we divide)
So our full problem looks like this:
$2/3*j=32$
Now we must divide 32 by $2/3$ in order to bring it over to the other side and isolate j. This means we need to take the reciprocal yet again.
So ${32}/{2/3}$ => $32*3/2=96/2=48$
$j=48$
Now, for the final step, we must take $1/2$ of j. (Note: to "take $1/2$" is the same thing as multiplying by $1/2$.)
$48*{1/2}=48/2=24$
Our final answer is 24.
Alternatively, we could save ourselves the headache of using fractions and reciprocals and simply use decimals instead.
We know that $k=3/2$. Instead of keeping the fraction, let us convert it into a decimal.
$3÷2=1.5$
So $k=1.5$
$j/k=32$
$j/1.5=32$
When you multiply both sides by 1.5, you get:
$j=(32)(1.5)=48$
$j=48$
And ${1/2}j={1/2}(48)=24$
So again, our final answer is 24.
Percentages
After you convert your fraction to a decimal, you can also turn it into a percentage (if needed).
So 0.8 from can also be written as 80%, because 0.8*100=80.
A pie chart is a useful way of showing relative sizes of fractions and percentages. This shows just how large a fraction $7/10$ (or 70%) truly is.
Mixed Fractions
Sometimes you may be given a mixed fraction on the SAT. A mixed fraction is a combination of a whole number and a fraction.
For example, 7$3/4$ is a mixed fraction. We have a whole number, 7, and a fraction, $3/4$.
You can turn a mixed fraction into an ordinary fraction by multiplying the whole number by the denominator and then adding that product to the numerator. The final answer will be ${\the \new \numerator}/{\the \original \denominator}$.
7$3/4$
(7)(4)=28
28+3=31
So your final answer = $31/4$
You must convert mixed fractions into fractions in order to multiply, divide, add, or subtract them with other fractions.
In this problem, we began with 5 gallons of water and we ended with 2$1/3$. We must figure out how many gallons we used.
5−2
$5-2{1/3}$
First, let’s get our mixed fraction into a regular fraction.
2$1/3$ => ${[(2*3)+1]}/3={7/3}$
$5/1-7/3$
Now, we need to give each fraction the same denominator. We'll do this by converting $5/1$ into a new fraction with a denominator of 3.
$5/1*3/3=15/3$
Finally, we can find the difference between the amounts.
$15/3-7/3=8/3$
So we have used up $8/3$rds of the water.
Now let’s count how many times the pail was emptied to use up that $8/3$rds of the total water. If you count the dots, the pail was emptied 8 times (the first dot does not count as a time it was emptied—that is merely our starting point).
Because the same amount of water was removed each time, we must divide our emptied water by 8.
${8/3}÷{8/1}$ => $8/3*1/8$
We can now either reduce the cross-multiples (because this is a multiplication problem), which would give us:
$8/3*1/8$ => $1/3*1/1$
$1/3*1/1=1/3$
Or we can multiply through and then reduce afterwards:
$8/3*1/8=8/24$
$8/12=1/3$
Either way, our final answer is $1/3$; each trip removed $1/3$ of a gallon of water from the tank.
Now that we've broken down all there is to know about SAT fractions, let's take a look at their close cousin—the ratio.
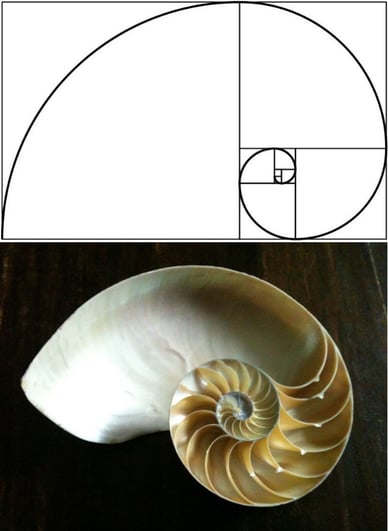This shape is called the "golden ratio" and has been studied for thousands of years. It has applications in geometry, nature, and architecture.
What are Ratios?
Ratios are used as a way to compare one thing to another (or multiple things to one another).
If Leslie has 5 white socks and 2 red socks, the white socks and the red socks have a ratio of 5 to 2.
Expressing Ratios
Ratios can be written in three different ways:
A to B
A:B
$A/B$
No matter which way you write them, these are all ratios comparing A to B.
Different Types of Ratios
Just as a fraction represents a part of something out of a whole (written as: ${\a \part}/{\the \whole}$), a ratio can be expressed as either:
apart:a different part
OR
apart:the whole
Because ratios compare values, they can either compare individual pieces to one another or an individual piece to the whole.
If Leslie has only 5 white socks and 2 red socks in a drawer, the ratio of white socks to all the socks in the drawer is 5 to 7. (Why 7? Because there are 5 white and 2 red socks, so together they make 5+2=7 socks total.)
Some of the many uses of ratios in action (in this case, the ratios are—a part: a different part).
Reducing Ratios
Just as fractions can be reduced, so too can ratios.
Kyle has a stamp collection. 45 of them have pictures of daisies and 30 of them have pictures of roses. What is the ratio of daisy stamps to rose stamps in his collection?
***
Right now, the ratio is $45:30$. But they have a common denominator of 15, so this ratio can be reduced.
$45/15=3$
$30/15=2$
So the stamps have a ratio of $3:2$
Increasing Ratios
Because you can reduce ratios, you can also do the opposite and increase them. In order to do so, you must multiply each piece of the ratio by the same amount (just as you had to divide by the same amount on each side to reduce the ratio).
So the ratio of 4:3 can also be
$4(2):3(2)=8:6$
$4(3):3(3)=12:9$
And so on.
Marbles are to be removed from a jar that contains 12 red marbles and 12 black marbles. What is the least number of marbles that could be removed so that the ratio of red marbles to black marbles left in the jar will be 4 to 3?
***
Right now, there are an equal amount of marbles, so the ratio is 12:12 (or 1:1)
We know that we have an end ratio of 4:3 that we want to achieve and that each side of the ratio has to be multiplied (or divided) by the same amount to keep the ratio consistent. We want to remove as few marbles as possible, so let us imagine that 4:3 is a reduced ratio.
That means we need to see how many total marbles the reduced ratio of 4:3 could possibly be. So both 4 and 3 have to be multiplied by the same amount to maintain their ratio and yet achieve a higher number of total marbles than just their 7 (4+3=7).
We can see that 12 is divisible by 4, so the red marbles could conceivably remain unchanged in order to get a new ratio of 4:3.
$12/4=3$
Because 4 can go evenly into 12, this will give us the fewest amount of marbles taken away. Because the 4 is multiplied 3 times to get 12, we know that both 4 and 3 must be multiplied by 3 to keep a new ratio of 4:3 consistent.
To find the new number of black marbles, we take 3*3=9.
The new amount of black marbles has to be 9. And because our red marbles remain the same (12), we must take only 3 marbles away from the total number of marbles (Why? Because 12 black marbles−3 black marbles=9 black marbles)
So our final answer is 3, we must take 3 black marbles away to get a new ratio of 4:3 of red marbles to black marbles.
Finding the Whole
If you are given a ratio comparing two parts (piece:anotherpiece), and you are told to find the whole amount, simply add all the pieces together.
It may help you to think of this like an algebra problem wherein each side of the ratio is a certain multiple of x. Because each side of the ratio must always be divided or multiplied by the same amount to keep the ratio consistent, we can think of each side as having the same variable attached to it.
For example, a ratio of 4:5 can be:
$4(1):5(1)=4:5$
$4(2):5(2)=8:10$
And so on, just as we did above.
But this means we could also represent 4:5 as:
$4x:5x$
Why? Because each side must change at the same rate. And in this case, our rate is $x$.
So if you were asked to find the total amount, you would add the pieces together.
$4x+5x=9x$. The total amount is 9x. In this case, we don’t have any more information, but we know that the total must be divisible by 9.
So let’s take a look at another problem.
Teyvon has a basket of eggs that he is going to sell. There are two different kinds of eggs in the basket—white and brown. The brown eggs are in a ratio of 2:3 to the white eggs. What is NOT a possible number of eggs that Teyvon can have in the basket?
A) 5
B 10
C) 12
D) 30
E) 60
***
In order to find out how many eggs he has total, we must add the two pieces together.
So 2+3=5
This means that the total number of eggs in the basket has to either be 5 or any multiple of 5. Why? Because 2:3 is the most reduced form of the ratio of eggs in the basket. This means he could have:
$2(2):3(2)=4:6$ eggs in the basket (10 eggs total)
$2(3):3(3)=6:9$ eggs in the basket (15 eggs total)
And so forth. We don’t know exactly how many eggs he has, but we know that it must be a multiple of 5.
This means our answer is C, 12. There is no possible way that he can have 12 eggs in the basket.
Now that we are armed with knowledge of fractions and ratios, we must follow the right steps to solve our problems.
How to Solve Fraction, Ratio, and Rational Number Questions
Now that we have discussed how fractions and ratios work indivisually, let's look at how you'll see them on the test. When you are presented with a fraction or ratio problem, take note of these steps to find your solution:
#1: Identify whether the problem involves fractions or ratios
A fraction will involve the comparison of a $\piece/\whole$.
A ratio will almost always involve the comparison of a piece:piece (or, very rarely, a piece:whole).
You can tell when the problem is ratio specific as the question text will do one of three things:
- Use the : symbol,
- Use the phrase "___ to ___”
- Explicitly use the word "ratio” in the text.
If the questions wants you to give an answer as a ratio comparing two pieces, make sure you don’t confuse it with a fraction comparing a piece to the whole!
#2: If a ratio question asks you to change or identify values, first find the sum of your pieces
In order to determine your total amount (or the non-reduced amount of your individual pieces), you must add all the parts of your ratio together. This sum will either be your complete whole or will be a factor of your whole, if your ratio has been reduced.
A total of 120,000 votes were cast for 2 opposing candidates, Garcia and Pérez. If Garcia won by a ratio of 5 to 3, what was the number of votes cast for Pérez?
(A) 15,000
(B) 30,000
(C) 45,000
D) 75,000
(E) 80,000
***
As you can see, our ratio of 5 to 3 has been greatly reduced (neither of those numbers is in the tens of thousands). We know that there are a total of 120,000 votes, so we need to determine the number of votes for each candidate.
Let’s first add our ratio pieces together.
5:3 => 5+3=8
Because 8 is much (much) smaller than 120,000, we know that 8 is not our whole. But 8 is the factor of our whole.
${120,000}/8=15,000$
So if we think of 15,000 as one component (a replacement for our variable, $x$), and Garcia and Pérez have a ratio of 5 components to 3 components, then we can find the total number of votes per candidate.
G:P=5:3 => $5x:3x$
5*15,000=75,000
3*15,000=45,000
So Garcia earned 75,000 votes and Pérez earned 45,000 votes. (You can even confirm that this must be the correct number of votes each by making sure they add up to 120,000. 75,000+45,000=120,000. Success!)
So our final answer is C, Pérez earned 45,000 votes.
#3: When in doubt, try to use decimals
Decimals can make it much easier to work out problems (as opposed to using fractions). So do not be afraid to convert your fractions into decimals to make life easier.
#4: Remember your special fractions
Always remember that a number over 1 is the same thing as the original number, and that a number over itself = 1.
If $h$ and $k$ are positive numbers and $h+k=7$ then ${7-k}/h=$
(A) 1
(B) 0
(C) -1
(D) $h$
(E) $k-1$
***
Here we have two equations:
$h+k=7$
and
${7-k}/h$
So let us manipulate the first.
$h+k=7$ can be re-written as:
$h=7−k$ (Why? We simply subtracted $k$ from either side)
So now we can replace the $(7−k)$ from the second equation with $h$, as the two terms are equal.
This leaves us with:
$h/h$
And we know that any number over itself = 1.
So our final answer is A, 1.
Test Your Knowledge
#1:
Flour, water, and salt are mixed by weight in the ratio of 5:4:1, respectively, to produce a certain type of dough. In order to make 5 pounds of this dough, what weight of salt, in pounds, is required?
(A) $1/4$
(B) $1/2$
(C) $3/4$
(D) 1
(E) 2
#2:
#3: Which of the following answer choices presents the fractions $5/4$, $4/3$, $19/17$, $13/12$, and $7/6$ in order from least to greatest?
(A) $19/17$, $7/6$, $13/12$, $4/3$, $7/6$, $5/4$
(B) $4/3$, $5/4$, $7/6$, $19/17$, $13/12$
(C) $13/12$, $7/6$, $19/17$, $5/4$, $4/3$
(D) $19/17$, $13/12$, $5/4$, $7/6$, $4/3$
(E) $13/12$, $19/17$, $7/6$, $5/4$, $4/3$
Answers: B, D, E
Answer Explanations:
#1: This question is a perfect example of when to find the whole of the pieces of the ratio. Flour, water, and salt are in a ratio of 5:4:1, which means that the whole is:
$5x+4x+1x=10x$
So $10x$ is our whole.
We want 5 pounds of the recipe, so we must convert $10x$ to 5.
$10x=5$
$x=1/2$
Our variable is $1/2$
.
Now, we are looking for the amount of salt to use when we started out with $1x$. So let us replace our $x$ with the value we found for it.
$1x$
$1(1/2)$
$1/2$
This means we need $1/2$ a pound of salt to make 5 pounds of the mixture.
Our final answer is B, $1/2#.
#2: For this question, we must find a non-zero integer for t in which $x+{1/x}=t$, where $x$ is also an integer.
We know, based on our special fractions, that the only possible way to get a whole number in fraction form is to have our demoninator equal 1 or -1. This means that x cannot possibly be anything other than 1 or negative 1.
(Why? If x were anything else but 1, we would end up with a mixed fraction. For example, if x=2, then we would have:
$2+{1/2}$. If $x=3$, we would have:
$3+{1/3}. And so on. The only way to get an integer value for $t$ is when $x=1$.)
So let us try replacing our $x$ value with 1.
$x+{1/x}=t$
$1+{1/1}=2$
$t=2$
Well, $t$ could possibly equal 2, but this is not one of our answer choices. So now let us replace $x$ with -1 instead.
$x+{1/x}=t$
$-1+{1/-1}=-2$
t=−2
Success! We have found a value for $t$ that matches one of our answer choices.
Our final answer is D, $t=−2$
#3: For a problem like this (one that has you order fractions by size), it is usually a good idea to break out the decimals. But we will go through how to solve it using both methods of fractions and decimals.
Solving with decimals:
To solve with decimals, simply divide each numerator by its denominator to get the decimal. Then, order them in ascending order (as we are told).
$5/4=1.25$
$4/3=1.333$
$19/17=1.12$
$13/12=1.08$
$7/6=1.16$
We can see here that the order from least to greatest is:
1.08, 1.12, 1.16, 1.25, 1.33
Which, converted back to their fraction form is:
$13/12$, $19/17$, $7/6$, $5/4$, $4/3$
So our final answer is E.
Alternatively, we can solve using fractions.
Solve using fractions:
Let us find a common denominator between all the numerators. A quick way to do this is by multiplying the two largest numerators together. (It may not be the least common denominator, but it'll do for our purposes.)
$17*12=204$
Now let's make sure that the other denominators can go evenly into 204 as well.
$204/6=34$
$204/4=51$
$204/3=68$
Perfect! Now let us convert all of our fractions.
$5/4={5(51)}/{4(51)}=255/204$
$4/3={4(68)}/{3(68)}=272/204$
$19/17={19(12)}/{17(12)}=228/204$
$13/12={13(17)}/{12(17)}=221/204$
$7/6={7(34)}/{6(34)}$
Now that they all share a common denominator, we can compare and order their numerators. So, in ascending order, they would be:
$221/204$, $228/204$, $238/204$, $255/204$, $272/204$
Which, when converted back to their original form, is:
$13/12$, $19/17$, $7/6$, $5/4$, $4/3$
So again, our final answer is E.
I think a nap is in order—don't you?
Take-Aways
Fractions and ratios may look tricky, but they are merely ways to represent the relationships between pieces of a whole and the whole itself. Once you know what they mean and how they can be manipulated, you’ll find that you can tackle most any fraction or ratio problem the SAT can throw at you.
But always remember—though ratios and fractions are related, do not get them mixed up on the SAT! The vast majority of the time, the ratios they give you will compare parts to parts and the fractions will compare parts to the whole. It can be easy to make a mistake during the test, so don’t let yourself lose a point due to careless error.
What’s Next?
You've conquered fractions and you've decimated ratios and now you're eager for more, right? Well look no further! We have guides aplenty for the many math topics covered on the SAT, including probability, integers, and solid geometry.
Feel like you're running out of time on the SAT? Check out our article on how to finish your math sections before time's up.
Don't know what score to aim for? Make sure you have a good grasp of what kind of score would best suit your goals and current skill level, and how to improve it from there.
Angling to get an 800 on SAT Math? Look to our guide on how to get a perfect score, written by a perfect SAT scorer.
