
Worried about exponents or coordinate geometry on the SAT? Never fear, this guide is here!
I'll explain everything you need to know about SAT Math's trickiest subject area: Passport to Advanced Math. This topic tests all the algebra skills you must have firmly in place before you move into the study of more complex math, including systems of equations, polynomials, and exponents. Of course, the questions are presented in a uniqely SAT way, so I'll walk you through exactly what you can expect from this subsection of SAT Math.
Basic Data: Passport to Advanced Math
There are 16 Passport to Advanced Math questions on the test (out of 58 total math questions). These questions will not be explicitly identified—there's no label or anything marking these questions as members of this category—but you will receive a subscore (on a scale of 1 to 15) indicating how well you did on this material.
You will see this type of question in both the calculator and no-calculator sections. There will also be both multiple choice questions and grid-in questions covering these topics.
Passport to Advanced Math Concepts
Below are the major skills tested by Passport to Advanced Math questions.

Pay attention, now!
Understanding Equation Structure
The College Board wants to know that you understand how expressions, equations, and the like are structured. Also, the College Board will call upon you to demonstrate a real comprehension of why they're structured that way—and how they work as a result.

For a question like this, you need to put both sides of the equation in the same form. So we'll start by FOILing the left side of the equation:
$$abx^2+7ax+2bx+14=15x^2+cx+14$$
By comparing the two sides of the equation we can draw two conclusions:
$$ab=15$$
$$7a+2b=c$$
Now we can use the following system of equations to determine the possible values for $a$ and $b$:
$$a+b=8$$
$$ab=15$$
Therefore, $a=3$ and $b=5$, or $a=5$ and $b=3$.
Finally, we plug both of those possible sets of values into the equation $7a+2b=c$ and solve for $c$, which gives us $c=7(3)+2(5)=31$ or $c=7(5)+2(3)=41$.
Thus, (D) is the correct answer.
Modeling Data
You'll have to demonstrate the ability to build your own model of a given situation or context by writing an expression or equation to fit it.
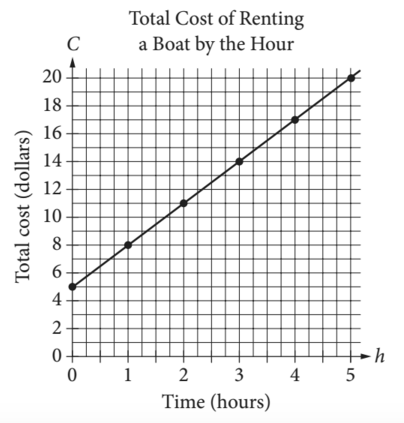

Here, the testmakers are asking us to recognize that $C$ is a function of $h$. We're looking at a variation on $y=mx+b$ where $C$ is on the y-axis and $h$ is on the x-axis. In order to find the correct equation for the line, we need to determine the values of constants $m$ (slope) and $b$ (y-intercept).
We can look at the graph and immediately see that the y-intercept is 5, but that only allows us to rule out answers A and D. We need to find the slope as well.
The equation for the slope of a line is $m=(y_2-y_1)/(x_2-x_1)$
Let's choose points $(1,8)$ and $(2,11)$ from the graph and plug these values into the slope equation:
$$m=(11-8)/(2-1)=(3/1)$$
Given a slope of 3 and y-intercept of 5, we know the correct equation is $C=3h+5$, so the answer is (C).

Mathematical modeling will, unfortunately, not get you on the front page of Vogue.
Manipulating Equations
This skill is very important to have mastered, as it will be useful in a large number of problems.
It's all about where you can rearrange and rewrite expressions and equations.

This question is pretty straightforward in asking you to rearrange the original formula. The math needed to do so, however, looks pretty nasty, by a glance over the answer choices. Let's take a look.
Really, all we're doing is dividing both sides by the big nasty part, which is to say we're dividing by:

To do that, we can multiply both sides by the reciprocal, which is:
$${(1+r/1200)^N-1}/{(r/1200)(1+r/1200)^N}$$
So, we have:
$$m{(1+r/1200)^N-1}/{(r/1200)(1+r/1200)^N}={(r/1200)(1+r/1200)^N}/{(1+r/1200)^N-1}{(1+r/1200)^N-1}/{(r/1200)(1+r/1200)^N}P$$
The two fractions on the right cancel each other out and this simplifies to:
$$m{(1+r/1200)^N-1}/{(r/1200)(1+r/1200)^N}=P$$
The answer is (B).

Math is one place where manipulation is not a malicious or fraudulent activity.
Simplification
This aspect is all about turning down the noise within an expression or equation by canceling out useless terms. In other words, the testmakers are likely to throw a whole lot of impenetrable garbage at you and wait for you to rearrange it so it makes human sense.

This question is relatively straightforward: it just looks like a handful. It's all a matter of lining up like terms and combining them; careful of the signs. First, we distribute the negative to the terms in the second set of parentheses:
$$x^2y-3y^2+5xy^2+x^2y-3xy^2+3y^2$$
Then we combine like terms:
$$(x^2y+x^2y)+(-3y^2+3y^2)+(5xy^2-3xy^2)=2x^2y+2xy^2$$
Thus, (C) is the correct answer.
Specific Topics in Math
Here, we'll talk less about the broad scope of skills you'll need and more about specifics topics you have to be familiar with.
Systems of Equations
You need to be able to solve a system of equations in two variables where one is linear and one is quadratic (or otherwise nonlinear). Often, you will need to identify extraneous solutions—so don't forget to double-check the answers you find to make sure they work.

There's a lot going on with this question, so let's start by simplifying the first equation.
$$x^a^2/x^b^2=x^16$$
$$x^(a^2-b^2)=x^16$$
Since we know $x=x$, we can infer the following equation:
$$a^2-b^2=16$$
$$(a+b)(a−b)=16$$
We know $a+b=2$, so we can plug that in and solve for $a-b$:
$$2(a-b)=16$$
$$a-b=16/2=8$$
 The equations on the SAT tend to be more complicated than this one, though.
The equations on the SAT tend to be more complicated than this one, though.
Polynomials
You need to be able to add, subtract, multiply, and even occasionally divide polynomials.
With polynomial division comes rational equations. You've got to be able to clear variables out of the denominator in rational expressions.

Clearly the issue here is simplifying that rather intimidating denominator. Let's try multiplying the whole thing by ${(x+2)(x+3)}/{(x+2)(x+3)}$.
$$1/{1/(x+2)+1/(x+3)}{(x+2)(x+3)}/{(x+2)(x+3)}$$
$${(x+2)(x+3)}/[{(x+2)(x+3)}/(x+2)+{(x+2)(x+3)}/(x+3)]$$
$${(x+2)(x+3)}/{(x+3)+(x+2)}$$
$$(x^2+5x+6)/(2x+5)$$
You'll recognize that as answer (B).
The "polynomial" heading also includes your friendly neighborhood quadratic functions and equations. You need to be able to devise your own quadratic equation from the context of a word problem.
Exponential Functions, Equations, Expressions, and Radicals
You need an understanding of exponential growth and decay. You also need a solid comprehension of how roots and powers work.

This question looks vaguely impossible, but the trick is just realizing that $8=2^3$. Once we know that we can rewrite the expression:
$(2^3^x)/2^y=2^(3x-y)$
Per the question, we know that $3x-y=12$, so we can plug that value into the expression above to get $2^12$ or (A).

Oh, the fun we can have with exponents!
Algebraic and Graphical Representations of Functions
Here are some terms you should understand, both as they apply to functions and as they apply to graphs. What do they mean in each case?
- x-intercepts
- y-intercepts
- domain
- range
- maximum
- minimum
- increasing
- decreasing
- end behavior
- asymptotes
- symmetry
You'll also need to understand transformations. You should understand what happens, algebraically and graphically, when $f(x)$ changes to $f(x)+a$ or $f(x+a)$. What's the difference? Adding a outside of the parentheses moves the function up or down, graphically, and increases or decreases the overall values being spit out, algebraically. Adding a inside of the parentheses moves the function side to side, graphically, and shift the output the corresponds to the formal input, algebraically.
Analyzing More Complex Equations in Context
Sometimes you need to combine your "mathematical" knowledge with a plain old sense of logic. Don't be afraid to plug numbers in and watch what's going on in that alphabet soup when you try some actual values. Take everything step by step.
Tips for Passport to Advanced Math
The Passport to Advanced Math questions can be tricky, but the following tips can help you approach them with confidence!
#1: Use multiple choice answers to your advantage. Always keep an eye out for what may be plugged in, tried out, or worked backwards from. One of the answers listed has to be the right one, so toy around with those four options until it all falls into place. Be sure to read our articles on plugging in answers and plugging in other useful numbers. Also, don't forget the process of elimination! If two answers are definitely bad and two might be okay, at least you're now guessing with a 50-50 chance of success—and that's not too bad!
#2: Remember that squaring an expression isn't something you can really undo. There are so many problems where it's tempting—and often best—to square an expression, but remember there are caveats if you do. You may end up with extraneous solutions or some other such nonsense. Squaring also wipes out any negatives that are present. Taking a square root messes with the signs in a different way: you're going to have a positive case and a negative case, and that may not be appropriate.
#3: Make sure you understand how the laws of exponents and how powers and radicals all relate. These laws can be pesky to memorize, but they're crucial to know. Exponents show up a lot on the test, and not knowing how to manipulate them is just a way of robbing yourself of all of those points.

There he is! The dreaded points-robber!
Closing Words
There are a few fundamental skills that are essential to doing well on Passport to Advanced Math questions on the SAT.
A lot of it comes down to knowing the different forms that an expression or equation can take—and understanding what they al mean. Basically, get comfortable with equivalences, and with mathematical operations used on terms more complex than plain old constants, because you'll be seeing plenty of them.
Another thing that this type of question tests is your ability to recognize information—and I mean this in the pure sense of noticing that a certain term can be factored out, that it would be convenient to rewrite an equation with a different system of organizations, or that if I shoved most of the terms in an equation to the opposite side of the equals sign than I would be left with the difference of squares on one side. This awareness is, unfortunately, the hardest part to teach—and one of the most important to practice.
Remember to stay calm—and breathe. Use your time wisely: if a problem looks totally overwhelming, skip it. Save it for the end, and however much time (if any) you have left over.
If you sense that you're truly stuck, guessing is not the end of the world—it's better than leaving a question blank. There's no guessing penalty, so you won't lose points for a wrong answer.
Before you throw in the towel, though, and time permitting, take a few minutes to fiddle around with the problem, trying out some different strategies. Try anything that comes to you! Work backwards from the answer choices, trying them out and plugging things in.
What's Next?
Now, if I gave the impression that any of these skills are impossible to learn, I apologize. Certain skills are harder to pick up, but we've got resources that should give you a leg up.
We've got explanatory articles that cover just about anything you could ever want to know about SAT Math.
Now, anxiety results from anticipating the unknown, so make the worst of the possible worst on SAT Math a little less mysterious by trying out some extra tough problems.
And, just in case, learn how to do your very best guessing on SAT Math.











