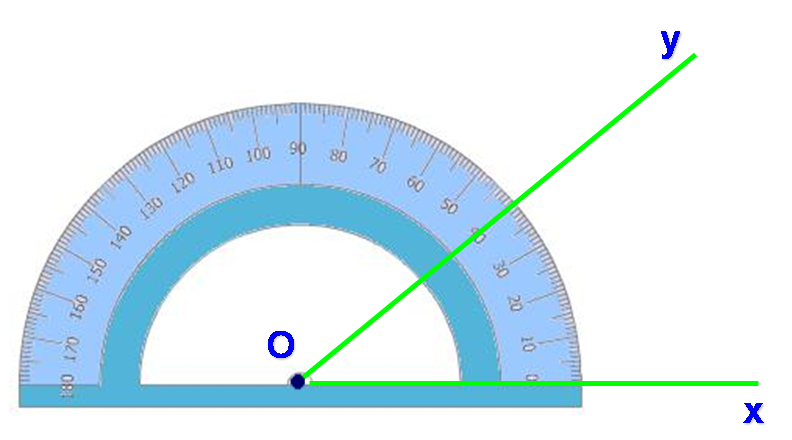
There are several math topics that act as foundations for understanding ACT Math, even though there are not many questions specifically dedicated to the topic. This is most certainly the case for line and angle problems. Though it is rare to see a pure line and angle problem (without the addition of other geometric shapes), you’ll need to know just how lines and angles work and how to solve for all your missing measures before you can take on those more complex problems.
This will be your complete guide to lines and angles on the ACT—what they are, how you’ll see them on the test, and how to solve these types of questions to maximize your points on test day.
Properties of Lines and Angles
Before we get into how lines and angles function, let’s define our terms.
A line is a completely straight marker, meaning it has no curvature. It can either have termination points (and will be called a “line segment”) or go on infinitely.
Its degree measure is always 180°.
Parallel lines are two or more lines that are a set distance apart (equidistant) and never meet. They travel in the same direction continuously.
Perpendicular lines meet each other at 90 degree angles.
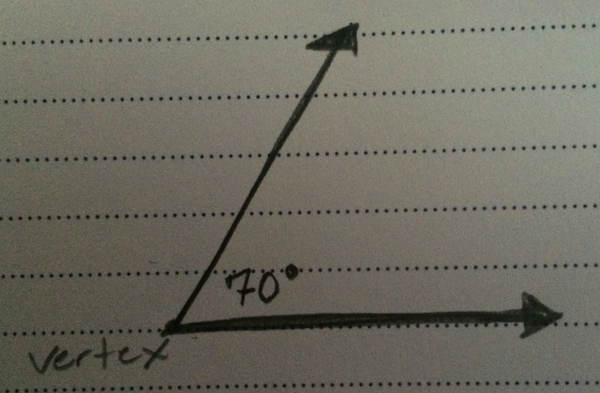
An angle is the meeting of two lines. The measure of how they meet is expressed in degrees, and the point at which they intersect is called the angle’s “vertex.”
Line and Angle Equalities
Most of what you’ll need to know about lines and angles on the ACT is how to identify when and how they will be equal or supplementary to one another.
Equal angles (or lines) are angles (or lines) that have the same measurement.
Supplementary angles are angles that add up to 180 degrees.
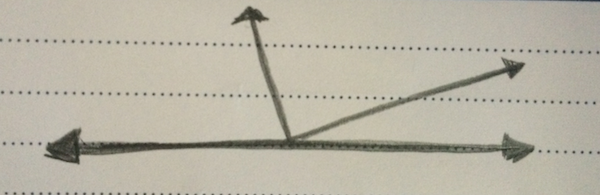
Because all these angles form a straight line and a straight line equals 180 degrees, the three angles are supplementary.
Opposite Angles
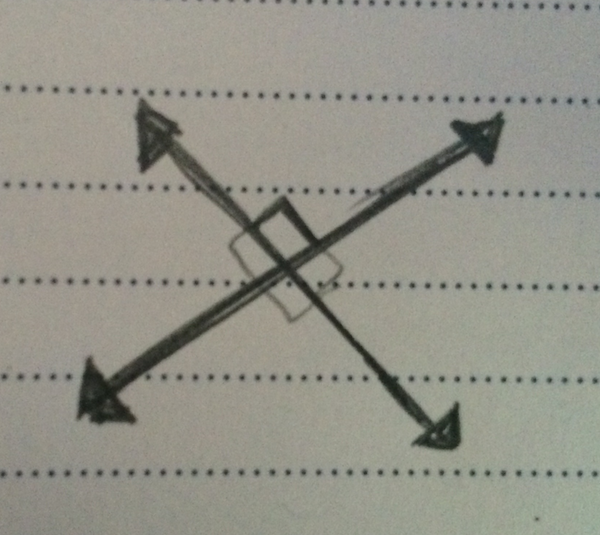
When two (or more) lines intersect, they form a series of opposite angles. Angles that are exactly opposite will always be equal to one another.
Both sets of opposite angles will be equal.
Opposite Interior Angles
When there are two parallel lines that are crossed by another line (called a transversal), the angles on alternate interiors will be equal to one another. And the angles that are on the same side of the transversal line and the same side of their respective parallel lines will also be equal.&
That may be difficult to picture, so let’s look at a diagram:
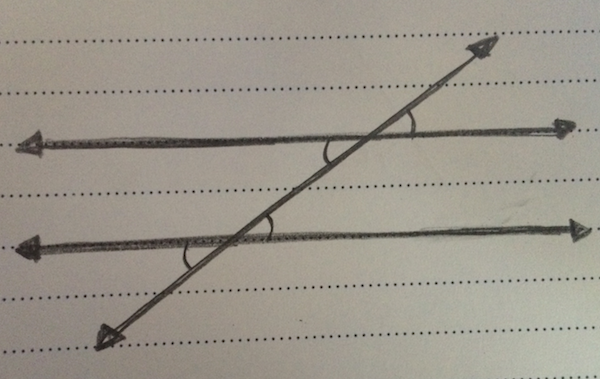
The marked angles are all congruent (equal) and the unmarked angles are all congruent.
(Note: when you are told that two lines are parallel on ACT Math, the problem will almost always involve opposite interior angles in some way.)
Now let’s look at an opposite interior angle ACT problem.
Here, the test has made it slightly tricky by asking you for supplementary angles instead of equal ones. But the principle remains the same—we must identify angle measurements/equalities by using opposite interior angle equalities.
We can see straight away that $x$ lies on a straight line with both 1 and 2, so angles 1 and 2 will be supplementary with $x$.
We can also see that angles 1 and 10 are opposite interior angles and so will be equal to one another. And angle 9 is opposite angle 10 and thus will also be equal.
This means that angle $1 = 2 = 9 = 10$ and all are supplementary to $x$.
Finally, we can ignore the angles 4, 5, 6, 7 and 12, 13, 14, 15. Why? Because lines $c$ and $d$ are not parallel and so do not have opposite interior angle equalities.
This means that $x$ is only supplementary to angles 1, 2, 9, 10.
Our final answer is H.
Equal lines and equal angles can be quite disorienting in the right hands.
Typical Line and Angle Problems
Almost every line and angle problem on the ACT is given to you as a diagram problem. You will be presented with a series of givens and then told to find a missing value of some kind. Almost always, this requires multiple steps and the use of multiple pieces of line/angle knowledge.
The other notable feature of lines and angle problems on the ACT is that you will be given a “pure” line and angle problem very rarely. Most of them involve other geometric shapes in some way, most commonly triangles.
The good news is that you will generally not need to know more than the fact that all the interior angles in a triangle add up to 180 degrees, but check out our guide to ACT triangles if you are unfamiliar with or unused to working with triangles.
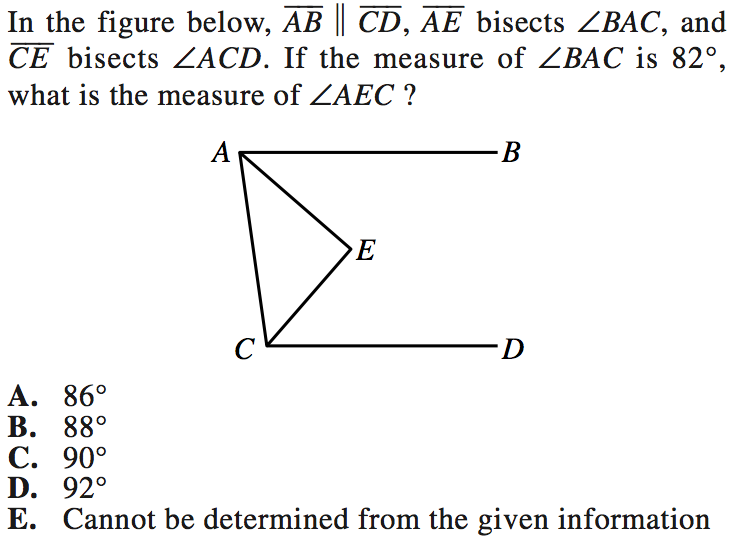
Now, we are told that two lines are parallel, so there’s a good chance we’ll need to use our opposite interior angle knowledge. With that in mind, let us expand the drawing we are given so that we can see our opposite interior angles more clearly.
Using our opposite interior angles, we know that angle BAC is 82, which means that angle ACX must also be 82 degrees.
We can also see that angles ACX and ACD make a straight line. Their sum must therefore be 180 degrees.
$ACX + ACD = 180$
$82 + ACD = 180$
$ACD = 98$
We are also told that lines AE and CE are bisectors, which means they cut their respective angles exactly in half.
This means that angle EAC = $82/2 = 41$
And angle ECA = $98/2 = 49$
Now, we also know that a the interior angles of a triangle add up to 180 degrees, so we are able to find our angle measure AEC by:
$AEC + EAC + ECA = 180$
$AEC + 41 + 49 = 180$
$AEC + 90 = 180$
$AEC = 90$
Our final answer is C, angle AEC is 90 degrees.
As we said before, this question is representative of most line and angle problems you’ll see on the test. Based on your givens, you must use your knowledge of opposite interior angles (opposite interiors are equal) and your knowledge of the degree measure of a line (a line is 180 degrees) in order to put together all the clues and solve your problem.
And yet, in addition to understanding the properties of lines and angles by themselves, you must also understand the basics of triangles. Because many ACT problems that involve lines and angles also use triangles, your knowledge of lines and angles should definitely be supplemented with triangle study. So don’t forget to brush up on your ACT triangles!
Now let's check out our angle tips and tricks.
Tips for Solving a Line and/or Angle Problem
Most of the time, you must solve a line and angle question piece by piece in order to unlock the final solution. This means you must be careful and vigilant that you keep not only your facts and equalities straight, but your variables as well.
As you go through this process, keep in mind these three tips:
Tip 1: Write in your givens
If you are given a diagram in which your givens are NOT written in, then write them in yourself! Sometimes, seeing the numbers on the page can make all the difference in the world between a difficult problem and an easy one.
You’ll also be far less likely to mix up your numbers and variables if you keep your work on the page instead of in your head.
Tip 2: Work from your givens to find the next puzzle piece
Sometimes, it can be tricky to know where or when or in what order to work through a problem. Take a moment to find what you can before you worry about how to go forward.
If you have opposite angles, write in the measure of the angle opposite your given. If you have angles that make a straight line, find the value of the missing variable. Immediately find the missing pieces that you can, and that bounty of information will often lead you straight to your solution.
Tip 3: If necessary, use plugging in answers or plugging in numbers
If you find yourself stuck (or there is literally no other way to solve the problem), then whip out your PIA or PIN knowledge. Sometimes the process can be slower than a straight solve, but these strategies will almost always get you where you need to go and so can be worth the extra seconds.
Ready to put your knowledge to the test?
Test Your Knowledge
1.
2.
3.
4.
Answers: C, J, B, B
Answer Explanations:
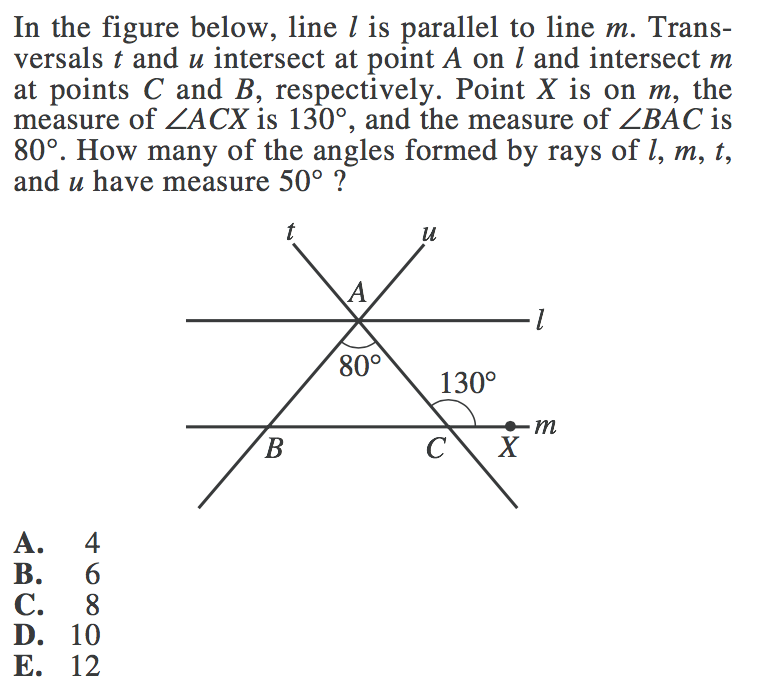
1. This problem requires multiple steps, so definitely write in your angle measurements as you find them. In order to find out how many angles measure 50 degrees, we must find the measures of all our angles, so let's go through the process.
To begin with, we can see that the 130 degree angle lies on a straight line, so its supplementary angle will be:
$180 - 130 = 50$ degrees.
Now, we also know that opposite angles are equal, so the angle opposite 50 degrees must also be 50 degrees.
We also know that a triangle adds up to be 180 degrees and that our figure in the center is a triangle. So:
$180 - 80 - 50 = 50$ degrees.
This means that the missing value in our triangle is also 50 degrees.
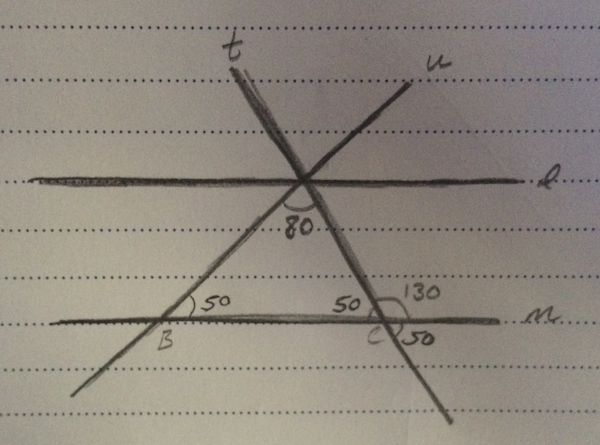
Again, we know that opposite angles equal one another, so the angle opposite this 50 degrees will also be 50 degrees.
Based on opposite interior angle equalities, the full angle at the opposite 130 degrees will also be 130 degrees.
Because the full angle is 130 degrees and part of it is made up of an 80 degree angle, which means that we can find the other angle by saying:
$130 - 80 = 50$
And again, the angle opposite this 50 degree angle will also be 50 degrees.
We can also see that the 80 degree angle, plus the 50 degree angle, plus one of the unmarked angles will equal 180 degrees, since they make up a straight line. So we can find the unmarked angle by saying:
$180 - 80 - 50 = 50$
Finally, we can use opposite angle equalities to find the last unmarked angle.
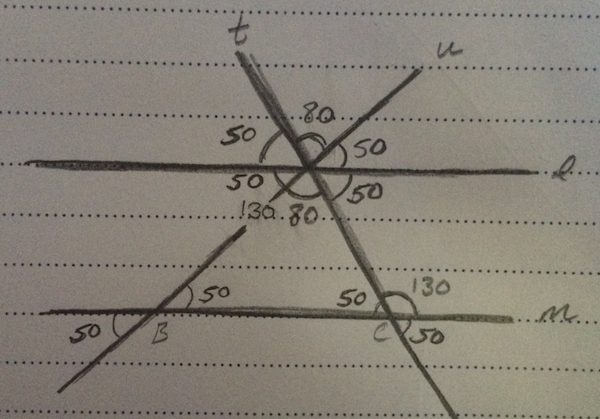
We have found all our angle equalities, so all that's left is to count how many angles are equal to 50 degrees.
There are a total of 8, 50 degree angles.
Our final answer is C, 8.
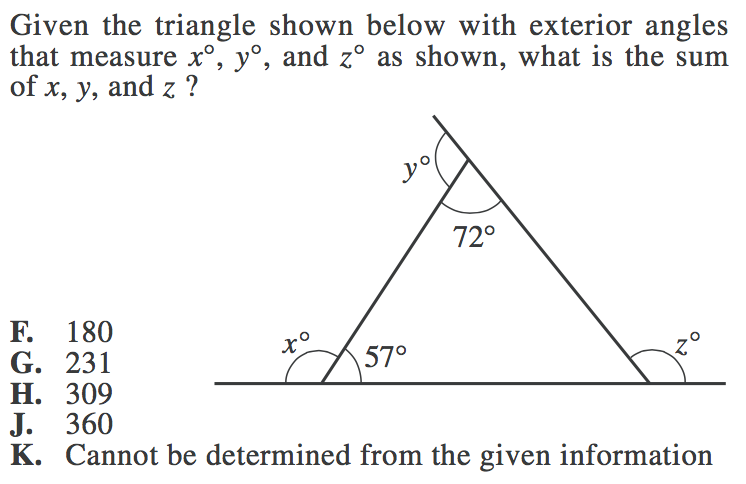
2. For this question, we must use our knowledge that both straight lines and the sum of the interior angles in a triangle equal 180 degrees.
First, let us find the measure of angle $y$. Angle $y$ makes a straight line with the 72 degree angle, so:
$y + 72 = 180$
$y = 108$
Now, we can use the same process to find angle $x$, which forms a straight line with the 57 degree angle.
$x + 57 = 180$
$x = 123$
Now, let us find angle $z$ by first finding the third, unknown, angle in the triangle (which we will call angle $a$).
The interior angles in a triangle add up to 180 degrees, so:
$a + 57 + 72 = 180$
$a + 129 = 180$
$a = 51$
Now, let’s use that angle to find $z$. The two angles make a straight line, so their sum will be 180.
$a + z = 180$
$51 + z = 180$
$z = 129$
(Note: you may notice that the sum of the two non-adjacent interior angles of the triangle is equal to the exterior angle. This is not a coincidence and is in fact one of the many rules of triangles. But don’t worry about having to memorize this rule—you can always find the exterior angles using the properties of straight lines just how we did!)
Now, we must find the sum of angles $x, y,$ and $z$, so let’s add our values together.
$108 + 123 + 129$
$360$
Our final answer is J, 360.
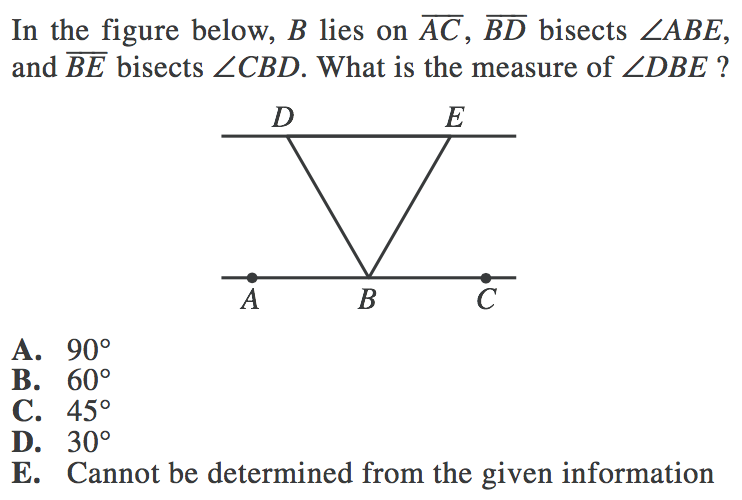
3. Here, we are dealing with several bisecting angles. This means that the angles are cut exactly in half.
This means that angle ABD = DBE and angle DBE = EBC.
And because DBE is equal to both ABD and EBC, it means that angles ABD and EBC are also equal.
This means that we have three equal angles, all making one line. And we know a line equals 180 degrees, so:
$x + x + x = 180$
$3x = 180$
$x = 60$
Each angle measure is 60 degrees, which means that angle DBE is 60 degrees.
Our final answer is B, 60 degrees.
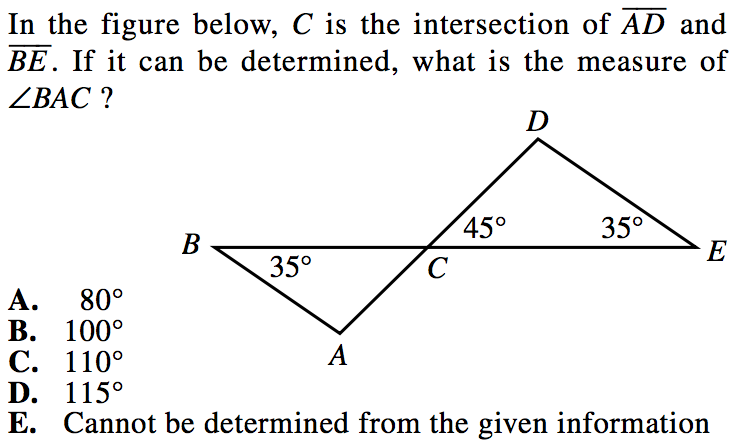
4. We can see that angle BAC is part of a triangle. And we know that we need two angle measures of a triangle in order to determine the third.
But we can also see that the 45 degree angle is opposite one of our unknown interior triangle angles. Because opposite angles are equal, this means that our second unknown interior angle of the triangle is 45 degrees.
We now have two angle measures of the triangle, so let us find the measure of BAC.
$BAC + 35 + 45 = 180$
$BAC + 80 = 180$
$BAC = 100$
Measure BAC is 100 degrees.
Our final answer is B, 100 degrees.
These problems require multiple steps, but the process is often simpler than it looks. So don't tire yourself out prematurely.
The Take-Aways
The trickiest aspect about line and angles questions is the fact that they require multiple steps and several different numbers and measurements. It can be easy to mix-up your solutions and your work due to careless error, so make sure you take steps to avoid doing so.
Remember your equalities, keep your work organized, and do your best to avoid careless errors. Once you’ve locked down lines and angles, you will be well equipped to take on the more and more complex geometry problems the ACT will throw at you over the course of the test.
What’s Next?
Now that you've learned all about your lines and angles, make sure you're up to speed on the rest of your must-know math topics and formulas for the ACT. Look to our ACT Math tag for all of our guides to ACT Math, including ratios, solid geometry, and more.
Studying last minute? Check out our tips for making your time count before test day.
Running out of time on the ACT math section? Make sure you review how to buy yourself extra time as you go through your test.
Looking to get a perfect score? Perfection is far from unobtainable, so check out our article on how to get a 36 on ACT Math, written by a perfect scorer.
