If you thought the ACT was a big fan of circles, then brace yourself for its absolutely shameless love of triangles. In one breath, you may be expected to find the various dimensions of an obtuse triangle, and the next, an isosceles right triangle. ACT triangle problems will be as numerous as they are varied, so make sure you familiarize yourself with all the different types before test day.
This will be your complete guide to ACT triangles--the types of triangles that will show up on the ACT, the formulas you’ll need to know to solve them, and the strategies you’ll need to apply when approaching a triangle question. We’ll also break down real ACT math problems and give you the walk-throughs on how to most efficiently and effectively tackle any and all triangle problems you come up against.
What Are Triangles?
Before we go through how to solve a triangle problem, let’s discuss the basics. A triangle is a flat figure made up of three straight lines that connect together at three angles. The sum of these angles is 180°.
Each of the three sides of a triangle is called a “leg” of the triangle, and the largest (longest) leg is called the “hypotenuse.” The angle opposite the hypotenuse will always be the largest of the three angles.
The sum of any two legs of a triangle must always be greater than the measure of the third side. Why? Because when the sum of two lines is smaller than the measure a third line, they cannot all connect to form a triangle.
Triangles that have legs which sum only slightly more than the hypotenuse are quite long and skinny, but they still make the “bump” of a triangle because they combine to be longer than the third side.
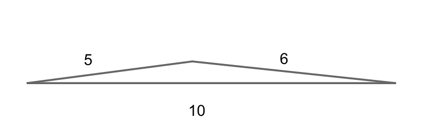
But if the legs are too short, they will never meet, no matter how shallow the angle.
And if the lines are the exact length of the hypotenuse, then they will flatten to a perfectly straight line, overlapping the hypotenuse precisely.
Let's look at an example ACT problem of this kind:
A triangle has side lengths of 6 inches and 9 inches. If the third side is an integer, what is the least possible perimeter, in inches, of the triangle?
-
4
-
15
-
18
-
19
-
29
We know, based on our rules for the side lengths of triangles, that the sum of two sides must be greater than the third. Because we are trying to find the smallest perimeter, we must find our missing side by taking the difference of our two leg lengths:
$9 - 6 = 3$
Considering the sum of two legs must be greater than the third side, our missing side must be greater than 3. (Why? Because $6 + 3 = 9$ and we need the sum to be larger than 9.)
If our missing side is an integer value (which we are told is true), and we are trying to find the minimum perimeter value, then our missing side must be the smallest integer greater than 3.
Which means that our missing side is 4.
To find our perimeter, then, we must add all our sides together:
$4 + 6 + 9 = 19$
Our final answer is D, 19.
(Note: always pay attention to the exact question you’re being asked and don’t get tricked by bait answers! If you were going too quickly through the test, you might have been tempted to select answer choice A, 4, which was the value of the missing side length. But, since we were asked to find the perimeter, this would have been the wrong answer.)
Ready to enter the realm of special triangles (and become insanely awesome)?
Special Triangles
There are several different kinds of special triangles, all of which commonly appear on the ACT.
In this section, we will define and describe all the different kinds of triangles you’ll see on the test. In the next section, we will go through all the formulas you’ll need to know for your ACT triangle problems, as well as how to use them.
Equilateral Triangles
An equilateral triangle is a triangle that has three equal legs and three equal angles. Though the leg measurements can be anything (so long as they are all equal), the angle measurements must all equal 60°. Why? Because a triangle’s angles must always total 180°, and $180/3 = 60$.
Isosceles Triangles
An isosceles triangle is a triangle in which two sides and two angles are equal.
The sides opposite equal angles will always be equal and the angles opposite equal sides will always be equal. This knowledge will often lead you to the correct answers for many ACT questions in which it seems you are given very little information.
(We will go through how to solve this problem later in the guide, but for now, note how it seems as if you are not given enough information. But, if you remember that angles opposite equal lines are also equal, then you’ll see that you now have exactly enough to solve the problem)
Right Triangles
A right triangle is a triangle in which one of the angles measures 90° (90° is a right angle). This means that the sum of the other two angles must be 90° as well, since a triangle’s angles always add up to 90°.
The leg opposite the 90° angle will always be the triangle’s hypotenuse. This is due to the fact that the 90° angle will always be the largest angle in a right triangle. (Why? Because two 90° angles would make a straight line, not a triangle.)
Special Right Triangles
There are many different kinds of right triangle and some are considered “special.” These are triangles that have set angles or side lengths and formulas to correspond with them. Understanding these types of triangles (and their formulas) will save you a significant amount of time as you go through your test.
We will go through the formulas that correspond with these types of triangles in the next section, but for now, let’s go through their definitions.
Isosceles Right Triangle
An isosceles right triangle is just what it sounds like--a right triangle in which two sides and two angles are equal.
Though the side measurements may change, an isosceles triangle will always have one 90° angle and two 45° angles. (Why? Because a right triangle has to have one 90° angle by definition and the other two angles must add up to 90°. So $90/2 = 45$.)
30-60-90 Triangles
A 30-60-90 triangle is a special right triangle defined by its angles. It is a right triangle due to its 90° angle, and the other two angles must be 30° and 60°.
3-4-5, and 5-12-13 Right Triangles
3-4-5 and 5-12-13 triangles are special right triangles defined by their side lengths. The numbers 3-4-5 and 5-12-13 describe the lengths of the triangle’s legs, meaning that, when you have a right triangle with two leg lengths of 4 and 5, then you automatically know that the third leg equals 3. Any consistent multiples of these numbers will also work the same way. So a right triangle could have leg lengths of:
3(1)-4(1)-5(1) => 3-4-5
3(2)-4(2)-5(2) => 6-8-10
3(3)-4(3)-5(3) => 9-12-15
And so on.
These are considered special right triangles because all their sides are integers.
Now it's triangle formula time!
Triangle Formulas
Now that you know what all your triangles will look like, let’s go through how to find missing variables and information about them.
You will not be given any formulas on the ACT, so you must know all of these formulas by heart. (For more on the formulas you’ll need for the ACT math section, check out our guide to the 31 formulas you must know before test day.)
But beyond memorizing your formulas, you also must take care to understand them--how they work and when. All the rote memorization in the world won’t help you if you don’t know when or how to apply them when solving your problems.
All Triangles
Area
$a = {1/2}bh$
$b$ is the base of the triangle, which is the length of any one of the triangle’s legs.
$h$ is the height of a triangle, found by drawing a straight line (at a 90° angle) from the base of the triangle to the opposite angle from the base.
This means that, in a right triangle, the height is the length of the leg that meets at a 90° angle to the base. In a non-right triangle, you must create a new line for your height.
Perimeter
$p = l_1 + l_2 + l_3$
Just like with any other kind of plane geometry figure, the perimeter of a triangle is the sum of its outer sides (the triangle’s three legs).
Right Triangles
Some triangle formulas apply specifically to right triangles, so let's take a look.
Pythagorean Theorem
$a^2 + b^2 = c^2$
The Pythagorean theorem allows you to find the side lengths of a right triangle by using the lengths of its other sides. $a$ and $b$ signify the shorter legs of the triangle, while $c$ is always the leg opposite the 90° angle (the hypotenuse).
According to the Pythagorean theorem, $a^2 + b^2 = c^2$. We know that the side with $y$ meters must be our hypotenuse, as it is opposite the 90 degree angle. This means that:
$a^2 + b^2 = c^2$
$4^2 + x^2 = y^2$
Now, we need to find $y$ in terms of $x$, which means we need to isolate our $y$.
$16 + x^2 = y^2$
$y = √{16 + x^2}$
Our final answer is E, $√{x^2 + 16}$
3-4-5 and 5-12-13 triangles (and their multiples) are special because you do not need to work through the pythagorean theorem in order to find the side measures of the third length. Remember, if two sides of a right triangle are 12 and 15, then you automatically know the third side is 9 (because $3(3)-4(3)-5(3) = 9-12-15$).
Though we can find the length of BC using the Pythagorean theorem, we can also simply know that it is 5. (Why? Because it is the hypotenuse of a right triangle with leg lengths of 3 and 4).
Now, we can set up a proportion to find the measure of side AE. The length of AE to its hypotenuse will be in proportion to the length of BD to its hypotenuse.
${AE}/20 = 3/5$
$5AE = 60$
$12$
Our final answer is B, 12.
Isosceles Right Triangle
$x, x, x√2$
Though you can find the missing side lengths of an isosceles triangle using the Pythagorean theorem, you can also take a shortcut and say that the equal side lengths are $x$ and the hypotenuse is $x√2$.
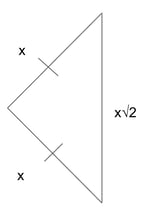
Why does this work? Let’s look at an isosceles right triangle problem.
It is given to us that one side length equals 10, so we know the second leg must also equal 10 (because the two legs are equal in an isosceles triangle). We can also find the hypotenuse using the Pythagorean theorem because it is a right triangle. So:
$10^2 + 10^2 = c^2$
$100 + 100 = c^2$
$200 = c^2$
$c = √200$
$c = √100 * √2$ (Why were we able to split up our root this way? Check out our guide to ACT advanced integers and its section on roots if this process is unfamiliar to you.)
$c = 10√2$
So, we are left with side lengths of 10, 10, and 10√2. Or, in other words, our side lengths are $x, x$, and $x√2$.
So our final answer is E, $10√2$
30-60-90 Triangle
$x, x√3, 2x$
Just like with an isosceles right triangle, a 30-60-90 triangle has side lengths that are dictated by a set of rules.
Again, you can find these lengths with the Pythagorean theorem, but you can also always find them using the rule: $x, x√3, 2x$, where $x$ is the side opposite 30°, $x√3$ is the side opposite 60°, and $2x$ is the side opposite 90°.
Make a note now of any formulas that are unfamiliar to you. You will need to know them by test day, so a little practice and organization now will go a long way to keeping them straight in your head.
Typical Triangle Questions
Most triangle question on the ACT will involve a diagram, though a rare few will be purely word problems. Let’s look at some of the standard types of question in each category.
Word Problems
Most triangle word problems are fairly simplistic once you draw them out. In fact, often times, the very reason why they give you the problem as a word problem instead of providing you with a diagram is because the test-makers thought the problem would be too easy to solve with a picture.
Whenever possible, draw your own diagram when you are given a triangle problem without one. It won’t take you long and it’ll be much simpler for you to visualize the question.
This should be a simple figure, but it never hurts to quickly sketch it out in order to keep all our parts in order.
We are told that this is a right triangle and we need to find one missing side length, so we will need to use the Pythagorean theorem.
$a^2 + b^2 = c^2$
Using our given side lengths for $a$ and $b$, we have:
$6^2 + 7^2 = c^2$
$36 + 49 = c^s$
$85 = c^2$
$c = √85$
Our final answer is G, $√85$
Diagram Problems
There are several different kinds of triangle problems that involve diagrams. Let’s break them into categories and discuss the strategies for each.
Diagram Type 1 - Finding Missing Values
Most triangle problems will fall into this category--you will be asked to find a missing angle, an area, a perimeter, or a side length (among other things) based on given information.
Some of these questions will be more complicated than others, but the ACT will always provide you will enough information to solve a problem, so it’s up to you to put the clues together.
Let’s walk through some real ACT math examples of this type:
Example 1,
First, let us fill in our given information so that we don't lose track of which angles measure what.
We know that the interior angles in a triangle sum up to 180 degrees, so we can find ACB by subtracting our givens from 180.
$180 - 30 - 110$
$40$
We also know that any straight line will measure 180 degrees. BCD are collinear, which means that they lie on a straight line. We can therefore find angle ACD by subtracting our ACB measure from 180.
$180 - 40$
$140$
Our final answer is G, 140°.
Example 2,
Similar triangles are in proportion with one another, so we can find the side lengths for triangle BAC by setting up proportions with triangle LKM.
${BA}/{AC} = {LK}/{KM}$
${BA}/3 = 12.5/7.5$
$7.5BA = 37.5$
$BA = 5$
And our second proportion will follow the same model.
${AC}/{BC} = {KM}/{LM}$
$3/{BC} = 7.5/15$
$7.5BC = 45$
$BC = 6$
Now, we have all the side measures for triangle BAC, which means we can find its perimeter.
$5 + 3 + 6$
$14$
Our final answer is B, 14.
Diagram Type 2 - Ratios and (In)Equalities
These kinds of questions will generally ask you to either find the ratios between parts of different triangles or will ask you whether or not certain sides or angles of triangles are equal or unequal.
We are told that AD is equal to BC, which means that their corresponding angles will also be equal. This means that angles CAB and DBA are equal (which consequently means that angles EAB and EBA are equal). We can therefore eliminate answer choice K.
Now, if angles CAB and DBA are equal, then angles CBA and DAB must ALSO be equal. Why? Well we know that each triangle has a 90 degree angle and one angle to equal to some unknown measurement (which we could call $x$). This means that the third, remaining, angle (let's call it $y$) must ALSO be the same for each triangle.
Each triangle would then be made up of:
$180 = 90 + x + y$
This means that we can eliminate answer choice J.
By that same reckoning, if angle DAB = angle CBA, then the legs opposite those angles must also be equal. This means that AC = BD, which means that answer choice F can be eliminated.
Because AD and CB are equal and both are part of a triangle with a hypotenuse of AB, legs CA and DB will cross in a manner that makes each half of the leg equal to the corresponding half of the leg of the other triangle. In other words, AE = EB and DE = EC. This means we can eliminate answer choice H.
The only answer choice we are left with is G. AD CANNOT equal AE. Why? AD is the leg of triangle ADE, while AE is the hypotenuse of that same triangle. From our definitions, we know that the hypotenuse must always be the longest side of the triangle and so it cannot be equal to one of the legs.
Our final answer is G.
Diagram Type 3 - Multi-Shape or Shapes Within Shapes
As you can see from earlier examples, some of the triangle problems on the ACT will involve multiple triangles (or other geometric shapes) combined together. This technique for presenting you problems is designed to challenge your understanding of lines and angles as well as triangles.
For these types of problems, you must use the information you are given and solve for more information down the line until you find exactly what you’re looking for. It’s essentially a domino effect of problem solving.
Because this problem uses variables, the simplest way to solve it is by plugging in our own numbers. So let us do so.
We are told that each unshaded triangle is a congruent right triangle. Because variables can be difficult to work with, let us replace $x$ with 4. (Why 4? Why not!)
This means that each triangle has one leg that measures 4 and one leg that measures $2(4) = 8$.
Now, we can find the length of one side of the square ABCD by adding our values together.
$4 + 8$
$12$
Each side of the square ABCD is equal to 12. Now we can find the total area by squaring this side measure, so:
$12^2$
$144$
The total area for ABCD is 144.
Now, because each unshaded triangle is a right triangle, we can find the side measures for the shaded square using the Pythagorean theorem.
$4^2 + 8^2 = c^2$
$16 + 64 = c^2$
$80 = c^2$
$c = √80$
Since this is the measure of one side of the shaded square, we can now find the area for the shaded square by squaring this number. So:
$√80)^2$
$80$
Now, we must simply divide our shaded square by our unshaded square, ABCD, in order to determine what fraction it is of the larger square.
$80/144$
$80 ÷ 16 = 5$ and $144 ÷ 16 = 9$
$5/9$
Our final answer is D, $5/9$
Life lessons and triangle strategies--win-win!
Strategies for Solving a Triangle Question
Because there are so many different kinds of triangle problems, it is difficult to break down one exact path for problem solving them.
That said, your greatest assets and strategies when solving triangle problems will be to follow these four steps:
#1: Write down your formulas
Because you are not given any formulas, you must keep them in your head and in your heart. The good news is that more you practice, the better you’ll be at rattling off triangle areas or side lengths of 30-60-90 triangles or anything else you’ll need.
But if you feel like you’ll forget your formulas as you go through your test, take a few seconds and write them down before you start solving your questions. Once you do, they will be there indelibly for you to work from for the rest of the math section, and you won’t have to worry about forgetting them.
#2: Use your formulas (and take your short-cuts)
Once you’re sure that you’ve remembered your formulas, using them is the absolute most crucial step for any triangle problem. And, considering that most of your formulas essentially act as short-cuts (why bother solving with the Pythagorean theorem when you know that the legs of a 30-60-90 triangle are $x, x√3, 2x$?), you will save yourself a great deal of time and energy when you can keep your formulas on hand and in order.
#3: When working with multi-shapes, break it into small steps
Remember that dealing with a multi-shape triangle problem is like working with dominoes. Each successive piece of information makes way for finding the next piece of information.
Don’t get intimidated that you don’t have enough information or that there are too many shapes or lines to deal with. You will always have enough data to go on--just focus on finding one shape and one piece of information at a time, and the dominoes will fall into place.
#4: Draw it out
Draw your own diagrams if you are given none. Draw on top of your diagrams when you are given pictures. Write in your givens and all the measurements you find along the way to your missing variable (or variables), mark congruent lines and angles.
The more you can clarify your diagrams, the less likely you’ll be to make careless errors in misplacing or confusing your numbers and equalities.
Ready to put your knowledge to the test?
Test Your Knowledge
Now let's test your triangle knowledge against some more real ACT math problems.
1)
2)
3)
4)
Answers: B, F, E, H
Answer Explanations:
1) Because we are told that this is an isosceles trapezoid, we know that each non-parallel side must be equal. This means that the angles that capture these sides (angles BDC and ACD) must also be equal.
We also know that the interior degrees of a triangle will always sum 180 degrees, so we can find the measure of DXC by subtracting our two known angles from 180.
$180 - 25 - 25$
$130$
Now, DB is a straight line, which means that the angles that make the line must total 180 degrees. This means we can find angle BXC by subtracting our known angle from 180.
$180 - 130$
$50$
Finally, we again know that a triangle's interior angles will sum to 180, so we can find DBC by subtracting our known angles from 180.
$180 - 50 - 35$
$95$
Our final answer is B, 95°.
2) We know from our triangle definitions that the larger the side opposite an angle, the larger the angle will be. (If you ever feel unsure about the relationships between angles and sides of a triangle, you can also consult your rules and definitions of trigonometry.)
So if we drew in some random side measurements for XZ and YZ (so long as they follow the rule that XZ > YZ), we can see clearly that angle Y will be greater than angle X.
Our final answer is F, angle X < angle Y.
3) We are told that the triangle is a hypotenuse right triangle, which means that we can use our shortcuts to find the other two side lengths.
We know that an isosceles right triangle has side lengths of $x, x$, and $x√2$. Since we already know that the hypotenuse is $8√2$, we can say that the other two sides both measure 8.
Now, we can add together the legs to find the perimeter.
$8 + 8 + 8√2$
$16 +8√2$
Our final answer is E, $16 + 8√2$
4) Before we do anything else, let us fill in our given information.
Now, we can know the triangles and the exterior angle are all collinear, which means that the angles that create the line will sum to 180°. This means we can find angle CBD by subtracting our exterior angle from 180.
$180 - 140$
$40$
Now that we have two interior angle measures in triangle DCB, we can find the measure of the third (because the interior angles in a triangle will always add up to 180).
$180 - 40 - 47$
$93$
[Note: you may notice that the sum of the two angles not touching the exterior angle sum up to equal the exterior angle--$47 + 93 = 140$. This is not a coincidence. It will always be the case that the two non-connected angles will sum to equal the exterior angle of any type of triangle.)
Now we again have two angles that create a straight line, which means that we can find the measure of angle CDA by subtracting our known angle from 180°.
$180 - 93$
$87$
And finally, CAD forms a triangle, which means that its interior angles will sum to equal 180. We can find angle ACD by subtracting our two known values from 180°.
$180 - 76 - 87$
$17$
Our final answer is H, 17°.
Aw, yea. You've earned that nap.
The Take-Aways
Whether it be a trigonometry problem or a geometry problem, you’ll see triangles several times on any given ACT. Though most triangle problems are fairly straight forward, you’ll need to know the basic building blocks of triangles and geometry in order to understand how to solve them.
Know your definitions, memorize your formulas, and do your best to keep a clear head as you go through your test. And, as always, practice, practice, practice! The more experience you get in solving the variety of triangle questions the ACT can think to put in front of you, the better off you’ll be.
What’s Next?
Whoo! You took on triangles and won (give yourself a round of applause)! In the mood for more geometry? Hop on over to our guides on ACT circles, polygons, and solid geometry and round off all your geometry studies in one go.
Not sure what topic to tackle next? Make sure you've got a clear idea of all the math topics you'll be tested on and check out all of our ACT math guides for reference and practice. Each guide has definitions, formulas, and real ACT practice questions and will break down the solving process step-by-step.
Been procrastinating? Check out our guide on how to take back your study time and beat back those procrastination demons.
Looking to get a perfect score? Our guide to getting a 36 on the ACT math (written by a perfect-scorer!) will help get you where you need to go.
Want to improve your ACT score by 4 points?
Check out our best-in-class online ACT prep program. We guarantee your money back if you don't improve your ACT score by 4 points or more.
Our program is entirely online, and it customizes what you study to your strengths and weaknesses. If you liked this Math lesson, you'll love our program. Along with more detailed lessons, you'll get thousands of practice problems organized by individual skills so you learn most effectively. We'll also give you a step-by-step program to follow so you'll never be confused about what to study next.
Check out our 5-day free trial:
Have friends who also need help with test prep? Share this article!
Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.
Holly R.