
Reflections, rotations, translations, oh my! Whether you’re dealing with points or complete shapes on the coordinate plane, you can spin 'em, flip 'em, or move 'em around to your heart’s content. And, often enough, you’ll be asked to do so on the ACT.
This will be your complete guide to rotations, reflections, and translations of points, shapes, and graphs on the ACT—what these terms mean, the types of questions you’ll see on the test, and the tips and formulas you’ll need to solve these questions in no time.
Before You Continue
Reflection, rotation, and translation problems are fairly rare on the ACT, only appearing once per test, if at all. If you’re shooting for a perfect or nearly perfect score and want to make sure you have all your bases covered, then this is the guide for you.
But if you still need to brush up on your fundamentals, then your focus will be better spent on studying the more common types of math problems you’ll see on the test. Remember, each question is worth the same amount of points, so it is better that you can answer three or four questions on integers, triangles, or slopes than to answer one question on rotations.
So if you’ve got a solid grasp of all your foundational math topics (or you just really, really like coordinate geometry), then lets talk reflections, rotations, and translations!
What is a Reflection?
A reflection in the coordinate plane is just like a reflection in a mirror. Any point or shape can be reflected across the x-axis, the y-axis, or any other line, invisible or visible. This line, about which the object is reflected, is called the "line of symmetry."


Let's look at a typical ACT line of symmetry problem.

To find our lines of symmetry, we must divide our figure into symmetrical halves. This means that each side must be a reflection of the other, about a line.
If we connect opposite angles in our figure, we will have several lines of symmetry. Let us do so.

Now, from here, we can see that there are also lines of symmetry between our interior angles, like so:

If we put them together, we get this.

But wait! We can count our total number of lines (diameters, since they're spanning the entire length of the circle), but we CANNOT count each individual point that connects to the circumference of the circle as a line of symmetry. The number of actual lines of symmetry will be half the number of connecting points, because we need to only count each line one time.
Because this is a busy figure, let us look at it a little more simplistically.

Here, we have gotten rid of the other half of each line of symmetry and transformed them into all the radii of the circle. Now we can count the lines of symmetry without fear that we are double-counting one line.
If we count them as they are, we can see that there are eight lines of symmetry total.
Our final answer is H, 8.
 Nature's take on lines of symmetry in action.
Nature's take on lines of symmetry in action.
What is a Rotation?
Objects in the coordinate plane can also be rotated (turned) clockwise or counterclockwise. Imagine that we can adjust the object with our hands—it will spin, while still lying flat, like a piece of paper on a tabletop.
We must always select a point to act as the center point for our rotation. This center point of our rotation can be anywhere on the coordinate plane or on the shape in question (notice that it does NOT have to be the center of the shape).
Let us look at a visual demonstration of this.
We can have an object that rotates about its own center.



A trapezoid is rotating about its center.
Or the same shape can also be rotated about a different point.



Here, the trapezoid is rotating about a point on the base of the trapezoid.
But on the ACT, you'll almost always be asked to rotate an object "about the origin." This means that the origin (coordinates $(0,0)$) acts as your center of rotation.



The angle about which the object moves is called the angle of rotation. As we rotate an object, the angle of rotation will be:
- Positive when we move the object counterclockwise
- Negative when the object is rotating clockwise.

A positive angle of rotation.

A negative angle of rotation.
You can see that our shape ended up in the same place, but it got there by being rotated either $+180°$ or $-180°$.
On the other hand, sometimes the ACT will have you rotate objects in a way that runs counter to these standard rules. Always follow the given instructions, even if they seem to contradict mathematical laws.
For instance,

(We will walk through this question later in the guide)
We will walk through how to solve this question later in the guide, but for now notice that the question asks you to rotate the circle 90 degrees clockwise. Really, the degree measure would be $-90$ degrees, even though it is technically correct to say that you’re moving $+90$ degrees in a certain direction.
Because this can be confusing and seemingly contradicts the rules of rotation degrees (though technically does not), just follow the information you are given in the question, rather than trying to overcomplicate the problem.
As you might also guess from the above question, if you are asked to rotate an object on the ACT, it will be at an angle of 90 degrees or 180 degrees (or, more rarely, 270 degrees). These are nice numbers that evenly divide the coordinate plane into four parts, and each of these degree measures has a standard rule of rotation, when rotating a point about the origin.
Let us look at these rotation rules.

Some rules are more helpful than others. Rotation rules and formulas happen to be quite useful.
Rotation Rules/Formulas
Whether you are asked to rotate a single point or a full object, it is easiest to rotate the point/shape by focusing on each individual point in question. You can determine the new coordinates of each point by learning your rules of rotation for certain angle measures.
Each of the three degree measures—90, 180, or 270—will shift the coordinates of your original point to a different, calculable, position on the graph. If rotating counterclockwise (a positive angle of rotation), you can use these rules to find your new coordinate points.
If you're a little rusty on which quadrants of the $xy$-coordinate plane have positive and negative $x$- and $y$-coordinates, you should take a quick detour to our article on graph quadrants before moving on.
[Note: these formulas only apply when rotating an object about the origin. If you are asked to rotate objects about another center of rotation (as with the circle question above), these rules will NOT apply.]
Let us say we begin with a point at coordinates $(8, 3)$.
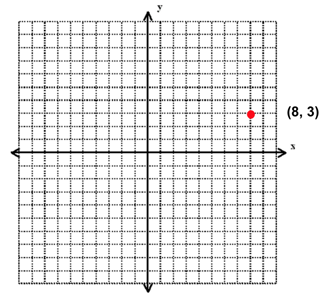
For 90 degree rotations:
$(a, b)$ => $(-b, a)$

A 90° rotation bring our original coordinates of $(8, 3)$ to $(-3, 8)$.
For 180 degree rotations:
$(a, b)$ => $(-a, -b)$

A $180°$ rotation brings our original coordinates of $(8, 3)$ to $(-8, -3)$.
For 270 degree rotations:
$(a, b)$ => $(b, -a)$

A $270°$ rotation brings our original coordinates of $(8, 3)$ to $(3, -8)$.
(And, of course, a 360 degree rotation will bring you right back to the beginning at $(a, b)$ again!)

A $360°$ rotation bring our original coordinates of $(8, 3)$ back to $(8, 3)$ once again.

Keep your head on you—those rotations can be a doozy!
What is a Translation?
In addition to reflecting or rotating an object, we can also translate the object to another place on the coordinate plane. Translation is the act of "sliding" our point or shape along the coordinate plane in a particular direction.
The shape can be translated up or down (or both!) any amount of distance along the plane. It maintains its shape and bearing, but is simply located elsewhere in the plane.

The way to notate that a translation is to occur is to say:
$T_{a,b}(x,y)$
This means that your final coordinates for this point will be:
$(x+a,y+b)$
For example,
What is the new point for $T_{5,−2}(−3,6)$?
A. $(3, 3)$
B. $(2, 4)$
C. $(-3, 6)$
D. $(11, -5)$
E. $(-1, -2)$
We know that we must add together our translated points to the corresponding $x$ and $y$ values of our original coordinates. So:
$T_{5,−2}(−3,6)$
$(−3+5,6+−2)$
$(2,4)$
Our new coordinates for this point are at $(2, 4)$
You can see why this is true if we look at it on a graph.
Here, we have our starting point of $(-3, 6)$.

Now, we are moving positively (to the right) 5 spaces and negatively (downwards) 3 spaces. If we started at $(-3, 6)$, this wll put our new point at $(2, 4)$.

Our final answer is B, $(2, 4)$.
Typical Reflection, Rotation, and Translation Problems
Again, these types of questions are fairly rare on the ACT, and you will only ever see one question on reflections, rotations, or translations, if indeed you see any at all.
That said, there are four different types of reflection/rotation/translation problems that will show up, when they appear. These questions will be either a reflection, rotation, or translation questions about:
#1: Points
#2: Shapes in the coordinate plane
#3: Function graphs
#4: Shapes and their lines of symmetry
Let’s look at all three.
Points
Because a point is individual, points are the simplest objects to be rotated, reflected, or translated. Each point will always be made up of an $x$ and $y$ coordinate—written $(x,y)$—but you only have to keep track of the solitary point and how it should shift and move, rather than having to keep track of it in relation to other points (as you will have to when working with shapes).
Shapes
Shapes are slightly more complicated to reflect or rotate than points are, due to the fact that all the points on a shape (and the lines connecting those points) will have a relationship with one another that must be maintained or altered in a controlled manner. This means that any shape rotation/reflection/translation will require more consideration and care, in order to make sure all your pieces are properly aligned.
It is often much easier, when working with modified shapes, to map out the positions of the points alone. Don’t worry about the lines—mark the proper position of the new coordinates for the points and the lines will fall into place.
Let's look at an example.

The red line makes up one side of the trapezoid above. If this line has a slope of $3/2$, what is the slope of the line when the trapezoid is reflected across the $x$-axis?
A. $−2/3$
B. $−3/2$
C. $2/3$
D. $3/2$
E. $4/3$
Instead of focusing on the slopes themselves, let us map out the new trapezoid by its points and only then connect the lines.

Now, if we connect the lines to actually make the trapezoid...

We can find the new slope of the line by counting the rise of over the run.
The rise is $-3$ and the run is $+2$. The new slope of the equivalent line in our trapezoid will be $−3/2$.
Our final answer is B, $−3/2$
Function Graphs
Function graphs can be reflected or translated just like shapes and points, though they CANNOT be rotated. (Why can functions not be rotated? If a function were rotated, it would fail the vertical line test (more on this is covered in our guide to ACT functions) and no longer be a function.)

A reflected function.

A translated function.

A function CANNOT be rotated. A graph with more than one $y$ value (output) for the same $x$ value (input) is NOT a function.
Function Translations
We can translate our function up or down by adding or subtraction from our output.
Adding to output translates the graph up.

If this is the original placement of our graph, $f(x)$....

We can translate it up by adding to the output, aka $f(x)+5$.
Subtracting from the output, on the other hand, moves the graph down.

Again, if this is the original placement of our graph, $f(x)$....

We can translate it down by subtracting from the output, aka $f(x)−5$.
This kind of translation will work on any function graph.

We can also translate a function side to side (horizontally) by adding or subtracting from the input.
Adding to the input will shift the graph left.

If this is the placement of our original graph, $f(x)$...

We can translate it left by adding to the input, aka $f(x+5)$
Subtracting from the input will shift the graph to the right.

Again, if this is our original graph, $f(x)$...

We can translate it right by subtracting from our input, aka $f(x−5)$
This kind of translation will work on any function graph as well.

Function Reflections
We can also reflect our function about a line of symmetry along the $x$ or $y$-axis.
Making the output negative makes the function reflect across the $x$-axis (inverts it about the $x$-axis).
$f(x)$ becomes $−f(x)$.

Making input negative makes the function reflect across the $y$-axis.
$f(x)$ becomes $f(−x)$

Lines of Symmetry
As we saw with our earlier line of symmetry problem, the ACT will sometimes present you with a picture and ask you to identify the lines of symmetry.
If you understand how a line of symmetry works (that everything on each half of the line must be symmetrical, i.e. a reflection), and you make sure to count each line only once, then you should be able to breeze through these questions without fail.

If you feel you are in information overload right now, don't worry! You can always make notes and flashcards to review and memorize later; just understanding how and why rotations and translations work is enough for now.
Strategies for Reflection and Translation Problems
Though no two reflection/translation/rotation problems are exactly alike, there are a few tips and tricks to follow for any kind you may come across.
#1: Draw your own graphs
Sometimes you will be given a diagram, or half a diagram, and sometimes you won't. But always, when the test asks you to reflect, rotate, or translate a point or a shape, you must form your own new picture, either on the page or in your head.
Because it is entirely too easy to make mistakes when working out math problems in your head alone, it is always a good idea to take a moment to sketch out a graph of the object’s new position in space (if not the old one as well).
Seeing a diagram on the page is especially useful if you are asked to find more information, rather than simply identifying a new coordinate point (a feat in and of itself!). For instance, you might be asked to find the slope of a reflected or rotated line (as we saw above), or the product of two translated $x$-coordinates, or anything else the ACT might think of.
Without making your own drawings and diagrams, it can be easy to become confused, fall for bait answers, and lose precious points.
#2: Drill your rotation formulas
When working with translations or reflections, it is simple enough to draw your own picture and line up your corresponding points, but when it comes to rotations, it can be much harder to visualize the movement of the point or the object. Even when you’ve mapped out the original point, rotations are often much trickier than they appear.
Unless you have a paper cut-out of your point, shape, or function and want to spend your time spinning your scratch paper around in circles, it’s better to simply memorize your rotation rules for 90, 180, and 270 degrees.
#3: Double-check, double-check, (triple-check)
Rotations, reflections, and translations may seem simple (and, indeed, the underlying principles are not any more complex than anything else on the ACT), but the difficulty in solving these kinds of problems is in just how easy it is to mis-map a coordinate point or two. It is especially precarious, because the test-makers will throw as many bait answers at you as they possibly can.
Nothing is more frustrating than when you know how to solve a problem, but go too quickly or too carelessly through your test and so end up getting the question wrong. Make sure you double-check that you’ve properly shifted your coordinates before you bubble in that final answer.

Excited to do some practice questions?
Test Your Knowledge
Now let's test your knowledge on some real ACT math questions on reflections, translations, and rotations.
1.

When $ABCD$ is reflected over the $y$-axis to $A'B'C'D'$, what are the coordinates $D'$?
F. $(-12, 1)$
G. $(-12,-1)$
H. $(12,-1)$
J. $(1,12)$
K. $(1,-12)$
2. The graph $y=f(x)$ is shown below.

What could be the graph of $y=f(x−4)$?
A.

B.

C.

D.

E.

3.

4.

Answers: F, B, K, C
Answer Explanations:
1. Because we need to reflect our trapezoid, let us draw ourselves a picture.
Note: be very careful to reflect your shape around the correct axis. The way the diagram is laid out, you may be tempted to reflect your object across the $x$ axis, like so

This will give you the wrong answer and lead you to fall into one of the bait answer traps.
Because we are told to reflect the trapezoid across the $y$ axis, our graph will instead look like this:

You can see, then, that the reflection of point D will be at coordinates $(-12, 1)$
Our final answer is F, $(-12, 1)$
2. Because we are being asked to find $y=f(x−4)$ from our original $y=f(x)$, we are subtracting from our input value. (For more on function inputs and outputs, check out our guide to ACT functions).
If you remember our definitions on how to translate functions from above, you know that subtracting from the input translates our graph to the right and has no affect on the height (meaning, the graph does not move up or down). The only graph example that moves the function to the right and does not move it up or down is answer choice B.
Again, here is our original graph.

And here is the graph for answer choice B.

Our final answer is B.
3. We are supposed to reflect our given triangle, so let us use our most important strategy and draw our picture out, so that we won’t make any mistakes trying to do the problem in our heads.

Once we have reflected our triangle about the line of symmetry x, we can see that the perimeter is made of:
$y+z+z+y$
$2y+2z$
Or, in other words,
$2(y+z)$
Our final answer is K, $2(y+z)$
4. We are being told to rotate the point $(6, 6)$ on the circle 90 degrees clockwise about the center of rotation $(2, 3)$.
Because we are not rotating our point about the origin, our rotation rules unfortunately will not apply to this problem. That means we must find another way to rotate our point 90 degrees clockwise.
By far, the simplest way to solve this problem is to divide our circle into four by drawing two diameters perpendicular to one another. (Why divide the circle into four? A circle is 360 degrees, and $360/90=4$

By dividing our circle this way, we can see that a 90 degree rotation would put the point slightly below the x-axis at coordinates approximately $(5, -1)$.
Our final answer is C, $(5, -1)$

Phew! That wasn't so hard, now was it?
The Take Aways
Though rare(ish), the occasional rotation, reflection, or translation question can certainly throw you for a loop if you’re unprepared for it. But nothing the ACT can put on the test is unsolvable (and, indeed, the test is designed to give you opportunities to succeed, even as it tests your diligence and eye for detail).
Once you’ve got your basic building blocks and formulas down tight, you will be well on your way to mastering all your coordinate geometry questions and earning that perfect score.
What’s Next?
You’ve tackled reflections, translations, and rotations (go you!), so take a minute to look over all the math topics on the ACT. Making sure you’re prepared for whatever comes your way is most of the battle, so look to our individual ACT math guides—all of which have real practice questions!—to brush up on any weak areas in your mathematical portfolio.
Want to master two of the most invaluable math strategies for mastering the ACT? Check out our guides on how to use plugging in numbers and plugging in answers to make sense of some of the trickiest ACT problems out there.
Looking to get that perfect score? Look no further than our guide to getting a perfect 36 on the ACT math, written by a perfect scorer.











