 You’ve dealt with the basics of coordinate geometry and points (and if you haven’t already, you may want to take a minute to refresh yourself) and now it’s time to look at the ins and outs of lines and slopes on the coordinate plane.
You’ve dealt with the basics of coordinate geometry and points (and if you haven’t already, you may want to take a minute to refresh yourself) and now it’s time to look at the ins and outs of lines and slopes on the coordinate plane.
This will be your complete guide to lines and slopes--what slopes mean, how to find them, and how to solve the many types of slope and line equation questions you’ll see on the ACT.
What are Lines and Slopes?
If you’ve gone through the guide on coordinate geometry, then you know that coordinate geometry takes place in the space where the $x$-axis and the $y$-axis meet. Any point on this space is given a coordinate point, written as $(x, y)$, that indicates exactly where the point is along each axis.
A line (or line segment) is a marker that is completely straight (meaning it has no curvature). It is made up of a series of points and and connects them together.
A slope is how we measure the slant/steepness of a line. A slope is found by finding the change in distance along the y axis over the change in distance along the x axis.
You have probably heard how to find a slope by finding the "rise over run." This means exactly the same thing--change in $y$ over change in $x$.
$${\change \in y}/{\change \in x}$$
Let's look at an example:
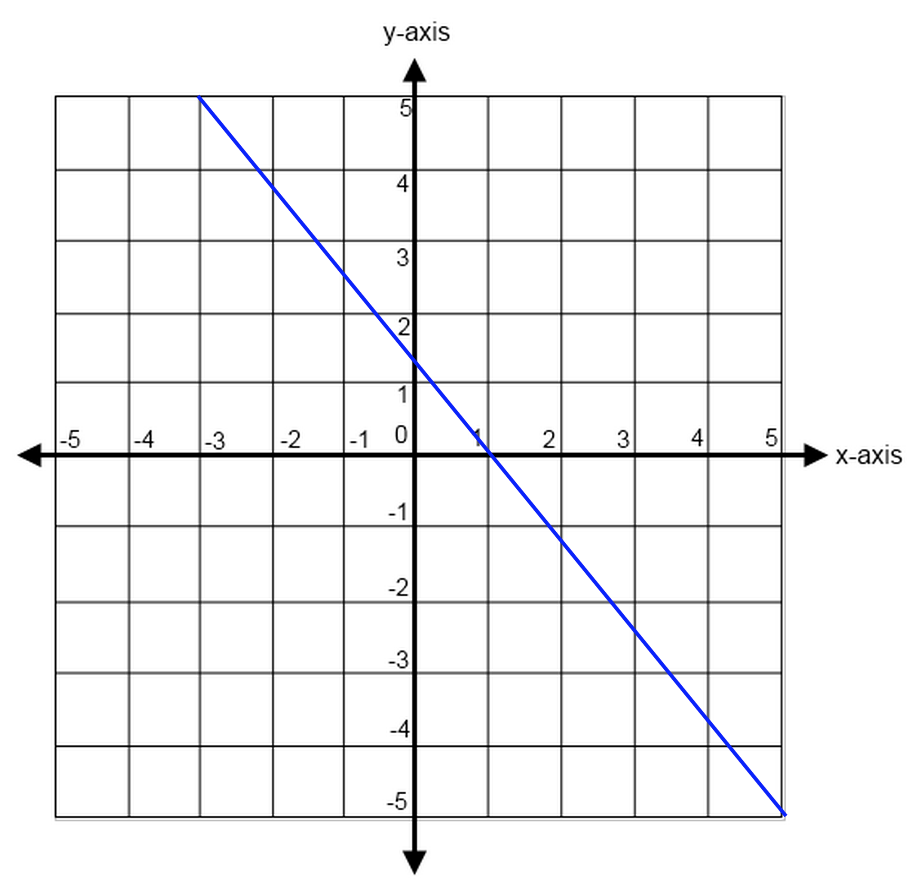
Say we are given this graph and asked to find the slope of the line.
We must see how both the rise and the run change. To do this, we must first mark points along the line to in order to compare them to one another. We can also make life easier on ourselves by marking and comparing integer coordinates (places where the line hits at a corner of $x$ and $y$ measurements.)
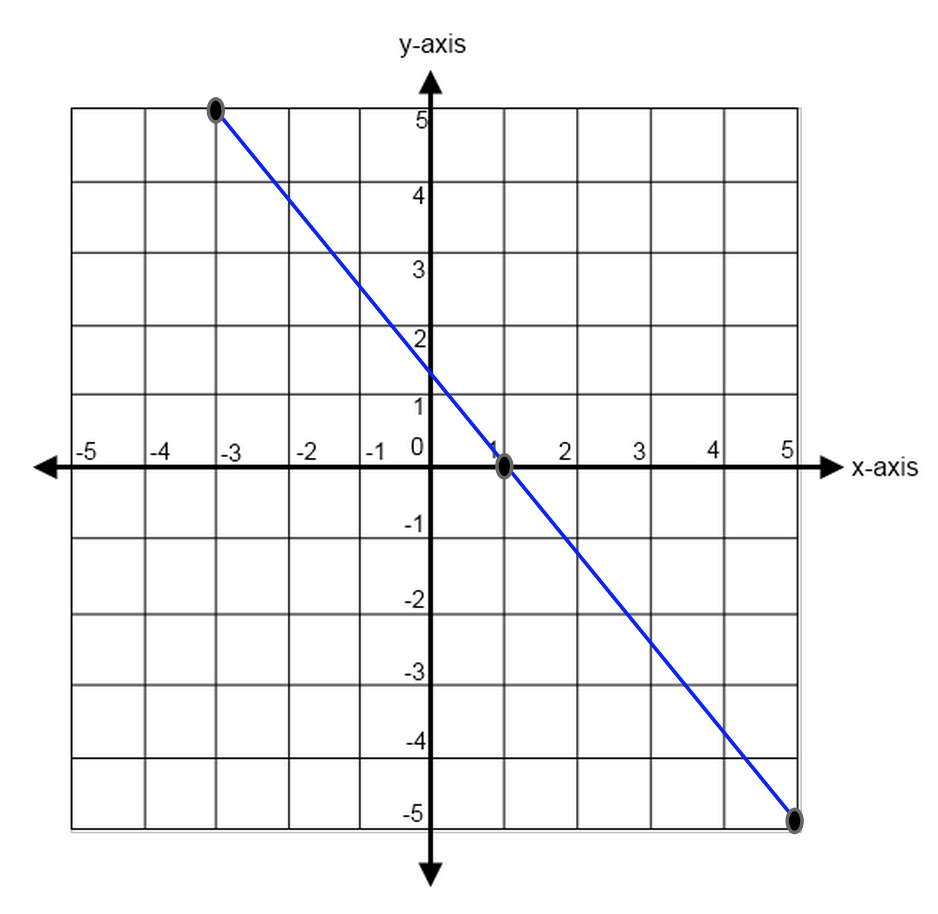
Now we have marked our coordinate points. We can see that our line hits at exactly: $(-3, 5)$, $(1, 0)$, and $(5, -5)$.
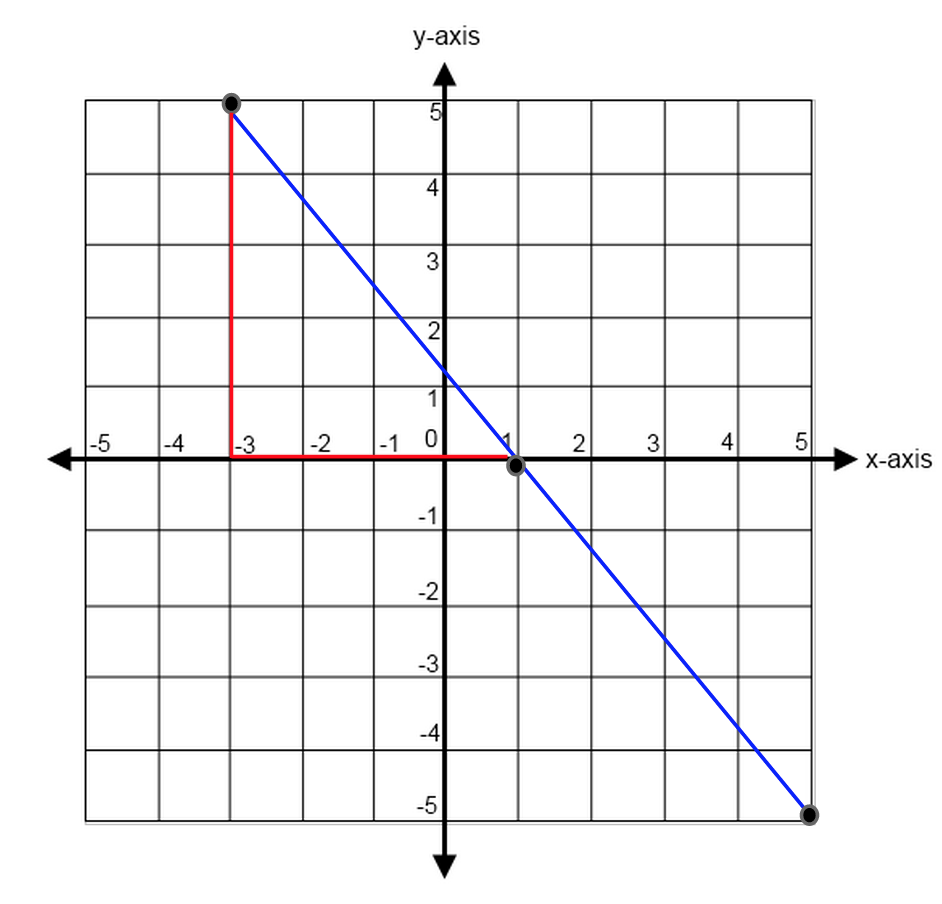
In order to find the slope of the line, we can simply trace our points to one another and count. We've highlighted in red the path from one coordinate point to the next.
You can see that the slope falls (has a negative "rise") of 5. This means the rise will be -5.
The slope also moves positively (to the right) 4. Thus, the run will be +4.
This means our slope is:
$-{5/4}$
Properties of Slopes
A slope can either be positive or negative.
A positive slope rises from left to right.
A negative slope falls from left to right.
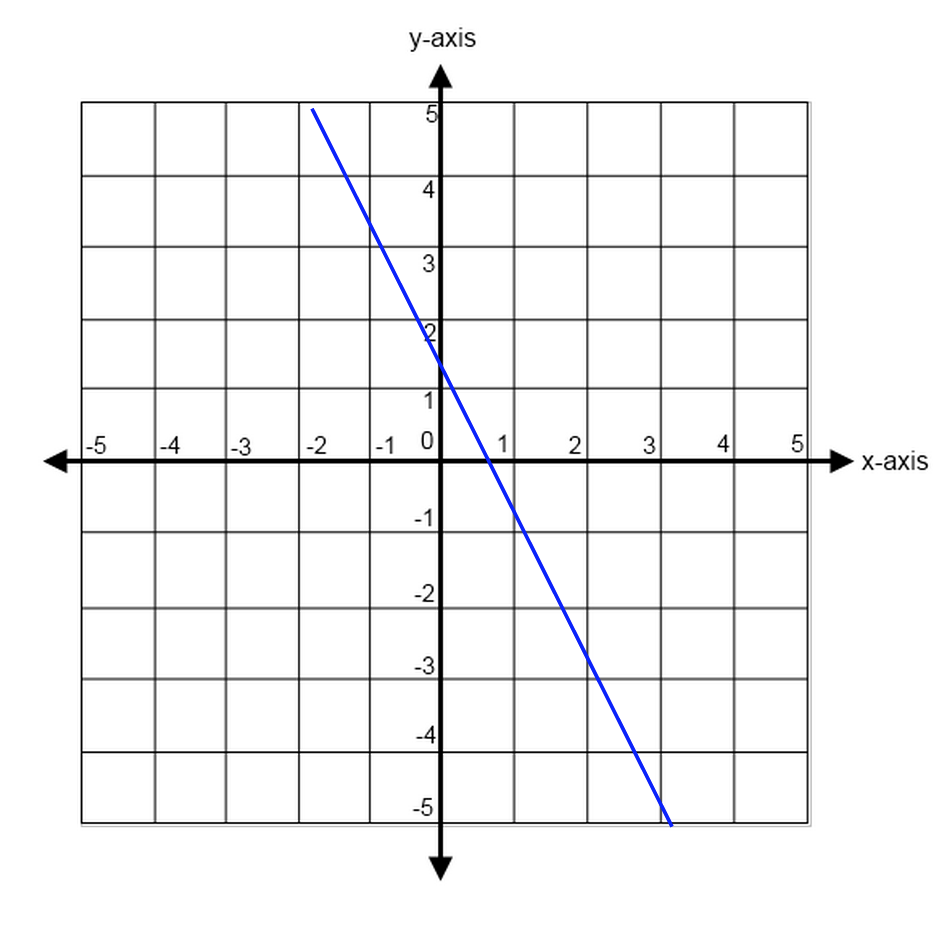
A straight line has a slope of zero. It will be defined by one axis only.
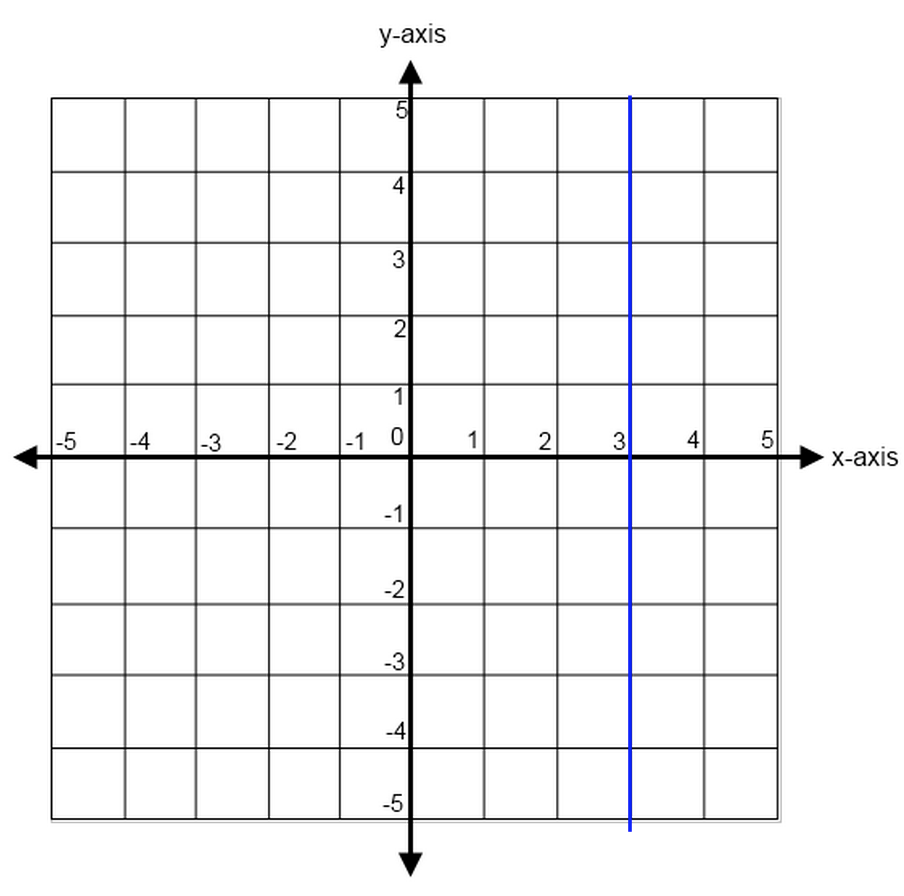
$x = 3$
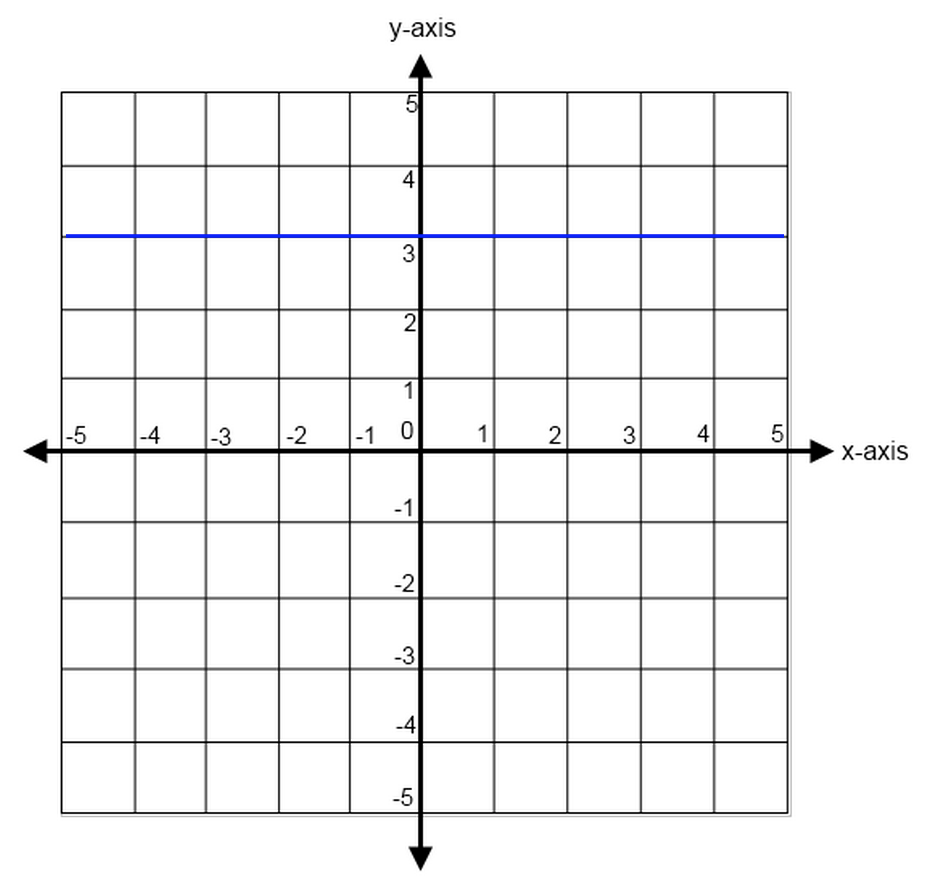
$y = 3$
The steeper the line, the larger the slope.
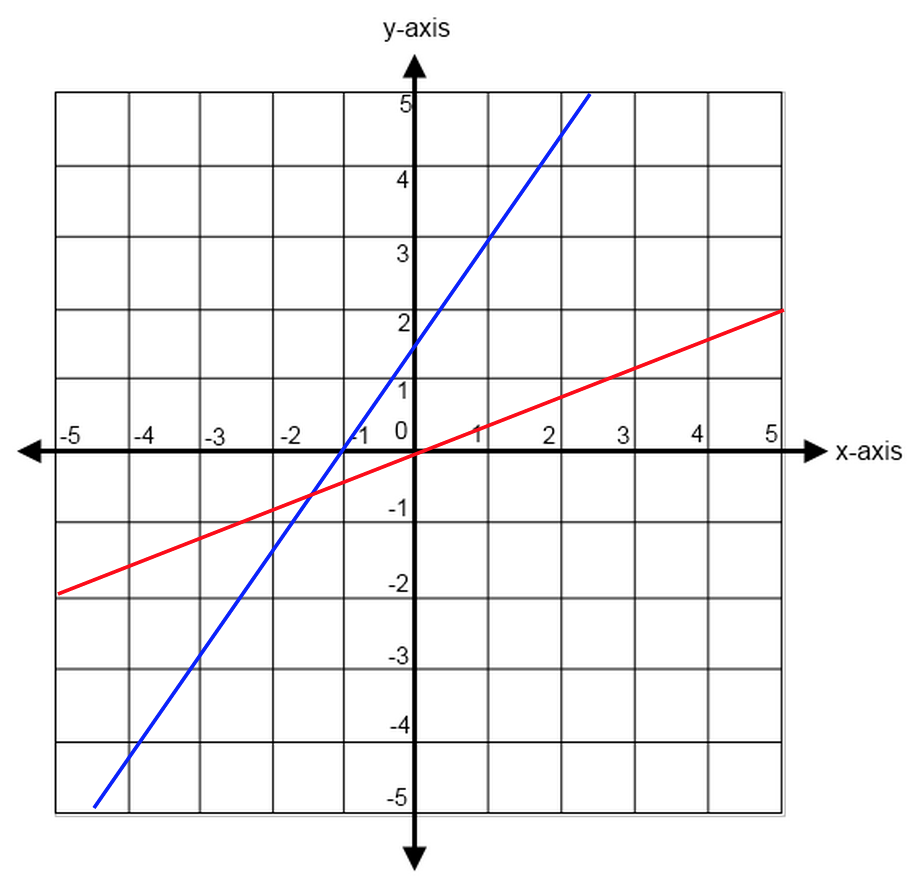
The blue line is steepest, with a slope of $3/2$. The red line is shallower, with a slope of $2/5$

Now that we've gone through our definitions, let us take a look at our slope formulas.
Line and Slope Formulas
Finding the Slope
$${y_2 - y_1}/{x_2 - x_1}$$
In order to find the slope of a line that connects two points, you must find the change in the y-values over the change in the x-values.
Note: It does not matter which points you assign as $(x_1, y_1)$ and $(x_2, y_2)$, so long as you keep them consistent.
Find the slope of the line with coordinates at (-1, 0) and (1, 3).
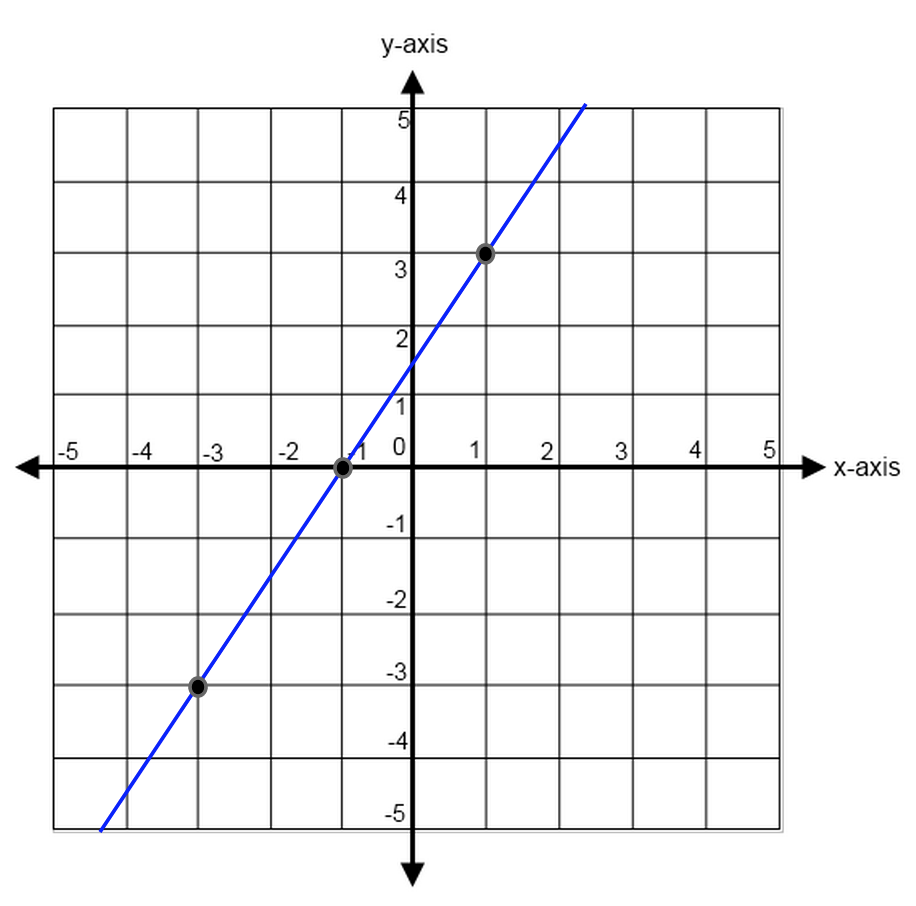
Now, we already know how to count to find our slope, so let us use our equation this time.
${y_2 - y_1}/{x_2 - x_1}$
Let us assign the coordinate (-1, 0) as $(x_1, y_1)$ and (1, 3) as $(x_2, y_2)$.
$(3 - 0)/(1 - -1)$
$3/2$
We have found the slope of the line. Now let's demonstrate why the equation still works had we switched which coordinate points were $(x_1, y_1)$ and which were $(x_2, y_2)$.
This time, coordinates (-1, 0) will be our $(x_2, y_2)$ and coordinates (1, 3) will be our $(x_1, y_1)$.
${y_2 - y_1}/{x_2 - x_1}$
$(0 - 3)/(-1 - 1)$
${-3}/{-2}$
$3/2$
As you can see, we get the answer $3/2$ as the slope of our line either way.
The Equation of a Line
$$y = mx + b$$
This is called the “equation of a line,” also known as an line written in "slope-intercept form." It tells us exactly how a line is positioned along the x and y axis as well as how steep it is.
This is the most important formula you’ll need when it comes to lines and slopes, so let’s break it into its individual parts.
- $y$ is your $y$-coordinate value for any particular value of $x$.
- $x$ is your $x$-coordinate value for any particular value of $y$.
- $m$ is the measure of your slope.
- $b$ is the $y$-intercept value of your line. This means that it is the value along the $y$-axis that the line hits (remember, a straight line will only hit each axis a maximum of one time).
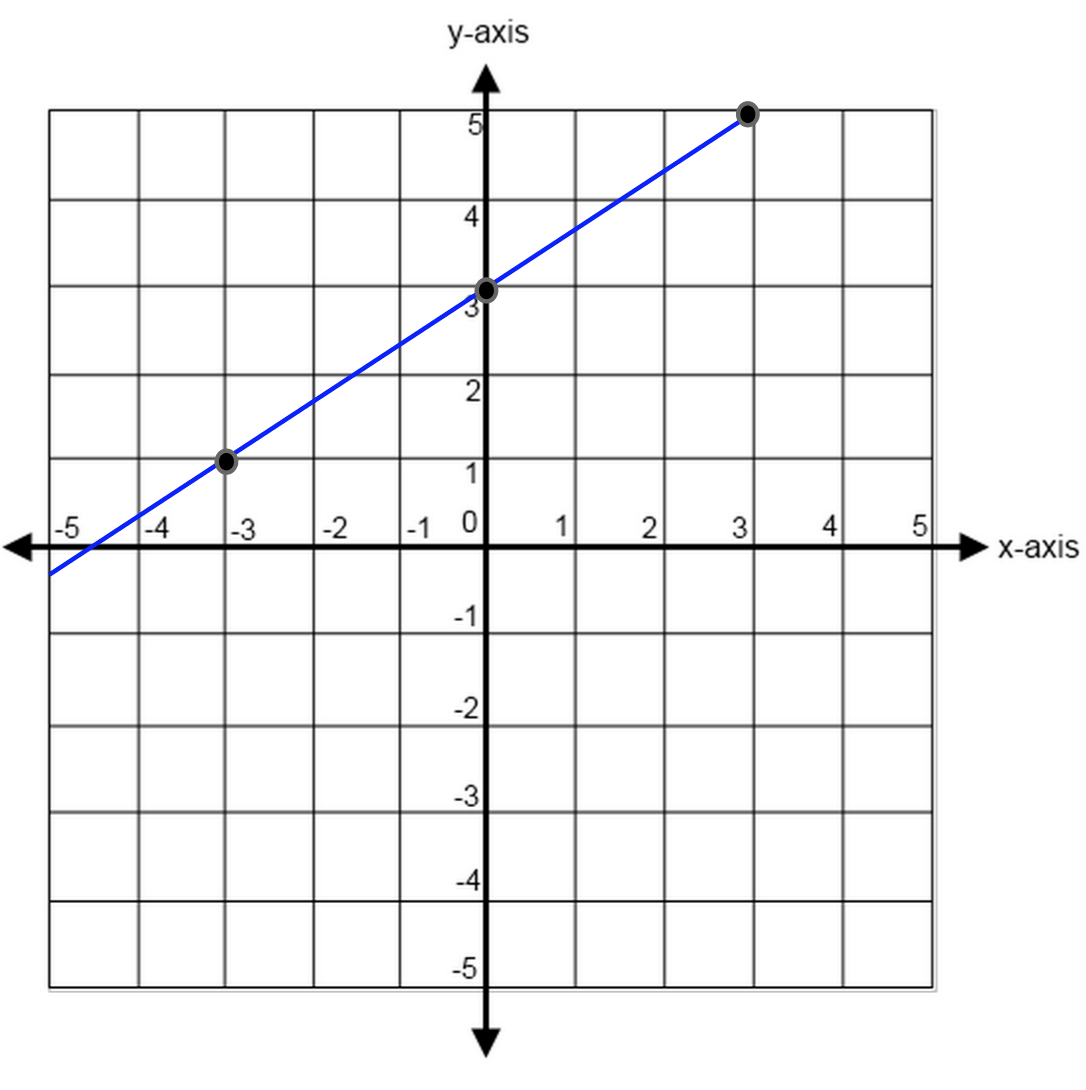
For this line, we can see that the y-intercept is 3.
We can also count our slope out or use two sets of coordinate points (for example, $(-3, 1)$ and $(0, 3)$) to find our slope of $2/3$.
So when we put that together, we can find the equation of our line at:
$y = mx + b$
$y = {2/3}x + 3$
Remember: always re-write any line equations you are given into this form! The test will often try to trip you up by presenting you with a line NOT in proper form and then ask you for the slope or y-intercept. This is to test you on how well you're paying attention and get people who are going too quickly through the test to make a mistake.
What is the slope of the line $3x + 12y = 24$?
First, let us re-write our problem into proper form:
$y = mx + b$
$3x + 12y = 24$
$12y = -3x + 24$
$y = -{3/12}x + 24/12$
$y = -{1/4}x + 2$
The slope of the line is $-{1/4}x$
Now let’s look at a problem that puts both formulas to work.
For some real number A, the graph of the line $y=(A+1)x +8$ in the standard $(x,y)$ coordinate plane passes through $(2,6)$. What is the slope of this line?
A. -4
B. -3
C. -1
D. 3
E. 7
In order to find the slope of a line, we need two sets of coordinates so that we can compare the changes in both $x$ and $y$.
We are given one set of coordinates at $(2, 6)$ and we can find the other by using the $y$-intercept.
The $b$ in the equation is the y-intercept (in other words, the point at the graph where the line hits the y-axis at $x = 0$). This means that, for the above equation, we also have a set of coordinates at $(0, 8)$.
Now, let’s use both sets of coordinates—$(2, 6)$ and $(0, 8)$—to find the slope of the line:
${y_2 - y_1}/{x_2 - x_1}$
$(8 - 6)/(0 - 2)$
$-{2/2}$
$-1$
So the slope of the line is -1.
Our final answer is C, -1.
(Note: don’t let yourself get tricked into trying to find $A$! It can become instinct when working through a standardized test to try to find the variables, but this question only asked for the slope. Always pay close attention to what is being asked of you.)
Perpendicular Lines
Two lines that meet at right angles are called “perpendicular.” Perpendicular lines will always have slopes that are negative reciprocals of one another.
This means that you must reverse both the sign of the slope as well as the fraction.
For example, if a two lines are perpendicular to one another and one has a slope of 4 (in other words, $4/1$), the other line will have a slope of $-{1/4}$.
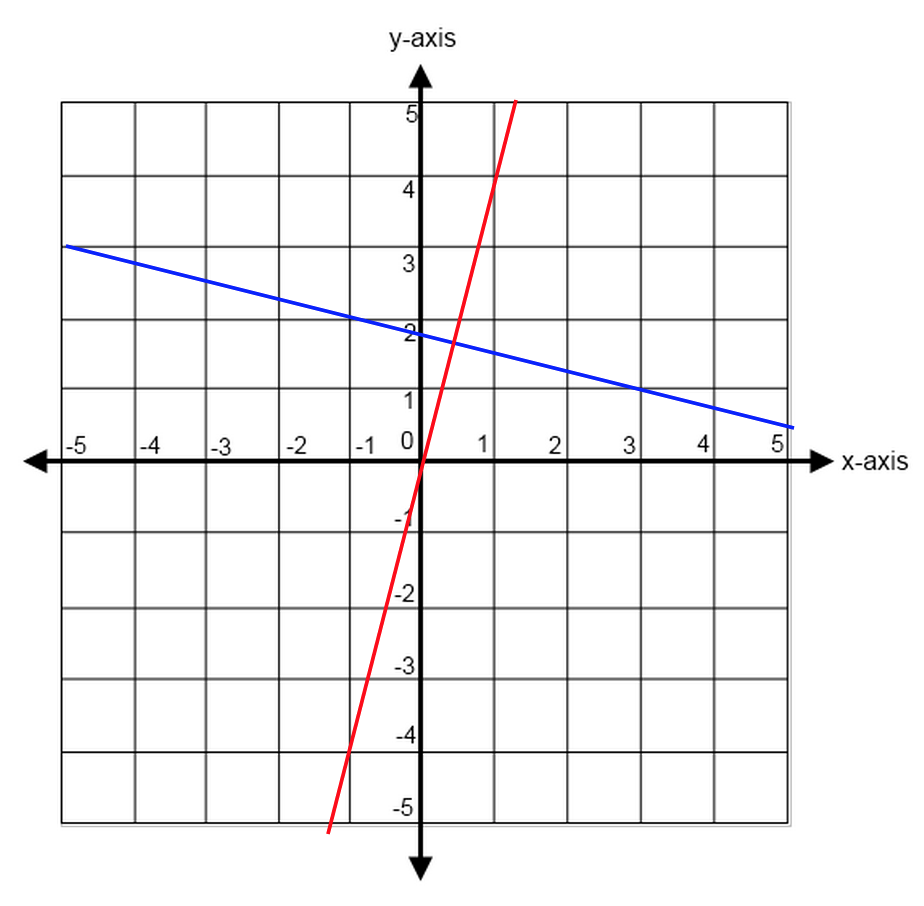
Parallel Lines
Two lines that will never meet (no matter how infinitely long they extend) are said to be parallel. This means that they are continuously equidistant from one another.
Parallel lines have the same slope. You can see why this makes sense, since the rise over run will always have to be the same in order to ensure that the lines will never touch.
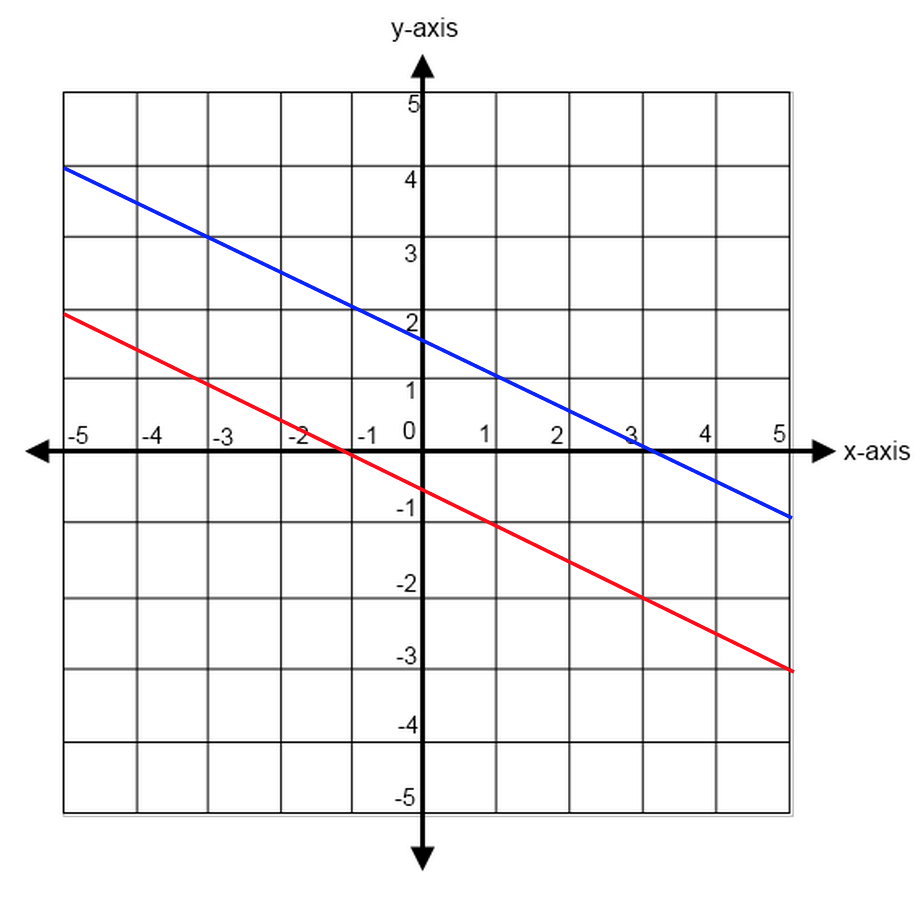
No matter how far they extend, these lines will never intersect.
What is the slope of any line parallel to the line $8x+9y=3$ in the standard $(x,y)$ coordinate plane?
F. -8
G. $-{8/9}$
H. $8/3$
J. 3
K. 8
First, let us re-write our equation into proper slope-intercept equation form.
$8x + 9y = 3$
$9y = -8x + 3$
$y = -{8/9} + 1/3$
Now, we can identify our slope as $-{8/9}$. We also know that parallel lines have identical slopes. So all lines parallel to this one will have the slope of $-{8/9}$.
Our final answer is G, $-{8/9}$.
 A...valiant attempt to be parallel.
A...valiant attempt to be parallel.
Typical Line and Slope Questions
Most line and slope questions on the ACT are quite basic at their core. You’ll generally see two to three questions on slopes per test and almost all of them will simply ask you to find the slope of a line when given coordinate points or intercepts.
The test may attempt to complicate the question by using other shapes or figures, but the questions always boil down to these simple concepts.
Just remember to re-write any given equations into the proper slope-intercept form and keep in mind your rules for finding slopes (as well as your rules for parallel or perpendicular lines), and you’ll be able to solve these types of problems easily.
What is the slope of the line through $(5,-2)$ and $(6,7)$ in the standard $(x,y)$ coordinate plane?
F. $9$
G. $5$
H. $-5$
J. $5/11$
K. $-{5/11}$
We have two sets of coordinates, which is all we need in order to find the slope of the line which connects them. So let us plug these coordinates into our slope equation:
${y_2 - y_1}/{x_2 - x_1}$
$(7 - 2)/(6 - -5)$
$5/11$
Our final answer is J, $5/11$

Despite the fact that we are now working with figures, the principle behind the problem remains the same--we are given a set of coordinate points and we must find their slope.
From C to D, we have coordinates (9, 4) and (12, 1). So let us plug these numbers into our slope formula:
${y_2 - y_1}/{x_2 - x_1}$
$(1 - 4)/(12 - 9)$
$-3/3$
$-1$
Our final answer is B, $-1$.
As you can see, there is not a lot of variation in ACT question on slopes. So long as you keep track of the coordinates you’ve assigned as $(x_1, y_1)$ and $(x_2, y_2)$, and you make sure to keep track of your negatives and positives, these questions should be fairly straightforward.
How to Solve a Line and Slope Problem
As you go through your line and slope problems, keep in mind these tips:
#1: Always rearrange your equation into $y = mx + b$
If you are given an equation of a line on the test, it will often be in improper form (for example: $10y + 15x = 20$).
If you are going too quickly through the test or if you forget to rearrange the given equation into proper slope-intercept form, you will misidentify the slope and/or the y-intercept of the line. So always remember to rearrange your equation into proper form as your first step.
$10y + 15x = 20$ => $y = -{3/2}x + 2$
#2: Remember your $\rise/\run$
Our brains are used to doing things "in order," so it can be easy to make a mistake and try to find the change in $x$ before finding the change in $y$. Keep careful track of your variables in order to reduce careless mistakes like this.
Remember the mantra of "rise over run" and this will help you always know to find your change in $y$ (vertical distance) over your change in $x$ (horizontal distance).
#3: Make your own graph and/or count to find your slope
Because the slope is always "rise over run," you can always find the slope with a graph, whether you are provided with one or if you have to make your own. This will help you better visualize the problem and avoid errors.
If you forget your formulas (or simply don't want to use them), simply draw your own graph and count how the line rises (or falls). Next, trace its "run." By doing this, you will always find your slope.

Now let's put your newfound knowledge to the test!
Test Your Knowledge
Now that we’ve walked through the typical slope questions you’ll see on the test (and the few basics you’ll need to solve them, let’s look at a few real ACT math examples:
1.
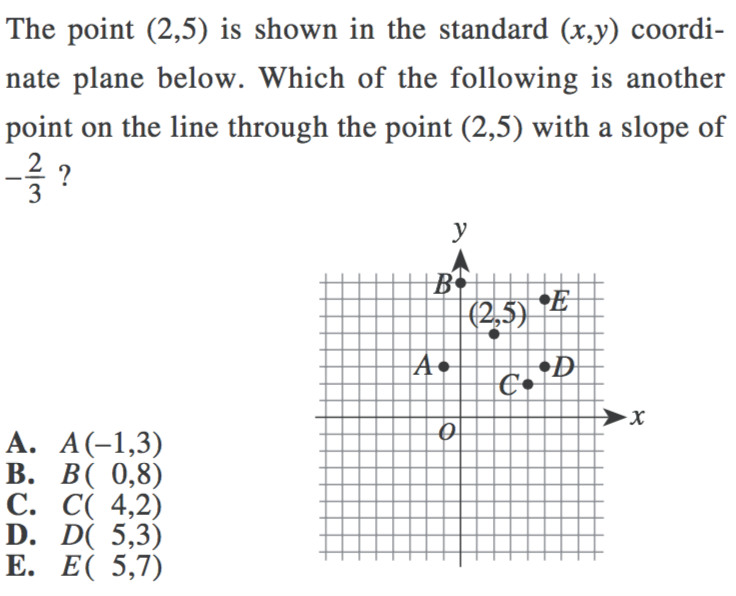
2.
Which of the following is the slope of a line parallel to the line $y={2/3}x-4$ in the standard $(x,y)$ coordinate plane?
A. $-4$
B. $-{3/2}$
C. $2$
D. $3/2$
E. $2/3$
3.
When graphed in the standard $(x,y)$ coordinate plane, the lines $x=-3$ and $y=x-3$ intersect at what point?
A. $(0,0)$
B. $(0,-3)$
C. $(-3,0)$
D. $(-3,-3)$
E. $(-3,-6)$
Answers: D, E, E
Answer Explanations:
1. You can solve this problem in one of two ways--by counting directly on the graph, or by solving for the changes in $x$ and $y$ algebraically. Let’s look at both methods.
Method 1—Graph Counting
The question was generous in that it provided us with a clearly marked graph. We also know that our slope is $-{2/3}$, which means that we must either move down 2 and over 3 to the right, or up 2 and over 3 to the left to keep our movement across a negative slope line consistent.
If you use this criteria to count along the graph, you will find that you hit no marked points by counting up 2 and over 3 to the left, but you will hit D when you go down 2 and over 3 to the right.
So our final answer is D.
Method 2—Algebra
Alternatively, you can always use your slope formula to find the missing coordinate points. If we start with our coordinate points of $(2, 5)$ and our slope of $-{2/3}$, we can find our next two coordinate points by counting finding the changes in our $x$ and $y$.
Our first coordinate point of $(2, 5)$ has a $y$ value of 5. We know, based on the slope of the line that the change in $y$ is +/- 2. So our next coordinate point must have a $y$ value of either:
$5 + 2 = 7$
Or
$5 - 2 = 3$
This means we can eliminate answer choices B and C.
Now we can do the same for our x-coordinate value.
We begin with $(2, 5)$, so our $x$ value is 2. Because the line has a slope of $-{2/3}$, our x-coordinate change at a rate of +/- 3. This means our next x-coordinate values must be either:
$2 + 3 = 5$
Or
$2 - 3 = -1$
Now, we must put this information together.
Because our slope is negative, it means that whatever change one coordinate undergoes, the other coordinate must undergo the opposite. So if we are adding the change in $y$, we must then subtract our change in $x$ (or vice versa).
This means that our coordinate points will either be $(5, 3)$ or $(-1, 7)$.
(Why? Because 5 comes from adding our change in $x$ and 3 comes from subtracting our change in $y$, and -1 comes from subtracting our change in $x$ and 7 comes from adding our change in $y$.)
The only coordinates that match are at D, $(5, 3)$.
Our final answer is D.
2. This question is simple so long as we remember that parallel lines have the same slopes and we know how to identify the slope of an equation of a line.
Our line is already written in proper slope-intercept form, so we can simply say that the line
$y = {2/3}x - 4$
has a slope of $2/3$, which means that any parallel line will also have a slope of $2/3$.
Our final answer is E, $2/3$
3. This question may seem confusing if you’ve never seen anything like it before. It is however, a combination of a simple replacement in addition to coordinate points.
We are given that $x = -3$ and $y = x - 3$, so let us replace our $x$ value in the second equation to find a numerical answer for $y$.
$y = x - 3$
$y = -3 - 3$
$y = -6$
Which means that the two lines will intersect at $(-3, -6)$.
Our final answer is E, $(-3, -6)$.

A good test deserves a good break, don't you think?
The Take-Aways
Though the ACT may present you with slightly different variations on questions about lines and slopes, these types of questions will always boil down to a few key concepts. Once you've gotten the hang of finding slopes, you'll be able to breeze through these questions in no time.
Make sure to keep track of your negatives and positives and remember your formulas, and you’ll be able to take on these kinds of questions with greater ease than ever before.
What’s Next?
Whew! You may know all you need to for ACT coordinate geometry, but there is so much more to learn! Check out our ACT Math tab to see all our individual guides to ACT math topics, including trigonometry, solid geometry, advanced integers, and more.
Think you might need a tutor? Take a look at how to find the right math tutor for your needs and budget.
Running out of time on ACT math? Check out how to buy yourself more time on ACT Math and complete your section within time.
Looking to get a perfect score? Our guide to getting a 36 on ACT math will help you iron out those problem areas and set you on the path to perfection.











