Most of us are familiar with the concept of rounding numbers. We round numbers all the time in our everyday lives, from telling time to taking measurements, since rounding is an easy and helpful way to help us make sense of the numbers around us. But what happens when we encounter decimals? Decimals can be long and unwieldy, and rounding can help make sense of them. Keep reading to find out how to round decimals, and how to use the common method of rounding.
What Is a Decimal?
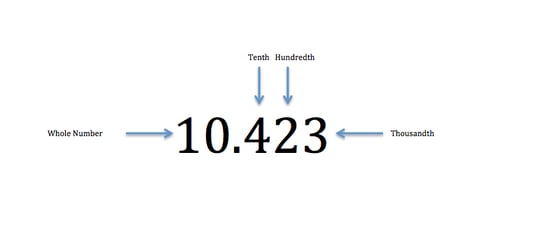
A decimal is a system of denoting integer and non-integer numbers that breaks down into tenths, hundredths, thousands, etc. The number is separated into a whole number, which is to the left of a decimal, and the fraction is to the right.
For example, let's look at the number 10.423. In this case, 4 is the tenth, 2 is the hundredth and 3 is the thousandth.
Decimals can be converted to fractions and percentages, which can make it easier to understand their value. Keep in mind that the placement of each number, where it appears after the decimal. So, if the number was 10.003 the number would be 10 and 3 thousandth, or 10 3/100. If the number was 10.03, it would be 10 3/100.
Using our number above, 10.423, we can break down the number:
.4= 4/10
.42= 42/100
.423= 423/100
When Will You Use Decimals?
Decimals are commonly used in our everyday lives, and you probably are capable of adding, subtracting, and rounding decimals in your head without even realizing you're doing it. We use decimals often when discussing money, weight, and measurements, since decimals can provide us with a precise value.
With that said, it's not always necessary to use a decimal in its entirety, whether in daily life or when solving a problem on a test. Though decimals can technically be infinite, we can utilize the common rounding method to round decimals, making them fit into the problem we're trying to solve.
Rounding Numbers: The Common Method
The common rounding method says that if the number you are rounding is followed by the number 5 or above (5,6,7,8,or 9) then you should round that number up. For example, you can round the number 27 to 30 because 7 is greater than 5. However, the number 24 would be rounded down to 20, because 4 is less than 5.
You can round to the nearest ten, as seen above, but you can also round to the nearest hundred or thousand. For example, 2,367 can be rounded to the nearest ten (2,370) the nearest hundred, (2,400) or the nearest thousand (2,000).
When rounding, you have to start with the number furthest to the right, since each number is used to round the number directly in front of it. In our example above, consider:
2,367 rounds up the 6
2,367 rounds up the 3
2, 367 rounds down to 2.

How to Round Decimals
Just like with whole numbers, we use the number directly to the right of each number to round. When rounding decimals, we also want to work our way back from the right.
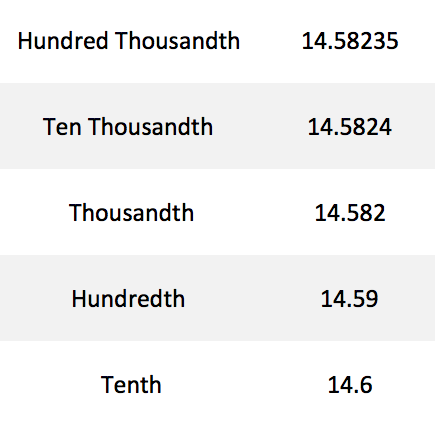
In our original example, 10.423, we know that we could quickly round down to 10, since all the numbers following the decimal are less than 5, and therefore all round down. So let's try a number that goes a little further out: 14.582354
This number can be rounded in many ways, depending on how precise you need it to be. At a certain point, the number past the decimal point is so small that it becomes inconsequential, depending on the situation. For example, if this were us weighing a cat, there's no need for us to know that the cat weighs 14.582354 pounds. We could safely round this number. However, if this was a scientific measurement of a certain chemical in a blood sample, the longer, more precise number is more useful to scientists, who need their measurements to be as accurate as possible. On the other hand, knowing our cat is about 14.6 pounds is more than enough information.
Here's what our number looks like rounding all the way to the tenth:
Knowing When You Should Round
Knowing when to round a decimal on a test is tough, and depends on what you're trying to solve for. Most tests will require a precise answer, which is why the decimal was included in the first place. If possible, try to stick with the original number. If rounding will help solve the problem more efficiently, stick at least to the hundredth. In a multiple choice situation, you can also look at how the answers are presented. If the answers go to the thousandth, you should do your calculations that way as well.
Though rounding can be tricky on tests, it's very useful for quick problem solving in everyday life. Say you're at the grocery store, and you're buying a watermelon. The watermelon is $0.35 per pound. You weigh your watermelon and it's 20.824 pounds. You can quickly round up both the pounds and the price, so you can multiply 21 x 0.40 and get a rough idea of how much you'll pay for the watermelon. Remember, the more you round the less precise the number gets, but this allows you to quickly get an idea of the price.
We don't need an exact number for the price of our watermelon, but if we were building a desk, for example, it's very important to measure out exactly the right measurement for each leg of the desk. In this situation, there's a big difference between 22.7 inches and 22.9 inches.
Always make sure to evaluate how precise you need a number to be before rounding it. Most of us can round up and down in our heads, but always be sure to use the common method of rounding in both everyday and test-taking situations.
What's Next?
Need more about decimals, fractions, and percentages? Check out The 3 Steps to Convert Decimals to Fractions (and Back)
Looking for the best math test-taking strategies? Get started with this review of What's Tested On the SAT Math Section, and make sure you check out PrepScholar's Ultimate Math SAT Prep Guide to conquer the SAT math section.