
Trigonometry and radians are important parts of the digital SAT Math section! Do you love SOHCAHTOA and ${π}$ angle measurements? Do you hate trigonometry and radians and don't know what SOHCAHTOA or ${π}/{2}$ means?
No matter how you feel about SAT trigonometry, there is no need to stress. In this guide, I'll let you know everything you need to know about trigonometry and radians for the SAT Math test and guide you through some practice problems.
Trigonometric Formulas: Sine, Cosine, Tangent
With the launch of the new digital SAT, trigonometry is a more important part of SAT Math than ever. Together, geometry and trig questions make up 15% of all SAT Math questions, more than double what it was before. So you'll want to get those questions right, and you won't be able to answer any trigonometry questions correctly without knowing the following formulas:
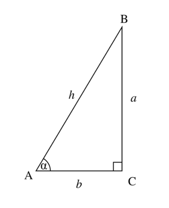
Find the sine of an angle given the measures of the sides of the triangle.
$$\sin(x)={\(Measure\: of\: the\: opposite\: side\: to\: the\: angle)}/{\(Measure\: of\: the\: hypotenuse)}$$
In the figure above, the sine of the labeled angle would be ${a}/{h}$
Find the cosine of an angle given the measures of the sides of the triangle.
$$\cos(x)={\(Measure\: of\: the\: adjacent\: side\: to\: the\: angle)}/{\(Measure\: of\: the\: hypotenuse)}$$
In the figure above, the cosine of the labeled angle would be ${b}/{h}$.
Find the tangent of an angle given the measures of the sides of the triangle.
$$\tan(x)={\(Measure\: of\: the\: opposite\: side\: to\: the\: angle)}/{\(Measure\: of\: the\: adjacent\: side\: to\: the\: angle)}$$
In the figure above, the tangent of the labeled angle would be ${a}/{b}$.
A helpful memory trick is an acronym: SOHCAHTOA.
Sine equals Opposite over Hypotenuse
Cosine equals Adjacent over Hypotenuse
Tangent equals Opposite over Adjacent
You should also know the complementary angle relationship for sine and cosine, which is $\sin(x°)=\cos(90°−x°)$.
How to Apply Trigonometry Skills on SAT Math
There are two main trigonometry questions types you'll see on the test. I'll teach you how to address each.
Question type 1 will ask you to find the sine, cosine, or tangent and using the measures of the sides of the triangle. In order to answer these questions, you will need to use a diagram (that means drawing one if it's not given to you). Let's walk through this example:
Triangle ABC is a right triangle where angle B measures 90°; the hypotenuse is 5 and side AB is 4. What is cosine A?
First, set up this triangle using the given information:

Then, identify the information you need. In this case, the question asked for the cosine A. We know, based on the previous formulas that $\cos(A)={\(Measure\: of\: the\: adjacent\: side\: to\: the\: angle)}/{\(Measure\: of\: the\: hypotenuse)}$. Identify the pieces you need: the angle, the adjacent side to the angle, and the hypotenuse:
 We have all the information we need, so we just need to put it into the formula:
We have all the information we need, so we just need to put it into the formula:
$\cos(A)={\(Measure\: of\: the\: adjacent\: side\: to\: the\: angle)}/{\(Measure\: of\: the\: hypotenuse)}={4}/{5}$.
${4}/{5}$ is the answer.
A slightly harder version of this question might ask you for sine A instead of cosine A. If you look back at the diagram, you'll notice we don't know what the measure of the opposite side to angle A is (which is what we need to find sine A).

In that case, we need to use the Pythagorean theorem (or our knowledge of 3-4-5 right triangles) to find the measure of the opposite side to angle A (BC).
$$BC=√{(5^2)-(4^2)}=√{(25)-(16)}=√{9}=3$$
Know that we know that side BC is 3, we just need to put it into the formula:
$$\sin(A)={\(Measure\: of\: the\: opposite\: side\: to\: the\: angle)}/{\(Measure\: of\: the\: hypotenuse)}={3}/{5}$$
Question type 2 will ask you to find the sine, cosine, or tangent of an angle using a different given sine, cosine, or tangent of an angle. Similarly to question type one, to answer these questions, you'll need to use a diagram (that means drawing one if it's not given to you). Check out this example:
In a right ABC triangle, where B is the right angle, $\cos(A)={4}/{5}$. What is the sin(C)?
You want to attack these problems by drawing a diagram, but first you need to figure out what should go where. Use the cosine formula to figure out how to draw the diagram.
$$\cos(A)={\(Measure\: of\: the\: adjacent\: side\: to\: the\: angle)}/{\(Measure\: of\: the\: hypotenuse)}={4}/{5}$$
Measure of adjacent side (AB) = 4
Measure of the hypotenuse (AC) = 5

You may notice it's the same triangle from the previous example. In this case, we want to find cosine C. We know, based on the previous formulas that $\sin(C)={Measure\: of\: the\: opposite\: side\: to\: the\: angle}/{Measure\: of\: the\: hypotenuse}$. Identify the pieces you need: the angle, the adjacent side to the angle, and the hypotenuse.
$$\sin(C)={\(Measure\: of\: the\: opposite\: side\: to\: the\: angle)}/{\(Measure\: of\: the\: hypotenuse)}={4}/{5}$$
${4}/{5}$ is the answer.
A slightly harder version of this question might ask you for tangent C instead of sine C. If you look back at the diagram, you'll notice we don't know what the measure of the adjacent side to angle C is (which is what we need to find tan A).

In that case, we need to use the Pythagorean theorem (or our knowledge of 3-4-5 right triangles) to find the measure of the adjacent side to angle C (BC).
$$BC=√{(5^2)-(4^2)}=√{(25)-(16)}=√{9}=3$$
Know that we know that side BC is 3, we just need to put it into the formula:
$$\tan(C)={\(Measure\: of\: the\: opposite\: side\: to\: the\: angle)}/{\(Measure\: of\: the\: adjacent\: side\: to\: the\: angle)}={4}/{3}$$
Now that we know how to apply the necessary formulas to tackle trig questions, let's try to apply them to some real SAT practice problems.
SAT Trigonometry Practice Problems
Example #1

Answer Explanation: Triangle ABC is a right triangle with its right angle at B. Therefore, AC is the hypotenuse of right triangle ABC, and AB and BC are the legs of right triangle ABC. According to the Pythagorean theorem,
$$AB=√(202)−(162)=√(400)−(256)=√144=12$$
Since triangle DEF is similar to triangle ABC, with vertex F corresponding to vertex C, the measure of angle F equals the measure of angle C. Therefore, $\sinF=\sinC$. From the side lengths of triangle ABC, $\sin C={\(Measure\: of\: the\: opposite\: side\: to\: the\: angle)}/{\(Measure\: of\: the\: hypotenuse)}={\AB}/{\AC}={12}/{20}={3}/{5}$. Therefore, $\sinF={3}/{5}$.
The final answer is ${3}/{5}$ or .6.
Example #2

Answer Explanation: There are two ways to solve this. The quicker way is if you know the complementary angle relationship for sine and cosine, which is $\sin(x°)=\cos(90°−x°)$. Therefore, $\cos(90°−x°)={4}/{5}$ or 0.8.
However, you can also solve this problem by constructing a diagram using the given information. It's a right triangle (which it has to be to use sine/cosine), and the sine of angle x is ${4}/{5}$ if $\sine={\(opposite\: side)}/{\hypotenuse}$ then the opposite side is 4 long, and the hypotenuse is 5 long:

Since two of the angles of the triangle are of measure x° and 90°, the third angle must have the measure $180°−90°−x°=90°−x°$. From the figure, $\cos(90°−x°)$, which is equal the ${adjacent\: side}/{the\: hypotenuse}$, is also ${4}/{5}$ or 0.8.
Example #3

Answer Explanation: Similarly to the other trigonometry problem, there are two ways to solve this problem.
The quicker way is to realize that x and y are complementary angles (add up to 90°). Then, using the complementary angle relationship for sine and cosine, which is $\sin(x°)=\cos(90°−x°)$, you realize that $\cos(y°)=0.6$.
However, you can also solve this problem by constructing a diagram using the given information. It's a right triangle (which it has to be to use sine/cosine), and the sine of angle x is 0.6. Therefore, the ratio of the side opposite the x° angle to the hypotenuse is .6.
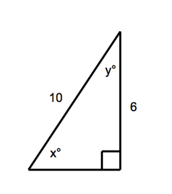
The side opposite the x° angle is the side adjacent to the y° angle. $\cos(y°)={\(the\: side\: adjacent\: to\: the\: y°\: angle)}/{\(the\: hypotenuse)}={6}/{10}$, is equal to .6.
The answer is 0.6.
Radians
Radians will only account for a small portion (around 5%) of SAT math questions, but you still want to get those questions right! Radians are one of the trickier concepts. What do you need to know about radian measure?
Definition of Radian Measure
The bare bones definition: Radian is a measure of an angle (just as degree is a measure of angle).
The in-depth/conceptual version: Radian is a measure of an angle that is based on the length of the arc that the angle intercepts on the unit circle. That sounds like gibberish I know. Let me break it down. A unit circle is a circle with a radius of 1 unit. See picture:

Gustavb/Wikimedia
The circumference (or length around) this unit circle is ${2π}$, since ${C=2πr}$, and r=1.
If the measure of an angle were 360°, the radian measure would be ${2π}$ since the length of the arc that the 360° angle intercepts on the unit circle would be the whole circumference of the circle (which we already established was ${2π}$). Here are some good basic radian measures to have memorized:
|
Degrees
|
Radians
(exact)
|
|
30°
|
${π}/{6}$
|
|
45°
|
${π}/{4}$
|
|
60°
|
${π}/{3}$
|
|
90°
|
${π}/{2}$
|
How to Convert Between Angle Measure in Degrees and Radians
To go from degrees to radians, you need to multiply by ${π}$, divide by 180°. Here is how to convert 90° to radians:
$${90°π}/{180°}$$
$$={π}/{2}$$
To go from radians to degrees, you need to multiply by 180°, divide by ${π}$. Here is how to convert ${π}/{4}$ to degrees:
$${({π}/{4})(180°)}/{π}$$
$$={({180°π}/{4})/{π}$$
$$=45°$$
How to Evaluate Trigonometric Functions at Benchmark Angle Measures
The benchmark angle measures (as defined by the College Board) are 0, ${π}/{6}$, ${π}/{4}$, ${π}/{3}$, ${π}/{2}$ radians which are equal to the angle measures 0°, 30°, 45°, 60°, and 90°, respectively.
You need to be able to use these with the trigonometric functions described in the above trigonometry section (sine, cosine, and tangent). You will not be asked for values of trigonometric functions that require a calculator.
Remember, the complementary angle relationship for sine and cosine, which is $\sin(x°)=\cos(90°−x°)$ will be $\sin(x)=\cos({π}/{2}−x)$ when converted into radians.
SAT Radians Practice Problems
Example #1
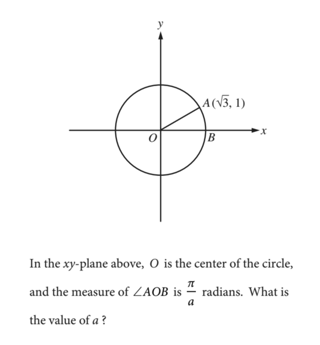
Answer Explanation: The correct answer is 6. By the distance formula, the length of radius OA is $√{((√3)^2)+(1^2)}=√{3+1}=√{4}=2$. Thus, $\sin(∠AOB)={1}/{2}$.
Therefore ∠AOB is 30°, which is equal to $30({π}/{180})={π}/{6}$ radians. Hence, the value of a is 6.
Example #2

Answer Explanation: A complete rotation around a point is 360° or ${2π}$ radians. Since the central angle AOB has measure ${5π}/{4}$ radians, it represents $/{2π}={5}/{8}$ of a complete rotation around point O. Therefore, the sector formed by central angle AOB has area equal to ${5}/{8}$ the area of the entire circle. The answer is ${5}/{8}$ or in decimal form .625.
Example #3
Which of the following is equivalent to $\cos({3π}/{10})$?
A) $\-cos ({π}/{5})$
B) $\sin ({7π}/{10})$
C) $\-sin ({π}/{5})$
D) $\sin ({π}/{5})$
Answer Explanation: To answer this question correctly, you need to both understand trigonometry and radians. Sine and cosine are related by the equation $\sin(x)=\cos({π}/{2}-x)$.
In order to find out what the equivalent to $\cos({3π}/{10})$ is, you need to change ${3π}/{10}$ into the form ${π}/{2}-x$. To do that, you need to set up an equation:
$${3π}/{10}= {π}/{2}-x$$
Then, solve for x.
$${3π}/{10}-{π}/{2}=-x$$
$${3π}/{10}-{5π}/{10}=-x$$
$$-{2π}/{10}=-x$$
$${2π}/{10}=x$$
$${π}/{5}=x$$
Therefore, $\cos({3π}/{10})=\cos({π}/{2}-{π}/{5})=\sin({π}/{5})$. D is the correct answer.
Test Yourself on SAT Trigonometry Questions!
Practice #1
In triangle DCE, the measure of angle C is 90°, $\DC=5$ and $\CE=12$. What is the value of $\sin(D)$?
Practice #2
In a right triangle, $\cos({π}/{2}-x)={6}/{8}$. What is $\sin(x)$?
Practice #3
In circle O, central angle AOB has a measure of ${3π}/{4}$ radians. The area of the sector formed by central angle AOB is what fraction of the area of the circle?
Answers: #1: ${12}/{13}$, #2: ${6}/{8}$, 3) ${3}/{8}$
What's Next?
Now that you know how to handle trigonometry and radians, make sure you're prepared for all of the other math topics you'll see on the SAT. All of our math guides will take you through strategies and practice problems for all the topics covered on the math section, from integers to ratios, circles to polygons (and more!).
Feeling anxious about test day? Make sure you know exactly what to do and bring to ease your mind and settle your nerves before it's time to take your SAT.
Running out of time on the SAT math section? Look no further than our guide to help you beat the clock and maximize your SAT math score.
Angling to get a perfect score? Check out our guide to getting a perfect 800, written by a perfect-scorer.












