Though triangles are far and away the most common geometric shape on the SAT, make sure not to underestimate the importance of circles. You will generally come across 2-3 questions on circles on any given SAT, so it’s definitely in your best interest to understand the ins and outs of how they work. And this guide is here to show you the way.
This will be your complete guide to SAT circles, including areas, circumferences, degrees, arcs, and points on a circle. We’ll take you through what these terms mean, how to manipulate and solve for various aspects of a circle, and how to tackle the most difficult SAT circle questions you may see on test day.
What Are Circles?
A circle is a two dimensional shape that is formed from the infinite number of points equidistant (the same distance) from a single point. This single point becomes the center of the circle.
This means that any and all straight lines drawn from the circle’s center will exactly hit the edge of the circle, so long as all the lines are of equal length.
Degrees
Though you can measure a circle in both degrees and radians, you will only ever have to use degrees on the SAT. Because of this, we will only be talking about degree measures in this guide.

A full circle has 360 degrees. A semicircle (half a circle) has $360/2 = 180$ degrees. This is why a straight line always measures 180 degrees.
To find a piece of a circle, you must find it in relation to 360 degrees. So a fifth of a circle is $360(1/5) = 72$ degrees, and an eighth of a circle is $360(1/8) = 45$ degrees, etc.
Circumference
The circumference is the edge of the circle. It is made from the infinite points equidistant from the center.
In formulas, the circumference is represented as $c$.
Diameter
A diameter is any straight line drawn through the center of the circle that connects two opposite points on the circumference.
In formulas, the diameter is represented as $d$.
Radius
The radius of a circle is a straight line drawn from the center of the circle to any point on the circumference. It is always half the diameter.
In formulas, the radius is represented as $r$.

Tangency
Circles are described as “tangent” with one another when they touch at exactly one point on each circumference.

A group of circles, all tangent to one another.
π (pi)
If you’ve taken a geometry class, then you are also probably familiar with π (pi). π is the mathematical symbol that represents the ratio of any circle’s circumference to its diameter. It is usually expressed as 3.14(159), but its digits go on infinitely. (For more information on ratios, check out our guide to SAT ratios.)

Let's say we have a circle with a particular diameter (any diameter). Now let's multiply this same circle a few times and line them all up in a row. This gives us our same diameter 4 times in a line.

Now, let us assign a starting point somewhere on the circumference of the circle and then "unpeel" the circumference from our circle.

Once you remove the circumference and lay it flat, you can see that the circumference is a little more than 3 full lengths of the circle's width/diameter (specifically, 3.14159 times).

The circumference of the circle will always be 3.14159 (π) times the diameter. So, if a circle’s diameter is 1, then its circumference is π. And if its diameter is 2, then its circumference is 2π, etc.

We can measure all the distance ever traveled (with wheels) in increments of pi.
Circle Formulas
You will always be given a box of formulas on each SAT math section. This means it is not crucial for you to memorize circle formulas, but we still recommend that you do so if possible. Why? To help both your time management and problem solving ability.

The box of formulas you'll be given on every SAT math section.
In terms of time management, memorizing your formulas will save you time from pulling up the formula sheet over and over again, which takes your attention away from the question you’re working on. And, on a timed standardized test like the SAT, every second counts.
It is also in your best interest to memorize your formulas simply for ease, practice, and familiarity. The more comfortable you get in knowing how circles work, the more quickly and easily you’ll be able to solve your problems.
So let’s look at your formulas.
Circumference
$$c = πd$$
$$c = 2πr$$
There are technically two formulas to find the circumference of a circle, but they mean exactly the same thing. (Why? Because any diameter will always be equal to twice the circle’s radius).
Because π is the relationship between a circle’s diameter and its circumference, you can always find a circle’s circumference as long as you know its diameter (or its radius) with these formulas.

Here, we have two half circles and the sum of two radii, $RS = 12$.
We can either assign different values for the radius of circle R and the radius of circle S such that their sum is 12, or we can just mentally mash the two circles together and imagine that RS is actually the diameter of one circle. Let’s look at both methods.
Method 1
Since we know that $RS = 12$, let us say that circle R has a radius of 4 and circle S has a radius of 8. (Why those numbers? Because all that matters is that the radii add up to equal 12. We could have picked 6 and 6, 10 and 2, 3 and 9, etc., so long as their sum was 12.)
So the circumference of circle R would be:
$c = 2πr$
$c = 2π4$
$c = 8π$
But, since we only have half a circle, we must divide that number in half.
${8π}/2 = 4π$
$c = 4π$
Now, we can do the same for circle S. But we can also see that it is a semi-circle. So instead of taking our circumference of $2πr$ for the whole circumference, let us just take the circumference of half ($πr$) and so save ourselves the trouble of all the steps we used for circle R.
${1/2}c = πr$
${1/2}c = 8π$
So now let us add our circumferences.
$4π + 8π = 12π$
So our final answer is C, $12π$
Method 2
On the other hand, we could simply imagine that line RS is the diameter of a complete circle. (Why are we allowed to do this? Because we have the sum of two radii and two half circles, so combined, they would become one circle.)
If RS is a diameter of a circle whose complete circumference we must find, let us use our circumference formula.
$c = πd$ or $c = 2πr$
$c = 12π$
Again, our answer is C, $12π$.
Area
$$a = πr^2$$
You can also use π to find the area of a circle as well, since a circle’s area is closely related to its circumference. (Why? A circle is made of infinite points, and so it is essentially made up of infinite triangular wedges--basically a pie with an infinite number of slices. The height of each of these wedges would be the circle’s radius and the cumulative bases would be the circle’s circumference.)
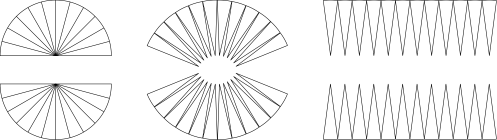
A circle splitting into a series of triangles.
So you would be able to find a circle’s area using the formula:
$a = πr^2$
Arcs
$$c \arc = πd({\arc \degree}/360°)$$
$$a \arc \sector = πr^2({\arc \degree}/360°)$$
In order to find the circumference of a circle’s arc (or the area of a wedge made from a particular arc), you must multiply your standard circle formulas by the fraction of the circle that the arc spans.
To determine the fraction of the circle that the arc spans, you must have the degree measure of the arc and find its measure out of the circle’s full 360 degrees. So if you want to find the circumference of an arc that is 90°, it would be $1/4$ the total area of the circle. Why? Because $360/90 = 4$ (in other words, $90/360 = 1/4$).

This question gives us a lot of information, so let’s go through it piece by piece.
First of all, we are trying to find the length of an arc circumference, which means that we need two pieces of information--the arc degree measure and the radius (or the diameter).
Well, we have the degree measure, so we’re halfway there, but now we need the radius (or diameter) of the smaller circle. We are told that it is half the radius of the larger circle, so we must find the radius of the larger circle first.
All that we are told about the larger circle is that it has a circumference of 36. Luckily, we can find its radius from its circumference.
$c = 2πr$
$36 = 2πr$
$18 = πr$
$18/π = r$
[Note: though it is unusual, this problem gives us our radius in pi units, rather than giving our circumference(s) in pi units. As we said, this is perfectly acceptable, though uncommon.]
If the circumference of the larger circle is 36, then its diameter equals $36/π$, which means that its radius equals $18/π$.
Because we know that the smaller circle has a radius that is half the length of the radius of the larger circle, we know that the radius of the smaller circle is:
$({18/π})/2 = 9/π$
So the radius of our smaller circle is $9/π$. This means we can finally find the arc measure of the smaller circle’s circumference, by using the radius of the circle and the interior degree measure.
$c_\arc = 2πr({\arc \degree}/360)$
$c_\arc = 2π({9/π})(80/360)$
$c_\arc = 4$
So our final answer is D, 4.

The relationship between circles and pi is constant and unbreakable.
Typical Circle Questions on the SAT
Circle problems on the SAT will almost always involve a diagram. With very rare exceptions, you will be given a picture from which to work. But we will discuss both diagram and word problems here on the chance that you will get multiple types of circle problems on your test.
Diagram Problem
A diagram problem will give you a diagram from which to work. You must use the visual you are provided and either find a missing piece or find equivalent measurements or differences.
Helpful hint: often (though not always), the trick to solving a circle problem is in finding and understanding the radius. All lines drawn from the center of the circle to the circumference are radii, and are therefore equal. This will often play a vital part to solving the whole problem.

Here is a perfect example of when the radius makes all the difference in a problem.
We are told that lines AB and AO are equal. Based on our knowledge of circles, we also know that AO and BO are equal. Why? Because they are both radii, and the radii of a circle are always equal.
This means that AB = AO = BO, which means that the triangle is equilateral.
Equilateral triangles have all equal sides and all equal angles, so the measure of all its interior angles are 60°. (For more on equilateral triangles, check out our guide to SAT triangles)
So angle measure ABO = 60 degrees.
Our final answer is D.
Word Problem
Word problem questions about circles will describe a scene or situation that revolves around circles in some way.
Generally, the reason why you will not be given a diagram on a circle question is because you are tasked with visualizing different types of circle types or scenarios. On rare occasions, you may get a word problem on circles because the question describes an inequality, which is difficult to show in a diagram.
When given a word problem question, it is a good idea to do your own quick sketch of the scene. This will help you keep all the details in order and/or see if you can make multiple types of shapes and scenarios, as with this question:

Here, we are being asked to visualize several potential different shapes and outcomes of this circle, which is why this problem is presented to us as a word problem. Because there are many different ways to draw out this scenario, let us look to the answer choices and either eliminate them or accept them as we go along.
Option I considers the possibility that M could be the center of the circle if lines XM and YM are equal and X and Y both lie somewhere on the circumference of the circle. We know this must be true because M being the center point of the circle would make lines XM and YM radii of the circle, which would mean that they were equal.

So option I is true and we can therefore eliminate answer choices B and D.
Now let’s look at option II.
Option II presents us with the possibility that point M lies somewhere on the arc of XY. Well, if point M rested exactly halfway between X and Y, then straight lines drawn from X to M and Y to M would certainly be equal.

So option II is also correct.
Finally, let’s look at option III.
Option III presents us with the possibility that M lies somewhere on the outside of the circle. So long as M lies at a distance halfway between X and Y, this scenario would still work.

So option III is also correct.
This means that all of our options (I, II, and III) are possible.
Our final answer is E.

Now let's talk circle tips and tricks.
How to Solve a Circle Problem
Now that you know your formulas, let’s walk through the SAT math tips and strategies for solving any circle problem that comes your way.
#1: Remember your formulas and/or know where to look for them
As we mentioned earlier, it is always best to remember your formulas when you can. But if you don’t feel comfortable memorizing formulas or you fear you will mix them up, don’t hesitate to look to your formula box--that is exactly why it is there.
Just be sure to look over the formula box before test day so that you know exactly what is on it, where to find it, and how you can use that information. (For more on the formulas you are given on the test, check out our guide to SAT math formulas.)
#2: Draw, draw, draw
If you’re not given a diagram, draw one yourself! It doesn’t take long to make your own picture and doing so can save you a lot of grief and struggle as you go through your test. It can be all too easy to make an assumption or mix up your numbers when you try to perform math in your head, so don’t be afraid to take a moment to draw your own pictures.
In Bluebook, you won’t be able to mark up diagrams in the actual exam. But the digital SAT features an online notepad that you can use to reproduce and mark up diagrams that are provided on exam questions. Alternatively, you can bring a pen or pencil, and the proctor will provide paper if you ask for it. The reason not everything is marked in your diagrams is so that the question won’t be too easy, so always write in your information yourself.
#3: Analyze what’s really being asked of you
All the formulas in the world won’t help you if you think you’re supposed to find the area, but you’re really being asked to find the circumference. Always remember that standardized tests are trying to get you to solve questions in ways in which you’re likely unfamiliar, so read carefully and pay close attention to the question you’re actually being asked.
#4: Use your formulas
Once you’ve verified what you’re supposed to find, most circle questions are fairly straightforward. Plug your givens into your formulas, isolate your missing information, and solve. Voila!
Test Your Knowledge
Now let's put your newfound circle knowledge to the test on some real SAT math problems.
1)

2)

3)

Answers: C, D, C
Answer Explanations:
1) This question involves a dash of creativity and is a perfect example of a time when you can and should draw on your given diagrams (had you been presented this on paper, that is).
We know that the inscribed figure is a square, which means that all of its sides are equal (for more on squares, check out our guide to SAT polygons). Therefore, if you draw a line connecting points R and T, you will have a perfect semi-circle, or 180°.

Now, the arc we are looking for spans exactly half of that semi-circle.

This means that the arc degree measure of ST is:
$180/2 = 90$ degrees.
So our final answer C.
2) Now, before we even begin, read the question carefully. The question wants us to find the perimeter of the shaded region. If you were going too quickly through the test, you may have been tempted to find the area of the shaded region instead, which would have gotten you a completely different answer.
Because we are trying to find the perimeter of circular figures, we must use our formula for circumferences.
Let us start with the two circles in the middle.
We know that each circle has a radius of 3 and that our shaded perimeter spans exactly half of each circle. So the circumference for each small circle is:
${1/2}c = πr$
$c = 3π$
And there are two small circles, so we must double this number:
$3π * 2 = 6π$
So the interior perimeter is $6π$.
Now, let’s find the outer perimeter, which is the circumference for half the larger circle.
If the radius of each of the small circles is 3, then that means the diameter of each small circle is:
$3 * 2 = 6$
And the diameter of each small circle is the same as the radius of the larger circle. This means that the full circumference of the larger circle is:
$c = 2πr$
$c = 2π6$
$c = 12π$
But we know that our perimeter only spans half the outer circumference, so we must divide this number in half.
${12π}/2 = 6π$
Our outer perimeter equals $6π$ and our inner perimeter equals $6π$. To get the full perimeter, we must add them together.
$6π + 6π = 12π$
Our final answer is D, $12π$.
3) Here, we are beginning with the understanding that the circle has an area of $25π$. We are tasked with finding the perimeter of one of the wedges, which requires us to know the radius length of the circle. This means we must work backwards from the circle’s area in order to find its radius.
Well the formula for the area of a circle is:
$a = πr^2$
Our area equals 25, so:
$√25 = 5$
Our radius measurement equals 5.
Now, we must find the arc measurement of each wedge. To do so, let us find the full circumference measurement and divide by the number of wedges (in this case, 8).
$c = 2πr$
$c = 2π5$
$c = 10π$
The full circumference is $10π$ which, divided by 8, is:
${10π}/8 = {5/4}π$
Now, let us add that arc measurement to twice the radius value of the circle in order to get the full perimeter of one of the wedges.
$5 + 5 + {5/4}π$
$10 + {5/4}π$
So our final answer is C.

The Take-Aways
Almost always, the most useful part of any circle will be the radius. Once you’ve gotten used to thinking that all radii are equal, then you will often be able to breeze past even the trickiest of SAT circle problems.
If you understand how radii work, and know your way around both a circle’s area and its circumference, then you will be well prepared for most any circle problem the SAT can dream up. Know that the SAT will present you with problems in strange ways, so remember your tricks and strategies for circle problems. Be careful with your work, keep a clear head, and you’ll do just fine.
What’s Next?
You've triumphed over circles (huzzah!). So now what? Well we've got guides aplenty on any SAT math topic you want to brush up on. Feel iffy on your lines and angles? How about probability? Integers? Check out our SAT math tab on the blog for any SAT math topic questions you might have.
Don't know where to start? First, make sure you understand how the test is scored and what makes a "good" score or a "bad" score, so that you can figure out how you currently stack up.
Want to get a 600 on the SAT math? How about a perfect 800? Check out our articles on how to bring your scores up to a 600 and even how to get a perfect score on the SAT math, written by a perfect SAT-scorer.