In a way, single variable equations are some of the most common and least common types of questions on the SAT math section. Why? Because it’s rare to find more than one or two single variable equations per test, and yet knowing how to solve and manipulate single variable equations is a basic requirement for solving most all SAT math questions.
Even though you won’t often see single variable equations by themselves, it is crucial that you know how to set up, use, and manipulate them. You cannot solve the more complex expressions like quadratics, multiple variables, and so on, without first understanding single variable equations.
This guide will be your complete walk-through of single variable equations for the SAT--what they are, how you’ll see them on the test, and how to set up and solve them.
Once you get the hang of single variable equations, you can go on to solve more and more complex problems.
What Are Single Variable Equations?
A single variable equation is comprised of two parts: the (lone) variable and the equation. So let’s look at what those are and how to put them together.
A variable is a symbolic placeholder for a number we do not yet know. Often, you’ll see x or y used as a variable in math problems, but variables can be represented by any symbol or letter.
$$4t=20$$
In this case, t is our variable. It represents a number that is currently unknown.
An equation sets two (or more) mathematical expressions equal to one another. To show that the expressions are equal, we use an equals sign (=).
Each side of the expression can be as simple as a single integer or as complex as an expression with multiple variables, exponents, or anything else.
$$15(a+b^3)−(a−3)^12=22$$
The above is an example of an equation. Each side of the expression equals the other.
So if we put together our definitions, we know that:
A single variable equation is an equation in which there is only one variable. The variable can be used multiple times and/or used on either side of the equation as long as the variable remains the same.
Some examples of single variable equations:
$${4(a−3)}/a=2(a^8)$$
$$a+7−(a+3)=4$$
$$6a+a−3=a+21$$
You’ll notice that some of the equations used the variable, a, multiple times. Other equations used the variable on either side of the equals sign.
No matter how many times the variable is used, all of these are still single variable problems because the variable remains constant and there are no other variables.
Once you find your variable, you can solve the whole puzzle.
Typical Single Variable Equations on the SAT
Single variable equations will fall into two broad categories on the SAT--given equations and word problems. Word problems are by far the more common and you should expect to see one or two per test. Given equations, when they appear, will usually fall between problems 1-4 on any given math section.
Let’s look at each type.
Given Equations
A given equation will provide you with the equation you need to use to solve the problem. We will go through the exact processes needed to solve this kind of problem in the next section, but for now just understand that your goal is to isolate your variable.
(We will walk through how to solve this question later in the guide)
In this problem, you are being asked to find the isolated variable as your final answer. But do be sure to note that this is not always the case.
Sometimes the question will ask you to solve for y alone (or x or any other variable), and sometimes the question will ask you to solve for y to a different term (2y or 12y, etc.).
Always pay close attention to exactly what the question is asking you to find. You need to first isolate your variable to solve the problem, but always double-check whether you should stop there or if you need to continue on, in order to find your final answer.
Word Problems
A word problem will describe a situation and ask you to find a missing variable. You must write your own equation based on the information you are given in the question.
Again, your final answer may be the value of your variable (x or y, etc.) or your variable taken to a different term ($2x$, $y^2$, etc.).
(We will walk through how to solve this question later in the guide)
How to Manipulate a Single Variable Equation
In order to solve a single variable equation, we must isolate our variable on one side of the equation. And the way we do this is by shifting everything else to the other side of the equals sign.
In order to shift our terms (expressions), we must cancel them out on their original side. This means we have to set the non-variables to zero when using addition/multiplication, and set the variable to 1 when using division/multiplication.
(Why do we set it to 1 when using division/multiplication? Because we use multiplication and division to isolate our variable. But setting it to 1, we give ourselves just the one variable to work with.)
The way we cancel out our terms is by performing the opposite function of each term. Opposite function pairs are:
- Addition and subtraction
- Multiplication and division
For example, if we have a term on one side that has a minus sign (subtraction), we must add that same amount from both sides.
$x−4=6$
$x−4+4=6+4$
$x=10$
If we have a term that is being multiplied, we must divide that same amount from both sides.
$4x=20$
${4x}/4={20}/4$
$x=5$
And so on.
Whatever you do on one side of the equation, you must do on the other. This cancels out like terms and essentially moves your terms from one side of the equation to the other.
Manipulating equations is all about balance.
Steps to Solving a Single Variable Problem
Let us take a typical variable expression and break it into the steps needed to solve it.
$14−2x+2+6x=64.$ Find ${1/2}x.$
#1: Combine like terms
If there is more than one term with a same variable, we must combine them in order to ultimately isolate that variable. We can add or subtract terms with a same variable in the same way we can any other numbers.
$14−2x+2+6x=64$
Here we have a $−2x$ and a $6x$ (notice how we had to keep the signs in front of the numbers intact). Now we add them together.
$−2x+6x=4x$
We also have multiple numbers without variables on the left side of our equation. We must combine these as well, as they are also like terms.
$14+2=16$
So now, when we put the pieces together, our equation looks like this:
$16+4x=64$
#2: Isolate the term with your variable
Once we have combined our variables, we must isolate the variable term. If the term is simply the variable itself (e.g. $x$), then we can skip this step. But since our term here is $6x$, we must isolate the whole term first.
$16+4x=64$
We have a positive 16 here that we want to get rid of in order to isolate our $4x$. This means we must subtract 16 from both sides of our equation. Why? Because we have a positive 16, which means that it is addition. And subtraction is the opposite of addition.
We must also subtract 16 from either side to cancel out the 16 on the first expression (make it zero) so that we can isolate our variable.
$16−16+4x=64−16$
$4x=48$
#3: Isolate your variable
Now that we’ve isolated our term ($4x$), we can further isolate the variable.
Again, we perform an opposite function of the term. In this case, we have $4x$, which uses multiplication. In order to isolate the variable, we must therefore use division (the opposite of multiplication) by dividing by 4 on both sides. This will set our x equal to one and thus isolate it.
$4x=48$
${4x}/4={48}/4$
$x=12$
#4: Double-check your variable by plugging it back in
Now that we’ve solved for our variable, let us check to make sure it is correct by plugging it back into the original equation.
$x=12$
$14−2x+2+6x=64$
$14−2(12)+2+6(12)=64$
$14−24+2+72=64$
$−10+74=64$
$64=64$
Success! We have correctly isolated the variable and found its value.
#5: And, finally, double-check to make sure you are answering the right question.
Ah-ha! We can’t stop here. Our initial question asked for the value of $1/2x$, not just x by itself. If we had stopped here at $x=12$, we would have gotten the final answer wrong.
Now, we end the problem by saying:
${1/2}x=(1/2)12=6$
So our final answer is 6.
Always be sure to double-check both that your variable is correct and that you are answering the exact question the test is asking you to answer.
Now let’s try it again with our given equation problem from earlier.
We have ${1/3}y+9=0$ and we must isolate our variable in order to ultimately find the value of y
Step 1, combine like terms:
There are no like terms to combine, so we can skip step 1.
Step 2, isolate the variable term:
$1/3y+9=0$
$1/3y+9−9=0−9$
$1/3y=−9$
Step 3, isolate the variable:
$1/3y=−9$
$3*1/3y=−9$
$y=−27$
Step 4, double-check answer:
$1/3y+9=0$
$(1/3*−27)+9=0$
$−9+9=0$
$0=0$
Step 5, double-check if answering the right question:
The initial question wanted us to find y, and that is exactly what we found. We can confidently say that we are finished.
Success! Our final answer is A, -27.
Ready to put your single variable equation knowledge to the test?
Test Your Knowledge
1.
2.
3.
4.
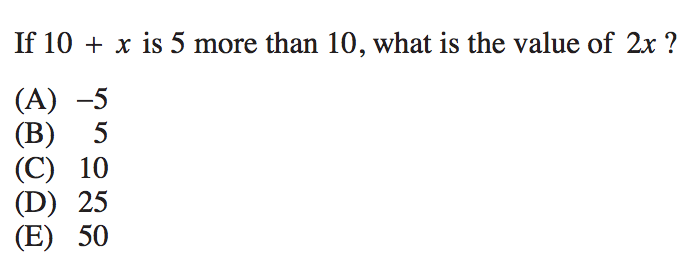
Answers: 700, B, A, C
Answer Explanations:
1. This problem is one to be cautious of because you'll note that your final answer is NOT your variable. Why? Because we are asked to find the total amount of money each person made during the week and yet our variable is the amount of sales they made.
So let's walk through the problem and set up our equation.
We are told that both Tom and Alison made the same amount of money in a certain week, which means that this is an equation problem (their earnings are set equal to one another).
We also know they had the exact same number of sales and that this number is yet unknown. This is our single variable. Let us call it x.
Tom made 300 dollars plus 20% of his sales. We can set up his half of the equation like so:
$300+0.2x$
(For more on percentages and why we can set up 20% of x as $0.2x$, check out our guide to SAT fractions and ratios.)
Alison made 200 dollars plus 25% of her sales. So we can set up her half of the equation thusly:
$200+0.25x$
Now, let us set the two sides equal to one another and solve for our variable.
$300+0.2x=200+0.25x$
First, let us combine our like terms by moving them to opposite sides of the equation:
$300−200=0.25x−0.2x$
$100=0.05x$
Now, let's isolate our variable:
$100/0.05={0.05x}/0.05$
$2000=x$
This means that they each sold 2000 dollars worth of product.
But wait! We can't stop here. The question asked us to find their weekly compensation, NOT their weekly sales. We must plug 2000 back into one of the original equations in place of x to find our final answer.
Let's take Tom's weekly earnings again:
$300+0.2x$
$300+0.2(2000)$
$300+400$
700
So both Tom and Alison (remember, they made the same amount) earned 700 dollars that week.
Our final answer is 700.
(Note: you can also double-check your answer with Alison's original equation as well:
$200+0.25x$
$200+0.25(2000)$
$200+500$
700
Either way, the answer is 700)
2. We are told that a triangle has a perimeter of 13 and one side length of 3. The other two sides are equal. That means we would set up an equation that would look like this:
$3+2x=13$
The left side of the equation is the sum of all the triangle’s sides. x is substituting for our unknown side lengths. And we have multiplied our x by 2 because the two unknown side lengths are equal. Now, we solve.
$3+2x=13$
Subtract 3 from both sides
$3−3+2x=13−3$
$2x=10$
Isolate our variable
${2x}/2=10/2$
$x=5$
So each of the other side lengths must be equal to 5. Let’s plug the answer back in to make sure this is correct.
$3+5+5=13$
$13=13$
Success! And we are being asked for the length of each side, so we know that our variable answer is the final solution.
Our final answer is B, 5.
3. We are being asked to find the number of sandwiches that Ali made, so let’s make our unknown variable a for Ali.
This means that Ali made a number of sandwiches. We are told that Ben made three times as many sandwiches as Ali, which means that Ben made $3a$ sandwiches.
Now Carla made twice as many sandwiches as Ben. We will still say that all the sandwiches made are in terms of a number of sandwiches, so Carla made $2*3a=6a$ sandwiches.
And we also know that the total number of sandwiches was 20. So now, when we put it all together, we get:
$a+3a+6a=20$
Combine our like terms and we get:
$10a=20$
Isolate our variable.
${10a}/10={20}/10$
$a=2$
Now let’s double-check to make sure that is correct.
If Ali makes 2 sandwiches, and Ben makes three times as many, he will have made 6 sandwiches. If Carla makes twice as many as Ben, she’ll have made 12 sandwiches.
$2+6+12=20$
20=20
Success! We have correctly isolated our variable.
Since we said that a was the number of sandwiches that Ali made, this means:
Our final answer is A, Ali made 2 sandwiches.
4. We are given the problem: "$10+x$ is 5 more than 10." The "is" in the question sets the terms equal, so when we translate this statement, we get:
$10+x=15$
Now, let’s isolate our variable.
$10−10+x=15−10$
$x=5$
Now let’s double-check by plugging our x back into the original equation.
$10+x$ is 5 more than 10.
$10+5=15$ is 5 more than 10.
Success, we have isolated our variable. But wait! The final question wants us to find the value of 2x, not just x.
$x=5$
$2(5)=10$
So our final answer is C, $2x=10$
Whoo! You conquered those single variable equations!
The Take Aways
Single variations make up the backbone of many other SAT problems. By knowing how to manipulate these kinds of expressions, you’ll be able to build on these techniques to solve much more complex problems and equations.
Just remember to always perform the same act to each side of the equation and save isolating your variable for last, and you’ll be conquering single variable equations left and right.
Now you’ve got the building blocks for understanding how to go forth and take on the rest of the SAT math topics. So build upon this knowledge and tackle the rest of what SAT math has to offer.
What’s Next?
You’ve build up your mathematical foundation and now you’re raring to take on more. Before you start in on another SAT math topic guide, make sure you have a good idea of all the topics covered on the SAT math.
Think you might need a tutor? Check out the best ways to find a tutor that suits your needs, whether online or in person.
Taken a practice test and don’t know how you match up for schools? Make sure you have a good idea of what your ideal score truly is.
And if you feel like you’ve got a handle on the math itself, but struggle with the timing, then be sure to check out our guide on how to complete your SAT math section on time.
