
One of the ACT’s absolute favorite shapes is the circle (or at least we assume so, given how often circles show up on the test). You will not be given any formulas on the ACT, so you’ll have to know and memorize the ins and outs of how circles work before test day. And, considering how often circles show up, mastering circle problems is definitely in your best interest.
This will be your complete guide to ACT circles, including areas, circumferences, degrees, arcs, and points on a circle. We’ll take you through what these terms mean, how to manipulate and solve for various aspects of a circle, and how to tackle the most difficult ACT circle questions you may see on test day.
What Are Circles?

A circle is formed from the infinite number of points equidistant (the same distance) from a single point--the center of the circle. A circle is also a two dimensional shape, which means it is completely flat.
So any and all straight lines drawn from the center will exactly hit the edge of the circle as long as all the lines are of equal length.
Degrees and Radians
A circle is measured in either degrees or radians. Both are ways to express either the whole circle or pieces of the circle.

A full circle has 360 degrees. A semicircle (half a circle) has $360/2 = 180$ degrees, which is why a straight line equals 180 degrees.
To find a piece of a circle, you must find it in relation to 360 degrees. So an eighth of a circle is $360(1/8) = 45$ degrees, and a third of a circle is $360(1/3) = 120$, etc.

Just as a circle has 360 degrees, you could also say that it has $2π$ radians. You find the radian measure of pieces of a circle the exact same way that you found pieces of a circle using degrees.
So an eighth of a circle in radians is $2π(1/8) = π/4$ radians and a third of a circle in radians is $2π(1/3) = {2π}/3$ radians, etc. (For more information on radians, check out our guide to ACT trigonometry.)
Circumference

The circumference is the edge of the circle. It is made from the infinite points equidistant from the center.
Diameter

A diameter is any straight line drawn through the center of the circle which connects two opposite points on the circle’s circumference.
Radius

The radius of a circle is a straight line drawn from the center to any point on the circle’s circumference. It is always half the diameter.
Tangency

Circles are often described as “tangent” with one another. This means that they touch at exactly one point on each circumference. They might be inside one another (as in this picture), or they may touch "externally" at a single point.
<p < p="">π (pi)
If you’ve taken a geometry class, then you are also probably familiar with π (pi). π is the mathematical symbol that represents the ratio of any circle’s circumference to its diameter. It is usually expressed as 3.14(159), but its digits go on infinitely. (For more information on ratios, check out our guide to ACT ratios.)
Let's say we have a circle with a particular diameter (any diameter will do).

Now let's line up this same circle so that we have a series of the same diameter measurement all in a row.

Now, if we pick a point on the circumference of the circle and line it up at the beginning of the line, we can then "unroll" the circumference to see how long it is.

Once we unroll the circumference and lay it out flat, we can see that it measures a little over 3 times the diamter of the circle (specifically, 3.14159, or π, times the diameter).

No matter what the diameter of the circle, the circumference will always be π times that diameter. So, if a circle’s diameter is 1, then its circumference is π. And if its diameter is 2, then its circumference is 2π, etc.

You know all your definitions (whoo!), so now what? Well it's time to put the pieces together into our trusty circle formulas!
Circle Formulas
You will not be given any formulas on the test, so you will need to know these ACT circle formulas by heart in order to solve your circle problems. Let's look at all the formulas you'll need.
Circumference
$$c = πd$$
Because π is the relationship between a circle’s diameter and its circumference, you can always find a circle’s circumference as long as you know its diameter (or its radius) with the formulas:
$c = πd$ or $c = π2r$

Because the contestant must run around the course, she is running the circumference of the circle. And we are told that she will do so 3 times in order to complete her race.
So a 1-track loop would be:
$c_{1 \loop} = π2r$ (We are told that the radius is “$R$” so we can leave it as is.)
And a 3-track loop would be:
$c_{3 \loop} = (π2r) * 3$
$π6r$
So our final answer is K, $6πr$
Area
$$a = πr^2$$
You can also use π to find the area of a circle as well, since a circle’s area is closely related to its circumference. (Why? Because a circle is made of infinite points, and so it is essentially made up of infinite triangular wedges--basically a pie with an infinite number of slices. The height of each of these wedges would be the circle’s radius and the cumulative bases would be the circle’s circumference.)
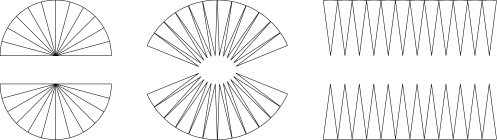
So you would be able to find a circle’s area using the formula:
$a = πr^2$

The dog’s leash represents the radius of the circle, because the dog can run 9 feet in any straight line from the center of the stake in the ground. So we must find the area of the circle using 3.14 for $π$ and 9 for the radius.
$a = πr^2$
$a = (3.14)(9^2)$
$a = (3.14)(81)$
$a = 254.34$
So our final answer is D, 254.
Arcs
$$c_\arc = πd({\arc \degree}/360°)$$
$$a_{\arc \sector} = πr^2({\arc \degree}/360°)$$
In order to find the circumference of a circle’s arc (or the area of a wedge made from a particular arc), you must multiply your standard circle formulas by the fraction of the circle that the arc spans.
To determine the fraction of the circle that the arc spans, you must have the degree measure of the arc and find its measure out of the circle’s full 360 degrees. So if you want to find the circumference of an arc that is 90°, it would be $1/4$ the total area of the circle. Why? Because $360/90 = 4$ (in other words, $90/360 = 1/4$).


In order to find the circumference measure of an arc, we must have both the degree measure and the circle’s radius or diameter. Luckily, we have all of these.
The degree measure of the arc, we are told, is 45.
The top diagram tells us that the diameter of the circle is 24 feet.
So the circumference of our arc is:
$c \arc = πd({\arc \degree}/360°)$
$c \arc = π24(45/360)$
$c = 3π$
Because we can see that our answer does not use units of $π$, let us convert our answer to digits by replacing $π$ with 3.14.
$3π = 3(3.14)$
$9.42$
We have successfully found the measurement of our arc, but we are not quite done. The question is asking us to find the full length of the zipper, which spans the length of the arc as well as the radius of the circle. This means we must find our radius and add it to our arc measurement.
The radius of the circle is 12. Why 12? Because our diameter is 24 feet and a circle’s radius is always half the diameter. $24/2 = 12$
So when we add our arc measure and our radius together, we get:
$9.42 + 12 = 21.42$
And the closest answer to match our measurement of 21.42 is answer choice G, 22.
This means our final answer is G, 22.
 With a dash of formula knowledge (and, presumably, some eye of newt), you can solve any and all circle problems. Magic!
With a dash of formula knowledge (and, presumably, some eye of newt), you can solve any and all circle problems. Magic!
Typical Circle Questions on the ACT
Circle problems on the ACT will be one of two types--diagram problem or word problem. Let us look at each type.
Diagram Problem
A diagram problem will give you a diagram from which to work. You must use the visual you are provided and either find a missing piece or find equivalent measurements or differences.
Helpful hint: often (though not always), the trick to solving a circle problem is in finding and understanding the radius. All lines drawn from the center to the circumference are radii and are therefore equal, and this will often play a vital part to solving the whole problem.

We are hoping to find the one statement that is NOT true, so let’s go through them and see which ones are accurate and inaccurate.
Answer choice F says that angle TUM is 65°. Well, we know that angle TMU must be 50° because it is opposite angle RMS and opposite angles are equal. (For more on this, check out our guide to ACT lines and angles.)
We also know that lines TM and MU are equal. Why? Because they are both radii of the circle (lines from the center to the circumference of the circle) and so they must be equal. This means that the triangle TMU is an isosceles triangle, which means that angles MTU and TUM are equal.
There are 180° in a triangle, so if we subtract 50°, we get:
$180 - 50 = 130$
This means that each of the angles MTU and TUM add up to equal 130. And, because they are equal, we can find their measure by dividing 130° in half.
$130/2 = 65$
So F is correct, angle TUM is 65°.
Now let’s look at option G, which says that lines RS and TU are parallel. We know this to be true. Why? Because together, the triangles form two diameters of the circle. And so straight lines downwards from where those diameters touch the circumference of the circle will be parallel.
H says that arc TXU measures 50°. We already know this to be true, because angle RMS measures 50° and its opposite angle is TMU, which must also measure 50°. Because the arc TXU contains and is made from angle TMU, its measurement must also be 50°.
Answer choice J says that line RM = line TM, which we also know is true. Why? Because they are both radii of the circle and so they must be equal.
By process of elimination, this must mean that K is wrong (and thus our final choice), but let’s make sure.
K says that lines RS and SM are equal, but we already know this cannot be true. Why? Because RM and MS are both radii and so they must be equal and angle RMS is 50°, which means the triangle is not equilateral. Because it is not an equilateral triangle, lines RM and TM cannot be equal. (Note: if this question was at all confusing to you, check out our guide to ACT triangles)
So our final answer is K.
Word Problem
Word problem questions about circles will describe a scene or situation that revolves around circles in some way. As you saw earlier in the section on areas and circumferences, word problem questions will often be a little more straightforward than a diagram question, as the picture is not given to you.
When given a word problem question, it is a good idea to do your own quick sketch of the scene. This will help you keep all the details in order.

Because this is a word problem, let us make our own picture of the scene.
First, we know that we have a circular table. We are told that is is 3 feet in diameter (in other words, 36 inches), so let us draw it.

Now, the tablecloth will be rectangular and will hang down at least 5 inches from any point on the circular table.

Finally, we need 1 more inch of tablecloth on every side (to sew down as a finishing touch).

Now, we can simply count our inches from top to bottom (or side to side) in a straight line. This will tell us the minimum length required for the fabric.
If we go from top to bottom, we can see that we will need:
$1 + 5 + 36 + 5 + 1$
$48$ inches of fabric.
Our final answer is K, 48.

Real life (and delicious) applications of circumferences and areas.
How to Solve a Circle Problem
When confronted with a circle problem, remember to employ these ACT math strategies:
#1: Write down your formulas at the beginning of the math section
As soon as you open up your ACT math section, take 20 seconds and write down your formulas. This way, you’ll have them as a reference for the rest of your allotted time, and you won’t worry about forgetting them in the heat of the moment when you’ll need them later on.
#2: Draw your own diagrams
If you’re not given a diagram, draw one yourself! It doesn’t take long to make your own picture and doing so can save you a lot of grief and struggle as you go through your test. It can be all too easy to make an assumption or mix up your numbers when you try to perform math in your head, so don’t be afraid to take a moment to draw your own pictures.
And if you are given a diagram, draw on it too! Mark down congruent lines and angles, write in your radius measurement or your given angles. Mark any and all pieces of information you need or are given. The reason not everything is marked in your diagrams is so that the question won’t be too easy, so always write in your information yourself.
#3: Analyze what’s really being asked of you
All the formulas in the world won’t help you if you think you’re supposed to find the area, but you’re really being asked to find the circumference. Always remember that standardized tests are trying to get you to solve questions in ways in which you’re likely unfamiliar, so read carefully and pay close attention to the question you’re actually being asked.
#4: Use your formulas
Once you’ve verified what you’re supposed to find, most circle questions are fairly straightforward. Plug your givens into your formulas, isolate your missing information, and solve. Voila!

A tasty mathematical conspiracy?
Test Your Knowledge
Now let's put your circle knowledge to the test on these real ACT math problems.
1.


2.

3.

Answers: B, B, H
Answer Explanations:
1. In order to determine the degree measure of a section of a pie chart, we must determine the fraction (or percentage) of the sector we’re working with compared to the whole amount of the circle.
In this case, we want to know what fraction of people total voted for Gomez in order to find how much of the pie chart the Gomez votes should be allotted.
If 40 people out of 200 voted for Gomez, then the Gomez votes are:
$40/200$
$1/5$ of all the votes total.
Because Gomez votes are $1/5$ of the total votes, then they should take up $1/5$ of the pie chart.
A circle is 360 degrees. So:
$(360)(1/5) = 72$
The arc sector of the Gomez votes will be at a 72 degree angle in the pie chart.
So our final answer is B.
2. We are given a diameter of 8 and we need to find the perimeter of the entire figure of two semicircles and a square.
Together, the two semicircles make a full circle with a diameter of 8, and their circumference makes up part of the perimeter. This means we must find the circumference of the circle the two semicircles make when put together.
$c = πd$
$c = π(8)$
So the circumference of the circle the two semicircles make is $8π$.
(Because we are dealing with semicircles, you could also find half of each of their circumferences by saying: ${1/2}c = 8π$ => $4π$. Each of their circumferences would be $4π$, so together, they would make: $4π + 4π = 8π$. Either way, the total circumference of the perimeter would be $8π$.)
Now we must add that to the rest of the perimeter, which is formed by part of the square. Two sides of the square (both measuring 8) make part of the perimeter, so we have:
$p = 8 + 8 + 8π$
$p = 16 + 8π$
So our final answer is B.
3. Because we are working with circles, we know that lines PS and PT are radii. Why? P is the center of the circle and points T and S lie on the circumference, so we know that the lines connecting them are radii.
Because PS and PT are equal and angle PST is 30 degrees, that means that angle PTS is also 30 degrees. Why? Angles opposite equal lines are equal (for more on this, check out our guide to ACT triangles).
This means we can find angle TPS as the shape is a triangle (which has 180 degrees total).
$180 - 30 - 30 = 120$
So angle TPS = 120 degrees.
Now that we have found angle TPS, we can also find angle RPS. Together, the two angles make a straight line, which means that they must equal 180 degrees total. (Why? Because a circle is 360 degrees and a semicircle is 180 degrees. A straight line will therefore always measure 180 degrees.)
$180 - 120 = 60$
This means that angle RPS = 60 degrees. And since angle RPS forms our arc, our arc measure it 60 degrees.
So our final answer is H.

Puppies cannot lie; it is scientific fact. You solved your ACT math problems and are, indeed, awesome.
The Take-Aways
Circle problems are quite common, but most of them are slight variations on the same themes of area and circumference. On the ACT, the most useful part of any circle is generally the radius and, once you’ve gotten used to thinking that all radii are equal, then you will often be able to breeze past even the trickiest of ACT circle problems.
Remember your formulas and keep a clear head about what’s being asked of you and you will be able to take out a significant portion of the ACT geometry section with circles alone.
What’s Next?
Now that you know all there is to know about ACT circles, make sure you're up to speed on all the other math topics on the ACT. Whether you need to brush up on solid geometry, trigonometry, ratios, or integers, you'll find what you need in our ACT math guides.
Running out of time on ACT math? We'll show you the tips and tricks you need in order to beat the clock.
Looking for a math tutor? Check out our guides on how to find the perfect ACT tutor for your needs.
Angling to get a perfect score? Our guide to an 800 on the math (written by a perfect-scorer) will tell you exactly how to reach those score goals by test day.











