Knowing your lines and angles is crucial for mastering SAT and is one of the foundational steps of geometry. Before you can tackle some of the more complex multi-shape problems that often appear towards the end of the test, you'll need to know just how to solve for all your missing angle measures.
Almost without fail, there will be exactly two problems on any given SAT on lines and angles (note: these problems are distinct from questions on lines and slopes). Though this is a small percentage of the test in and of itself, line and angle knowledge provides the backbone for other geometry problems and so should be ranked high on your studying priorities.
This will be your complete guide to lines and angles on the SAT—what they are, how you'll see them on the test, and how to solve these types of questions to maximize your points on test day.
Properties of Lines and Angles
Before we get into how lines and angles function, let's take a second to define what these terms mean.
A line is a completely straight marker, meaning it has no curvature. It can either have termination points (and will be called a "line segment") or go on infinitely. Its degree measure is always $180°$.
Parallel lines are two or more lines that are a set distance apart (equidistant) and never meet. They travel in the same direction continuously.
Perpendicular lines meet each other at 90-degree angles.
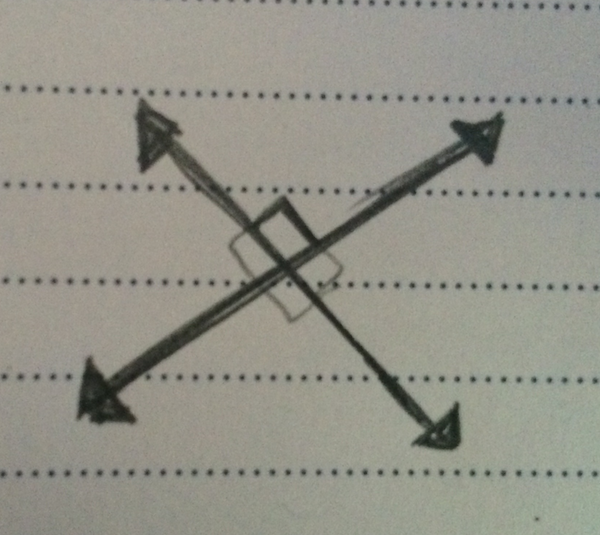
An angle is the meeting of two lines. The measure of how they meet is expressed in degrees, and the point at which they intersect is called the angle's "vertex."
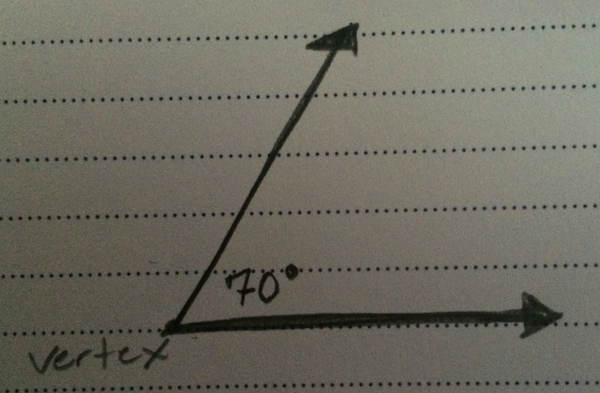
Line and Angle Equalities
Most of what you'll need to know about lines and angles on the SAT is when and how they will be equal or supplementary to one another.
Equal angles (or lines) are angles (or lines) that have the same measurement.
Supplementary angles are angles that add up to 180 degrees.
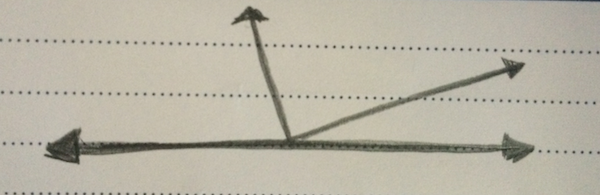
Because all these angles form a straight line and a straight line equals 180 degrees, the three angles are supplementary.
Opposite Angles
When two (or more) lines intersect, they form a series of opposite angles. Angles that are exactly opposite will always be equal to one another.
Now let's look at an opposite angle SAT problem.
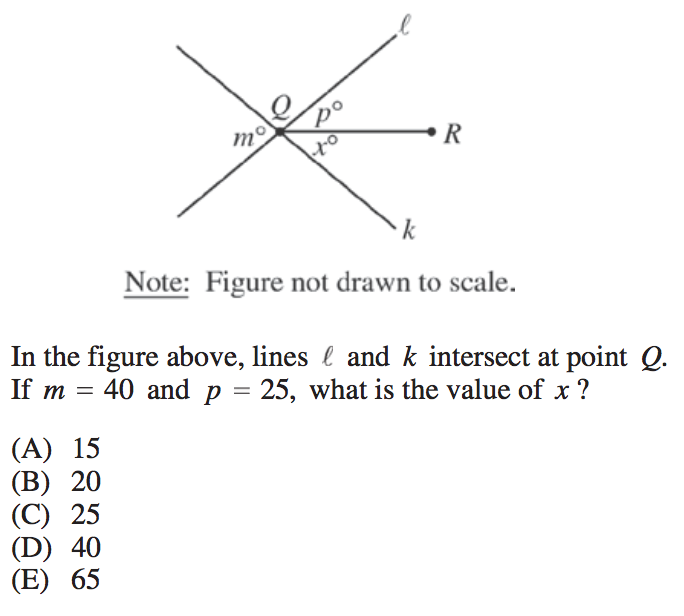
Here, you can see that the lines $l$ and $k$ intersect such that the sum of angles $p$ and $x$ make an angle that is exactly opposite angle $m$.
This means that, when we add together angles $p$ and $x$, their sum will be equal to angle $m$ (because opposite angles are equal).
$25+x=40$
$x=15$
So our final answer is A, 15.
Opposite Interior Angles
When there are two parallel lines that are crossed by another line (called a transversal), the angles on alternate interiors will be equal to one another. And the angles on the same side of the transversal line and the same side of their respective parallel lines will also be equal.
That may be difficult to picture, so let's look at a diagram:
(Note: when you are told that two lines are parallel on the SAT math section, the problem will almost always involve opposite interior angles in some way.)
Now let's look at an opposite interior angle SAT problem.
We are told that lines l and m are parallel, so that means the three vertical lines are transversals. We can see that the angle to the far left is marked as 89 degrees and it is an opposite interior angle to angle $r$ only.
This means that $r=89$ degrees, as opposite interior angles are equal.
So our final answer is A, $r$.
Typical Line and Angle Problems
Almost every line and angle problem is given to you as a diagram problem. You will be presented with a series of givens and then told to find a missing value of some kind. Almost always, this requires multiple steps and the use of multiple pieces of line/angle knowledge. For instance:
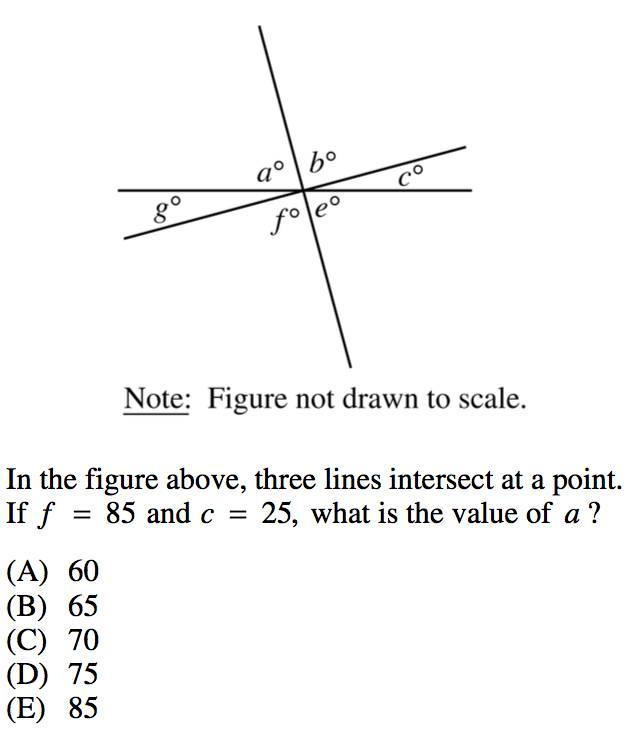
This is a very typical line and angle problem, so let's go through it.
We are told that angle $f$ is 85 degrees. This means we know that angle $b$ is also 85 degrees because it is opposite $f$ and opposite angles are equal.
We are also told that $c$ is 25 degrees. This means that $g$ must also be 25 degrees because it is opposite angle $c$.
And finally, we know that a line equals 180 degrees. This means that, in order to find angle $a$, we can say:
$a+25+85=180$
$a+110=180$
$a=70$
So our final answer is C.
As we said before, this question is representative of most line and angle problems you'll see on the test. Based on your givens, you must use your knowledge of opposite angles (opposite angles are equal) and your knowledge of the degree measure of a line (a line is 180 degrees) in order to put together all the clues and solve your problem.
The other kind of line and angle problem you may see will involve triangles. In these questions, you must not only put together multiple pieces of angle knowledge, but triangle knowledge as well.
Generally, you will not need to know more than the fact that all the interior angles in a triangle add up to 180 degrees, but check out our guide to SAT triangles if you are rusty on your triangle geometry.
Because we are told that lines l and m are parallel, we can guess that our answer likely has something to do with opposite interior angles. We also know that, to equal 180 degrees, our angles must either complete a triangle or a straight line.
With those clues in mind, let's go through our answer choices.
Option A gives us $k$, $n$, and $r$. We know from our opposite interior angles that $k$ and $r$ are equal, and that $n$, $s$, and $t$ are equal, but this information helps us complete neither a triangle nor a straight line. We can eliminate answer choice A.
Answer choice B gives us $k$, $p$, and $s$. Again, from our opposite interior angle knowledge, we know that $k$ and $r$ are equal, and that $n$, $s$, and $t$ are all equal.
Because $s=n$, we can form a triangle with our given angles. And because $s=t$, $p$ is given, and opposite interior angle equalities means that $k$ is equal to the unknown angle counterclockwise above $t$, then our known values can also form a straight line of 180 degrees.
Whether they are forming a triangle or a straight line, we can find 180 with the given angles of $k$, $p$, and $s$. We can stop here; we found our solution.
Our final answer is B.
You can see here that the linchpin for solving the problem was in your understanding that opposite interior angles are equal. And though you could have also found your required 180 degree measurement using a straight line (as we did above), it was faster to use the triangle.
For both ease of problem solving and knowing how to solve the more complex geometry problems, your knowledge of lines and angles should definitely be supplemented with triangle study. So don't forget to brush up on your SAT triangles!
Let's take a look at the tips for unlocking SAT angle problems.
Tips for Solving a Line and/or Angle Problem
As you saw in the earlier examples, most line and angle problems require you to go through multiple steps before you find the right answer. And most of the time, you must solve the question piece by piece in order to unlock the final solution.
As you go through this process, keep in mind these three tips:
#1: Write in your givens
If you are given a diagram in which your givens are NOT written in, then write them in yourself! Sometimes, seeing the numbers on the page can make all the difference in the world between a difficult problem and an easy one.
You'll also be far less likely to mix up your numbers and variables if you keep your work on the page instead of in your head.
#2: Work from your givens to find the next puzzle piece
Sometimes, it can be tricky to know where or when or in what order to work through a problem. Take a moment to find what you can before you worry about how to go forward.
If you have opposite angles, write in the measure of the angle opposite you're given. If you have angles that make a straight line, find the value of the missing variable. Immediately find the missing pieces that you can, and that information will often lead you straight to your solution.
#3: If necessary, use plugging in answers or plugging in numbers
If you find yourself stuck (or there is literally no other way to solve the problem), then whip out your PIA or PIN knowledge. Sometimes the process can be slower than a straight solve, but these strategies will almost always get you where you need to go and so can be worth the extra seconds.
Ready, set...go! Let's test that newfound knowledge!
Test Your Knowledge
1.
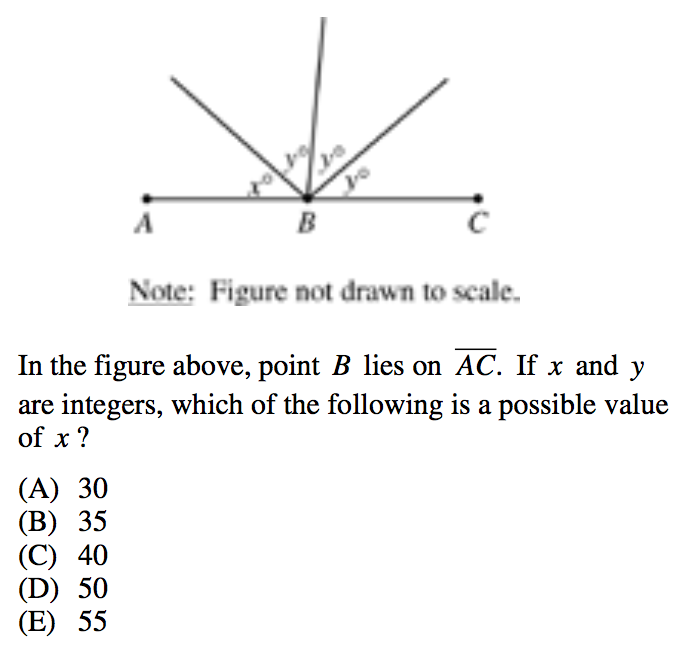
2.
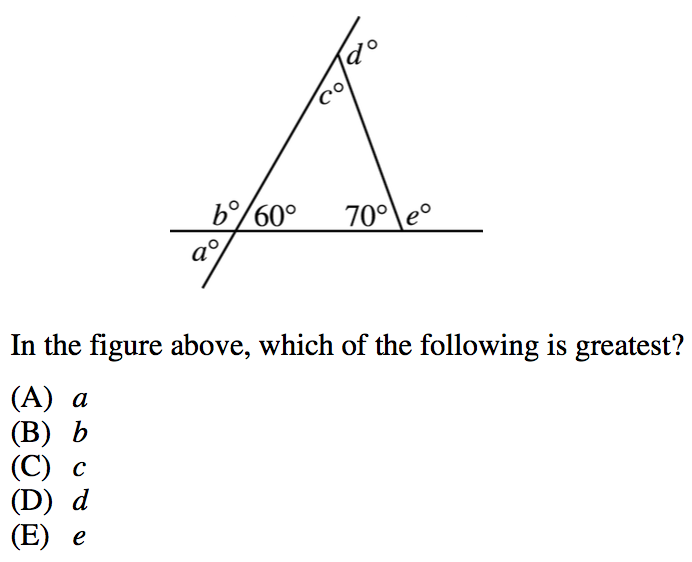
3.
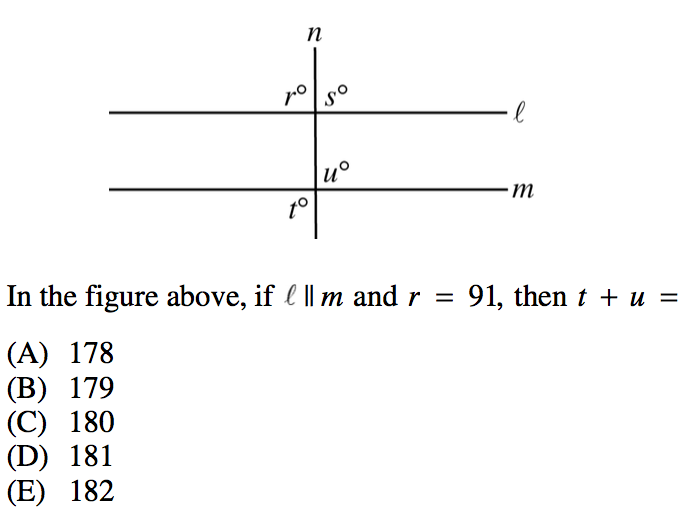
4.
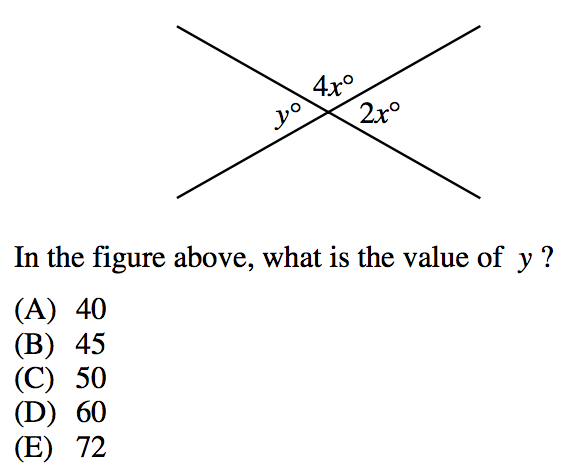
Answers: A, D, A, D
Answer Explanations:
1. This is a question that cannot be solved without using plugging in answers. We can see that $x$, $y$, $y$, and $y$ all make up a straight line (which equals 180 degrees). So let us express that as an equation.
$x+3y=180$
Now, we have no other information (other that that $x$ and $y$ are both integers), from the problem, so now we must look to the answers.
Let us start with the answers that end in 0 as those are easiest to work with. If these do not work, then we can eliminate them and try the answers that end in 5.
Let's begin by plugging in our middle value, C, in place of $x$.
If $x=40$, then:
$40+3y=180$
$3y=140$
$y=46.67$
140 is not evenly divisible by 3, so we can eliminate answer choice C.
Let us now try answer choice A, $x=30$.
$30+3y=180$
$3y=150$
$y=50$
When $x=30$, both $x$ and $y$ are integers. This fulfills our question premise and so is our correct answer choice.
Our final answer is A, $x=30$
2. Let us solve this question by finding the values of all the angles we can.
Angle $a$ is opposite the 60 degree angle, and so angle $a=60$.
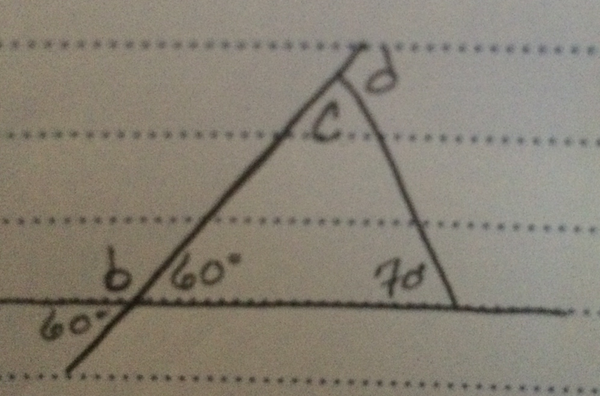
We can also see that angles $a$ and $b$ are supplementary, as they form a straight line. This means that:
$a+b=180$
$60+b=180$
$b=120$
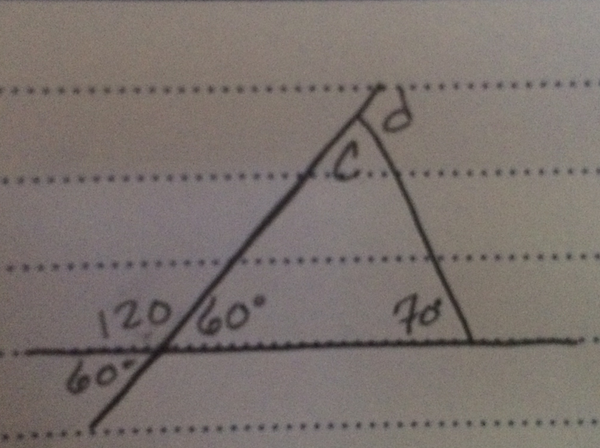
We can also see that angle e is supplementary with the 70 degree angle. So:
$e+70=180$
$e=110$
Now, we need only find angles $c$ and $d$. From our knowledge of triangles, we know that the interior degrees of a triangle add up to 180 degrees. So angle $c$ must be:
$c+60+70=180$
$c=50$
And because $c$ and $d$ form a straight line and are therefore supplementary, we can find angle $d$ by saying:
$c+d=180$
$50+d=180$
$d=130$
Which means, that of all the degree measurements that we found ($a=60$, $b=120$, $c=50$, $d=130$, and $e=110$), angle $d$ is the largest.
Our final answer is D, $d$.
3. Because we are told that lines $l$ and $m$ are parallel, we can guess that this problem likely involves opposite interior angles.
Because we are familiar with our opposite angles and our opposite interior angles, we can see that angles $s$, $u$, and $t$ are all equal.
We can also see that angles $r$ and $s$ are supplementary, as they form a straight line. And if $r=91$, then let us find angle $s$:
$r+s=180$
$91+s=180$
$s=89$
We already said that angles $s$, $u$, and $t$ are equal, so they are all equal to 89 degrees.
For the final step, we must add $t$ and $u$. So:
$t+u$ => $89+89=178$
So our final answer is A, 178.
4. In this question, we are working with multiple variables. Luckily, we can find our value for $x$ and then use it to find our $y$ value.
The angle measures $4x$ and $2x$ make a straight line, so they are supplementary. This means that:
$4x+2x=180$
$6x=180$
$x=30$
Now, we can find $y$ by using our $x$ value in one of two ways—either because angle $y$ is opposite (and therefore equal) to angle $2x$ or because angle $y$ makes a straight line with $4x$ (and is therefore supplementary).
So we can say that:
$y=2x$
$y=2(30)$
$y=60$
Or, we can say that:
$y+4x=180$
$y+4(30)=180$
$y+120=180$
$y=60$
Either way, our answer is $y=60$.
So our final answer is D.
Whoo! Your brain is on fire (in a purely metaphorical and non-lethal way, of course).
The Take-Aways
Lines and angles are often simpler than you may think. The tricky thing about these types of questions is generally in the number of steps it takes to get to the final answer.
Just remember your equalities, keep your work organized, and do your best to avoid careless errors. Once you've locked down lines and angles, you will be well equipped to take on the more and more complex geometry problems the SAT can put in front of you.
What's Next?
Raring to go and learn more about the many SAT math topics you'll see on the test? Well you're in luck! We've got guides upon guides on all the topics you'll need to know in order to rock the SAT math section, including probability, ratios, advanced integers, and more.
Don't know where to start? Make sure you have set a realistic goal for yourself and understand how your scores currently stack up.
Think you need a tutor? Check out how to find the right tutor for your needs, whether online or in person.
