Triangle questions account for less than 10% of all SAT math questions. That being said, you still want to get those questions right, so you should be prepared to know every kind of triangle: right triangles, isosceles triangles, isosceles right triangles—the SAT could test you on any one of them. Since triangle problems only account for a small percent of the SAT math questions, you shouldn’t spend all of your study time on triangles.
This article should be all you need to prepare you to tackle SAT triangle questions. I'll let you know the types of triangles that will show up on the SAT, their formulas, and the strategies you’ll need to apply when approaching a triangle question. I’ll also break down SAT math practice questions and explain how to knock triangle questions out of the park.
What Are Triangles?
First, let’s talk basics. A triangle is a flat figure made up of three straight lines that connect together at three angles. The sum of these angles is 180°.
Each of the three sides of a triangle is called a “leg” of the triangle, and the longest leg of a right triangle is called the “hypotenuse.” The angle opposite the hypotenuse will always be 90°, the largest of the three angles.
As we look at the many different types, you'll notice that many categories of triangles will be subsets of other categories of triangles and the definitions will continue to narrow.
Special Triangles
There are several different kinds of special triangles, all of which commonly appear on the SAT.
In this section, we will define and describe all the different kinds of triangles you’ll see on the test. In the next section, we will go through all the formulas you’ll need to know for your SAT triangle problems, as well as how to use them.
Equilateral Triangles
An equilateral triangle is a triangle that has three equal legs and three equal angles. Though the leg measurements can be anything (so long as they are all equal), the angle measurements must all equal 60°. Why? Because a triangle’s angles must always total 180°, and ${180}/{3}=60$.
Let's take a look at these types of triangles in action. NOTE: this question is a modified old SAT question in the style of the new SAT.
In the figure above, triangle ABC is inscribed in the circle with center O and diameter AC. If $\ov{AB}=\ov{AO}$, what is the degree measure of∠ABO?
(A) 15°
(B) 30°
(C) 45°
(D) 60°
Answer Explanation: We are told that two of the side lengths of the circle are equal, and we must find an unknown angle, ∠ABO. If you are familiar with your circles, then you know that any and all radii of a circle are equal.
Lines $\ov{AO}$ and $\ov{OB}$ are both radii of the circle, so they must be equal.
This means that all three legs of the circle BOA—lines $\ov {AO}$, $\ov {OB}$, and $\ov {BA}$—are equal. And we know that having three equal legs of a triangle means we have an equilateral triangle.
We also know that equilateral triangles have three equal inner angles, all of which are 60 degrees. This means that angle ABO is 60 degrees.
Our final answer is D, 60°.
Isosceles Triangles
An isosceles triangle is a triangle in which two sides and two angles are equal.
The sides opposite equal angles will always be equal, and the angles opposite equal sides will always be equal. This knowledge will often lead you to the correct answers for many SAT questions in which it seems you are given very little information.
Answer Explanation: Since the question tells you that $180−z=2y$ and $y=75$, we know that $180−z=(2)(75)$ and solving that gives you $z=30$. If $z=30$, then each of the base angles of the isosceles triangle on the right must measure 75°(${180−30}/{2}$). Therefore, the angle marked $x°$ is $180°−75°=105°$, and so the value of $x$ is 105. The answer is 105.
Right Triangles
A right triangle is a triangle in which one of the angles measures 90° (90° is a right angle). This means that the sum of the other two angles must be 90° as well since a triangle’s angles always add up to 180°.
Special Right Triangles
There are many different kinds of right triangles and some are considered “special.” These are triangles that have set angles or side lengths and formulas to correspond with them. Understanding these types of triangles (and their formulas) will save you a significant amount of time on triangle questions.
We'll go through the formulas that correspond to these types of triangles in the next section, but for now, let’s go through their definitions.
Isosceles Right Triangle
An isosceles right triangle is just what it sounds like—a right triangle in which two sides and two angles are equal.
Though the side measurements may change, an isosceles triangle will always have one 90° angle and two 45° angles. (Why? Because a right triangle has to have one 90° angle by definition and the other two angles must add up to 90°. So ${90}/{2}=45$.
30-60-90 Triangles
A 30-60-90 triangle is a special right triangle defined by its angles. It is a right triangle due to its 90° angle, and the other two angles must be 30° and 60°.
It's also half of an equilateral triangle. As I mentioned earlier, an equilateral triangle has three equal angles all measuring 60°. If you attached another 30-60-90 triangle to this one (along the leg opposite the 60°), you'd have an equilateral triangle with all angles measuring 60°.
3-4-5, and 5-12-13 Right Triangles
3-4-5 and 5-12-13 triangles are special right triangles defined by their side lengths. The numbers 3-4-5 and 5-12-13 describe the lengths of the triangle’s legs, meaning that, when you have a right triangle with one leg length 4 and with a hypotenuse length 5, then you automatically know that the third leg equals 3.
Any consistent multiples of these numbers will also work the same way. So a right triangle could have leg lengths of:
3(1)-4(1)-5(1) => 3-4-5
3(2)-4(2)-5(2) => 6-8-10
3(3)-4(3)-5(3) => 9-12-15
And so on.
These are considered “special” right triangles because all of their sides are integers.
Recognize this handsome fellow? Because Pythagoras is here to impart his triangle wisdom.
Triangle Formulas
Now that you know what all your triangles will look like, let’s go through how to find missing variables and information about them.
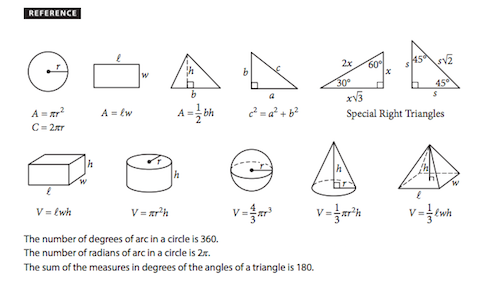
This is the box of formulas you will be given on every SAT math section. Though all the formulas you’ll need to know for triangles are all included, you must understand how and why these formulas work as well as when to use them. It will also save you time and effort to memorize these rather than flipping back and forth between the problem and the formula box.
So memorize your formulas if possible and read below to see what these formulas mean and how to use them. All the formula boxes in the world aren’t worth the paper they’re printed on if you don’t know how to apply them when solving your problems.
All Triangles
Some formulas apply to all triangles while other formulas only apply to special triangles. So let's first look at the triangle formulas that apply to any and all types of triangles.
Area
$$a= {1}/{2}bh$$
$b$ is the base of the triangle, which is the length of any one of the triangle’s legs.
$h$ is the height of a triangle, found by drawing a straight line (at a 90° angle) from the base of the triangle to the opposite angle from the base.
This means that, in a right triangle, the height is the length of the leg that meets at a 90° angle to the base. In a non-right triangle, you must create a new line for your height.
Perimeter
p=l1+l2+l3
Just like with any other kind of plane geometry figure, the perimeter of a triangle is the sum of its outer sides (the triangle’s three legs).
Right Triangles
There are also formulas that apply to right triangles and to specific types of right triangles. Let's take a look.
Pythagorean Theorem
a2+b2=c2
The Pythagorean theorem allows you to find the side lengths of a right triangle by using the lengths of its other sides. a and b signify the shorter legs of the triangle while c is always the leg opposite the 90° angle (the hypotenuse).
3-4-5 and 5-12-13 triangles (and their multiples) are special because you do not need to work through the Pythagorean Theorem in order to find the side measures of the third length (though, of course, you always can). Remember, if one side of a right triangle is 8 and its hypoteneuse is 10, then you automatically know the third side is 6.
Trigonometric Formulas: Sine and Cosine
Trigonometry makes up less than 5% of all math questions, but you won't be able to answer any trigonometry questions correctly without knowing trigonometry formulas. Check out our trigonometry guide to learn all the formulas you need to know and to learn how to apply the formulas to SAT math questions.
Isosceles Right Triangle
x, x, x√2
Though you can find the missing side lengths of an isosceles triangle using the Pythagorean theorem, you can also take a shortcut and say that the equal side lengths are each x, and the hypotenuse is $x√2$.
Why does this work? Well, think about an isosceles triangle with a leg length of 6.
We know the second leg must also equal 6 because the two legs are equal in an isosceles triangle. And we can also find the hypotenuse using the Pythagorean theorem because it is a right triangle. So:
62+62=c2
36+36=c2
72=c2
$$c = √72$$
$c = √36 * √2$ (Why were we able to split up our root this way? Check out our guide to SAT advanced integers and its section on roots if this process is unfamiliar to you.)
$c = 6√2$
So, we are left with side lengths of 6, 6, and $6√2$. Or, in other words, our side lengths are x,x, and $x√2$.
30-60-90 Triangle
$$x, x√3, 2x$$
Just like with an isosceles right triangle, a 30-60-90 triangle has side lengths that are dictated by a set of rules. Again, you can find these lengths with the Pythagorean theorem, but you can also always find them using the rule: $x, x√3, 2x$, where $x$ is the side opposite 30°, $x√3$ is the side opposite 60°, and $2x$ is the side opposite 90°.
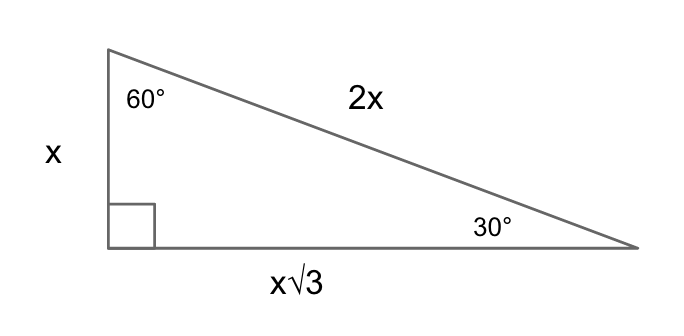
This knowledge can help you find the lengths of sides when given a more complex triangle problem.
Studious!Dog is proud of your studiousness right now. (So much studious.)
Typical Triangle Questions
Let’s look at some of the standard types of question in each category. NOTE: the question examples provided are not from official SAT tests since the newly redesigned SAT doesn't start until March 2016. These questions have been taken from College Board new SAT practice tests or adapted from other College Board study materials for the new SAT.
#1: Finding Missing Values
Most triangle problems will fall into this category—you will be asked to find a missing angle, an area, a perimeter, or a side length (among other things) based on given information.
Some of these questions will be more complicated than others, but the SAT will always provide you will enough information to solve a problem, so it’s up to you to put the clues together.
Let’s walk through an example question of this type:
Note: Figure not drawn to scale.
In the figure above, line m is parallel to line n, line d is perpendicular to line n, and line e intersects line m and line n. What is the length of x?
Answer Explanation: Since line d and line e intersect at C, >ACB and ∠DCE are vertical angles, and therefore they are equal in measure. Since line m is parallel to line n, ∠DEC and ∠CAB are alternate interior angles of parallel lines cut by a transversal, and so the measures of ∠DEC and ∠CAB are equal. By the angle-angle theorem, triangle ABC is similar to triangle EDC with vertices A, B, and C corresponding to vertices E, D, and C, respectively.
Also, triangle EDC is a right triangle, so you can use either the Pythagorean theorem or your knowledge of 3-4-5 right triangles to find that the hypotenuse is 5.
Since triangle ABC is similar to triangle EDC, the ratios of the lengths of corresponding sides of the two triangles are the same so ${CD}/{BC}={3}/{5}={DE}/{AB}={4}/{x}$.
Solving for $x$, we get $3x=20$. Therefore, $x={20}/{3}$.
#2: Ratios and (In)Equalities
These kinds of questions will generally ask you to either find the ratios between parts of different triangles or will ask you whether or not certain sides or angles of triangles are equal or unequal.
Answer Explanation: Angles ABE and DBC are vertical angles (meaning they are pairs of opposite angles made by two intersecting lines), and, therefore, they have the same measure. Since segment AE is parallel to segment CD, angles A and D are of the same measure by the alternate interior angle theorem. Since all angles are equal in triangles ABE and DBC, triangle ABE is similar to triangle DBC, with vertices A, B, and E matching up to vertices D, B, and C, respectively. Therefore,
Solving this you get CB = 4, and so CE = CB + BE = 4 + 8 =12.
#3: Multi-Shape or Shapes Within Shapes
As you can see from earlier examples, some of the triangle problems on the SAT will involve multiple triangles (or other geometric shapes) combined together. This technique for presenting problems is designed to challenge your understanding of lines and angles as well as triangles.
For these types of problems, you must use the information you are given and solve for more information down the line until you find exactly what you need. It’s essentially a domino effect of problem-solving.
Answer Explanation: The question tells you that ∠AEB and ∠CDB have the same measure. Since ∠ABE and ∠CBD are vertical angles (meaning they are pairs of opposite angles made by two intersecting lines), they have the same measure. Triangle EAB is similar to triangle DCB because the triangles have two pairs of congruent corresponding angles (angle-angle criterion for similarity of triangles). Since the triangles are similar, the corresponding sides are in the same proportion:
$${CD}/{x}={BD}/{EB}$$
Substituting the given values of 800 for CD, 700 for BD, and 1400 for EB in ${CD}/{x}={BD}/{EB}$ gives ${800}/{x}={700}/{1400}$
Therefore, $x={(800)(1400)}/{700}=1600$.
The final answer is 1600.
#4: Variables and Combination Variables
Finally, triangle problems that involve multiple variables (or only variables) in both the problem and the answer are usually located somewhere in the last three questions of any SAT math section. This means they are some of the most challenging types of math problems for the majority of students.
The good news is that there are many different ways to solve these types of problems and that a little time, organization, and creativity will almost always get you to your correct answer.
Considering these kinds of problems involve multiple variables, it is probably a good idea to check out the strategy of plugging in numbers if you haven’t done so already. This is a great technique to use if you are hesitant about the geometry and/or the algebra, or simply if multiple integers bother you.
Let’s take a look at an example problem of this type and the various methods of solving it.
Which of the following expresses $z$ in terms of $x$ and $y$?
(A) $2x+3y−180$
(B) $x+2y−180$
(C) $180−x−y$
(D) $360−2x−3y$
As you can see, this is a triangle problem that uses multiple variables and so is a bit complicated. Let’s look at all our options for solving the question:
Solving Method 1: Plug in our own numbers
On most any occasion in which you are given several variables in the question or in the answer options, a sure-fire technique you can use is the one of plugging in your own numbers. (For more on this strategy, check out our guide to plugging in numbers.)
We are given the variables $x$ and $y$ and told to find $z$. So let us choose some values for $x$ and $y$ that seem appropriate and use them to find $z$.
Let us just say that $x=60$ and $y=70$. Why those numbers? Why not!
Because the angles of a triangle always add up to 180°, we can find the missing values in our two bottom triangles by saying:
$$180−60−70=50$$
This means we can also find the value of the missing angle in our top triangle because we know that a straight line must also equal 180°. So:
$$180−50−50=80$$
Which means we can finally find the value of z by saying that:
$$z=180−80−70$$
$$z=30$$
Now, let us use the same values for $x$ and $y$ that we used in our problem to find which answer choice (or choices) gets us $z=30$.
Answer choice A gives us:
$$2x+3y−180$$
Which, when we replace our variables, is:
$$2(60)+3(70)−180$$
$$120+210−180$$
$$150$$
We are looking for an answer to match $z=30$, so this is far too large. We can eliminate answer choice A.
Let us try answer choice B:
$$x+2y−180$$
$$60+2(70)−180$$
$$60+140−180$$
$$20$$
This answer still does not equal 30, so we can eliminate answer choice B.
Answer choice C says:
$$180−x−y$$
But we already know that this is 50 and not 30, as we used this equation to find the missing components of our triangles earlier (180−60−70). We can eliminate choice C.
By process of elimination, answer choice D must be correct. But let us double-check to be sure.
$$360−2x−3y$$
$$360−2(60)−3(70)$$
$$360−120−210$$
$$30$$
Success! We have found an answer choice (and only one answer choice) that matches what we found for $z$.
Our final answer is D.
Solving Method 2: Algebraic approach
Alternatively, we could have found our answer using pure algebra and the properties of triangles, instead of filling in our own numbers. To do so, we would essentially be repeating the process we used to find our missing variables from above, but keeping the variables intact.
Each of the three triangles we are focusing on would all add up to 180°. We have three different triangles and three missing angles, so their equations would look like:
$$180−x−y$$
$$180−x−y$$
$$180−y−z$$
We know that all of those equations will find us one of the three unmarked angles. We also know that those three angles add up to 180°. (Why? Because they lie on a straight line, and a straight line equals 180°.)
So when we add the equations together and set them equal to 180°, we get:
$$(180−x−y)+(180−x−y)+(180−y−z)=180$$
$$540−2x−3y−z=180$$
$$−2x−3y−z=−360$$
$$−z=−360+2x+3y$$
$$z=360−2x−3y$$
So again, our final answer is D.
(Note: there is a third—and even faster—way to solve this problem that involves quadrilaterals. Check out our guide to SAT polygons for more info!)
Though there are many different types of triangle problems on the SAT, they tend to stand out from the crowd.
How to Solve a Triangle Question
Triangle questions are as numerous (comprising nearly 10% of the entire SAT math section) as they are varied. Because of this, it is difficult to break down one exact path for problem-solving triangle questions.
That said, your greatest assets and strategies when solving triangle problems will be to:
#1: Use Your Formulas (and Take Your Short-Cuts)
Using your formulas is the absolute most crucial step for any triangle problem. And, considering that most of your formulas essentially act as short-cuts (why bother solving with the Pythagorean theorem when you know that the legs of a 30-60-90 triangle are $x, x√3, 2x$?), you will save yourself a great deal of time and energy when you can keep your formulas on hand and in order.
#2: When Working With Multi-Shapes, Break It into Small Steps
Remember that dealing with a multi-shape triangle problem is like working with dominoes. Each successive piece of information makes way for finding the next piece of information.
Don’t get intimidated by the idea that you don’t have enough information or that there are too many shapes or lines to deal with. You will always have enough data to go on—just focus on finding one shape and one piece of information at a time, and the dominoes will fall into place.
#3: Draw It Out
Draw your own diagrams if you are given none. Draw on top of your diagrams when you are given pictures. Write in your givens and all the measurements you find along the way to your missing variable (or variables), and mark congruent lines and angles.
The more you can clarify your diagrams, the less likely you’ll be to make careless errors in misplacing or confusing your numbers and equalities.
#4: Plug in Your Own Numbers Whenever Possible
Finally, give yourself a break from dealing with variables and complex algebra if you need to. It can be far too easy to make a mistake when dealing with variables alone, so if you have the time to spare, go for plugging in your own numbers!
You have more information and strategies at your disposal than you think. Just keep them on hand and organized in your head and you'll be set.
Test Your Knowledge
Now let's test your triangle knowledge on more, SAT math problems. NOTE: these questions are not official SAT math section questions (since the newly redesigned SAT debuts in March 2016). These questions were taken from College Board practice tests for the new SAT or adapted from other new SAT practice questions and old SAT questions.
1.
Note: Figure not drawn to scale.
In the figure above, a regular polygon with 8 sides has been divided into 8 congruent isosceles triangles by line segments drawn from the center of the polygon to its vertices. What is the value of $x$?
Answer Explanation: The sum of the measures of the angles around a point is 360°. Since the 8 triangles are congruent, the measures of each of the 8 angles are the same. Therefore, the measure of each is ${360°}/{8}=45°$. In any triangle, the measure of the interior angles is 180°. So in each triangle, the sum of the measures of the remaining two angles is $180°-45°=135°$. Since the triangles are isosceles, the measures of the two angles are the same. Therefore, the measure of each of these angles is ${135°}/{2}=67.5°$.
2.
Note: Figure not drawn to scale.
In triangle ABC above, $AB=AC$, E is the midpoint of $\ov{AB}$, and D is the midpoint of $\ov{AC}$. If $AE = x$, and $ED = 4$, what is the length of $\ov{BC}$?
(A) 6
(B) 8
(C) $2x$
(D) $4x$
Answer Explanation: As always, let us first fill in our given information.
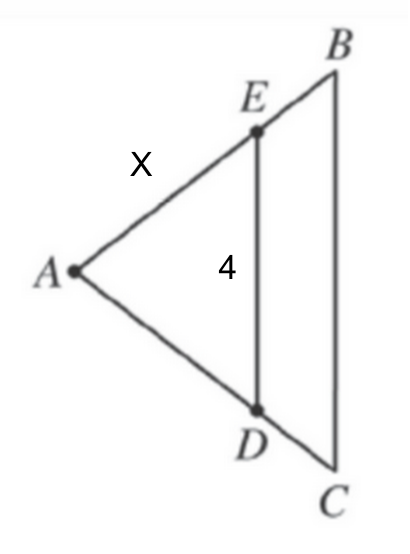
Now, though it may not look it, we are told that E is the midpoint of line AB. This means that, if segment AE is worth $x$, then segment EB is also worth $x$. This also means that the entire length AB will, therefore, be worth $x+x=2x$.
So let us set up a proportion.
Leg AE will be to its base, ED, as the leg AB will be to its base, BC. So:
$${AE}/{ED}:{AB}/{BC}$$
$${x}/{4}:{2x}/{BC}$$
$$8x=BCx$$
$$8=BC$$
Our final answer is B, BC = 8.
3.
Note: Figure not drawn to scale.
Two isosceles triangles are shown above. If $180−x=3y$ and $y=20$, what is the value of z?
Answer Explanation: Since the question tells you that $180−x=3y$ and $y=20$, then $180−x=3y=60$, and solving that gives you $x=120$. If $x=120$, then each of the base angles of the isosceles triangle on the right must measure 30° (${180−120}/{2}$). Therefore, the angle marked $z°$ is $180°−30°=150°$, and so the value of z is 150. The answer is 150.
We think you've earned a break, don't you?
The Take-Aways
Triangles will show up, without fail, at least a few times on every single SAT (usually in about 1 to 3 problems). The good news is that you will be given multiple formulas to aid you through these types of questions, but the drawback is that the test is timed, and so you should only waste time going to your formula box if you are all out of options.
Know your definitions, try to memorize your formulas, and do your best to keep a clear head as you go through your test. And, as always, practice, practice, practice! The more experience you get in solving the variety of triangle questions the SAT can think to put in front of you, the better off you’ll be in slaying those triangle problems.
What’s Next?
Now that you've done your paces on your triangles, it's time to make sure you are prepared for all the math topics you'll see on the SAT. All of our math guides will take you through strategies and practice problems for all the topics covered on the math section, from integers, to ratios, circles to polygons (and more!).
Feeling anxious about test day? Make sure you know exactly what to do and bring to ease your mind and settle your nerves before it's time to take your SAT.
Running out of time on the SAT math section? Look no further than our guide to help you beat the clock and maximize your SAT math score.
Angling to get a perfect score? Check out our guide to getting a perfect 800, written by a perfect-scorer.
