
I spent several years tutoring students in SAT Math, and many found the section frustrating. The first test-takers for the new SAT in March felt the same. Some struggled because they felt their strong suit was English and were irked by the content, mental math, and the pacing of SAT Math. Others found that although they considered themselves excellent math students, they struggled to finish and get the score they want.
No matter what group they fell into, students tended to make the same seven mistakes on the SAT Math section. In this guide, I'll tell you what those mistakes are, give you examples, and let you know to avoid making these mistakes in the future.
Mistake 1: You Didn't Write Out All of the Steps
Some students hate writing out their work for math problems. I know; I'm one of them. Trust me, while SAT Math problems may look simple since they only require you to know basic math topics (i.e. no advanced calculus), these problems are actually quite intricate, requiring you to go through many steps to get the correct answer.
If you don't write out all of these steps, you can accidentally end up with the wrong answer. This is especially important in the non-calculator section where you're not able to rely on a calculator to help you find the correct answer.
Together, we'll work through this no-calculator SAT Math question and write out all of the steps:

To determine what the price per pound of beef was when it was equal to the price per pound of chicken, you need to first find the value of $x$ (the number of weeks after July 1) when the two prices were equal. The prices were equal when $b=c$; that is, when $2.35+0.25x=1.75+0.40x$.
$$2.35+0.25x=1.75+0.40x$$
You can find the value of x by reducing.
$$2.35(−1.75)+0.25x=1.75(−1.75)+0.40x$$
$$0.6+0.25x=0.40x$$
$$0.6+0.25x(−0.25x)=0.40x(−0.25x)$$
$$0.60=0.15x$$
$$x={0.60}/{0.15}=4$$
Then, to determine b, the price per pound of beef, substitute 4 for $x$ in b=$2.35+0.25x$, which gives $b=2.35+0.25(4)=3.35$ dollars per pound. Therefore, D is the correct answer.
When I initially attempted this problem, I didn't write anything down, and I accidentally added 1.75 to 2.35 instead of subtracting 1.75 from 2.35. Therefore, I got the wrong value for $x$, 27.33. Thankfully, when I plugged that into $b=2.35+0.25x$, I found that my answer wasn't one of the answer choices, so I caught my mistake. However, I'm lucky because I would have answered incorrectly otherwise.
You don't want to miss questions because you didn't write out all of the steps. This is arguably the easiest mistake to fix. Write out all your steps, and you'll never accidentally get a question wrong because you skipped a step!
Mistake 2: You Forgot Formulas
The SAT gives you some formulas at the start of each Math section. However, the College Board doesn't provide you with all of the formulas you need to know to answer every question in the SAT Math section.
Luckily, here at PrepScholar, we've created a complete list of all the formulas you need to know for SAT Math. Create flashcards to help you memorize these formulas. However, memorizing alone is not enough. If you have the formulas memorized, but don't know how to use the formulas, they're useless to you. The best way to practice using formulas is to do as many SAT Math problems as you can.
Let's work through this SAT Math question that you couldn't answer without knowing formulas and how to apply them:

If you didn't have your trigonometry formulas memorized (SOHCAHTOA), you would have no idea how to answer this question. It's impossible to answer this question without at least knowing the formulas for the sine and cosine of an angle.
Memorizing formulas is not only necessary to answer certain questions correctly, but it can also be a time-saving shortcut. If you were a formula whiz and knew the complementary angle relationship for sine and cosine, which is $sin(x°)=cos(90°−x°)$, you'd know immediately that the answer is $cos(90°−x°)={4}/{5}$ or $0.8$.
However, if you didn't know that formula, but knew the sine and cosine formulas, you could still solve this problem by constructing a diagram using the given information. It's a right triangle (which it has to be to use sine/cosine), and the sine of angle x is ${4}/{5}$. If $sin(x)={opposite side}/{hypotenuse}$, then the opposite side is 4 long and the hypotenuse is 5 long:
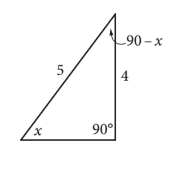
Since two of the angles of the triangle are of measure $x$ and 90, the third angle must have the measure $180°−90°−x°=90°−x°$. If we know that $cosine={adjacent side}/{hypotenuse}$, then, using the figure, $cos(90°−x°)={4}/{5}$ or $0.8$.
 SAT Math may make your brain hurt!
SAT Math may make your brain hurt!
Mistake 3: You Didn't Know Functions
Functions are one of the trickiest topics in SAT Math. This is not because they're more difficult than other topics, but rather students are simply less familiar with functions than they are with other math concepts. The good news is that you'll easily master functions with practice and familiarization.
Let's work through this SAT quadratic function question together:

To figure out which answer choice is the equation of the graph, you should start by finding the $y$-intercept. You can see in this graph that the $y$-intercept is 2, which means you can eliminate C and E since C had a $y$-intercept of -2, and E has no $y$-intercept.
The vertex of the graph is at $x=0$, so the function is not shifted to the right or left of the y-axis. This means that, in your quadratic equation $ax^2+bx+c$, your b value has to be 0. If it were anything other than 0, the graph would be shifted left or right of the y-axis.
Let's look at the remaining answer choices, A, B, and D, to see which one had a b=0. A does so that might be the correct answer, but let's rule out B and D. Answer choices B and D are squaring expressions, so let's FOIL them in order to see the equation properly.
Answer choice B gives us:
$$y=(x+2)^2$$
$$y=(x+2)(x+2)$$
$$y=x^2+2x+2x+4$$
$$y=x^2+4x+4$$
This equation has b=4, not b=0, so it can't be the answer. You can also eliminate D; when foiled, it gives us:
$$y=(x−2)^2$$
$$y=(x−2)(x−2)$$
$$y=x^2−4x+4, \so \b=-4$$
Therefore, A is the correct answer.
If you're still struggling, check out our full guide to functions. Remember, you'll master functions with practice, so take as many SAT math practice tests as you can.
Mistake 4: You Panicked at an Unfamiliar Question Format
SAT Math problems are often asked in strange ways that you've never seen in math class. When confronted with these unfamiliar question formats, many students rush to move on to the next question thinking they'll come back to it, or they'll just try to guess the answer. Even though you've reviewed all of the math content areas and knew your stuff, you don't think you know how to answer the question.
There is no easy solution to this issue. The only way to learn how to approach SAT Math questions is with practice. SAT Math questions are unlike the math questions you're used to seeing in your math class, so to get familiar with the SAT Math question style, you should take as many practice SAT tests as you can.
Let's work through this convoluted SAT Math problem together:

At first glance, this question looks overwhelming with a chart and a large paragraph. Don't let that scare you. Read carefully, and try to identify the important information as you read the question by circling or underling. Ask yourself: What am I solving for? What information am I given? How can I use this given information to find the solution?
We're trying to find the probability that a right-handed student selected at random is female. We're told that there are 5 times as many right-handed females as there are left-handed females, and there are 9 times as many right-handed males as there are left-handed males. Also, we know the total number of left-handed students is 18, and the total number of right-handed students is 122.
To solve this problem, you need to create a system of equations using two variables ($x$ and $y$) and the information you're given in the question. Let $x$ be the number of left-handed female students and let $y$ be the number of left-handed male students.
Using the information in the question, the number of right-handed female students will be $5x$ (since there are 5 times as many right-hand females as there are left-handed females) and the number of right-handed male students will be $9y$ (since there are 9 times as many right-hand males as there are left-handed males) .
Since the total number of left-handed students is 18 and the total number of right-handed students is 122, the system of equations below must be true:
$$x+y=18$$
$$5x+9y=122$$
When you solve this system of equations, you get $x=10$ and $y=8$. Thus, 50 of the 122 right-handed students are female. Therefore, the probability that a right-handed student selected at random is female is ${50}/{122}$, which to the nearest thousandth is $0.410$. The final answer is A.
 Don't run away from a weird question!
Don't run away from a weird question!
Mistake 5: You Solved for the Wrong Value
Because SAT Math questions can be convoluted, it's sometimes difficult to figure out what the question is asking you, which leads some students to solve for the wrong value. Take for example this SAT Math question:

This question throws a lot of numbers and letters at you. It gives you angle and side measures and mentions a similar triangle. Some students might accidentally solve for the measure of the sides of DEF. Don't let the numbers and letters distract you. Make sure to identify what you're being asked: what is the value of $sin F$?
To find $sin F$, we need to start with the given information: Triangle ABC is a right triangle with right angle B. Therefore, AC is the hypotenuse of right triangle ABC, and AB and BC are the legs of right triangle ABC. According to the Pythagorean theorem,
$$AB=√{(20^2)-(16^2)}=√{(400)-(256)}=√{144}=12$$
Since triangle DEF is similar to triangle ABC, with vertex F corresponding to vertex C, the measure of angle F equals the measure of angle C. Therefore, $sinF=sin C$, and $sinF={3}/{5}$. The final answer is ${3}/{5}$ or $.6$.
This problem has an easy fix: take the time to read the question fully, circle the important information, and make sure you know what you're being asked before you start doing any work.
I know you don't have a lot of time on the SAT Math section (that was one of the chief complaints from the new SAT test-takers), but you need to read each question completely and make sure that you know what you're being asked. You'll get better at this with practice.
Most SAT Math questions will have an answer choice that will seem correct if you misread the question. I know it's rude and sneaky; the SAT is trying to tempt you to answer incorrectly. Don't fall prey to the tricks! Read the question correctly, and you'll be on the track to get the right answer!
Mistake 6: You Used Your Calculator Incorrectly
Calculators are both wonderful and horrible. You only get to use your calculator on one part of the SAT Math section, but for that part, you need to use your calculator carefully. When you're rushing to answer SAT Math problems, you might accidentally type the wrong number(s) into your calculator, leading you to the wrong answer.
This is one of the better mistakes to make. Because if you type the wrong number(s) into your calculator, you'll likely find no matching answer in the SAT answer choices, and you'll realize you made an error. However, even if you catch the error, you've still wasted valuable time that you could have been using to answer more SAT Math questions.
Moral of the story: take the time to check that you've copied the numbers into your calculator correctly before running the calculation.
 Don't let your calculator become your enemy!
Don't let your calculator become your enemy!
Mistake 7: You Didn't Pace Yourself
With only 25 minutes to answer 20 questions in the no-calculator section and only 55 minutes to answer 30 questions in the calculator section, you need to learn to pace yourself. However, not every student should attempt the same pacing. You should plan your pacing based on your target SAT score.
In both math sections, the questions progress from easy to hard and then re-set on the grid-in portion from easy to hard. No matter what your target score is, you should always attempt the easier questions: the first half of the multiple choice and grid-ins.
If you're aiming for a Math section score above 700, then you're going to need to answer all or almost all of the 58 Math questions. That means you will need to get your pacing under one minute per question for the easier questions to conserve time for the harder questions.
If you're aiming for a Math section score below 700, then you can skip some questions. Focus your time on trying to answer the easier questions correctly (the beginning questions of the multiple-choice and grid-ins). Consider bubbling in a random letter for the harder questions since there is no penalty for guessing.
Note: if you use this strategy, make sure that you're answering enough questions to reach your target score. No one is perfect, so count on answering a few questions incorrectly. For example, if you're aiming for 600 in Math, then you should attempt at least 45 questions before bubbling in random answers for the other 13 questions. That way, if you answer five of the 45 incorrectly, you can still get 600. Give yourself a cushion.
To really master your pacing on the SAT Math section, you need to take a lot of practice tests under realistic testing conditions. For a more in-depth explanation on pacing, check out our guide to help you beat the clock and maximize your SAT math score.
What's Next?
Now that you know the most common mistakes on SAT math make sure you're prepared for all of the math topics you'll see on the SAT. All of our math guides will take you through strategies and practice problems for all the topics covered on the math section, from trig to radians, coordinate geometry to systems of equations and much more.
Feeling anxious about test day? Make sure you know exactly what to do and bring to ease your mind and settle your nerves before it's time to take your SAT.
Angling to get a perfect score? Check out our guide to getting a perfect 800, written by a perfect-scorer.












