
On the newly redesigned 2016 SAT, the math section content is divided into four categories by the College Board: Heart of Algebra, Problem Solving and Data Analysis, Passport to Advanced Math, and Additional Topics in Math. Heart of Algebra accounts for the largest part of the SAT math section (33% of the test), so you need to be well prepared for it. In this post, I'll be discussing this category's content and question types, working through practice problems, and giving tips on how to ace these questions.
Heart of Algebra: Overview
Content Covered
Just as the name would suggest, Heart of Algebra covers algebra content, but what algebra content specifically? These questions cover:
- Linear Equations
- System of Equations
- Absolute Value
- Graphing Linear Equations
- Linear Inequalities and Systems of Inequalities
I'll delve into each one of these content areas below. I'll explain exactly what you need to know in each area, and I'll walk you through some practice problems.
NOTE: All of the practice problems in this article come from a real College Board SAT practice test (Practice Test #1).
I'd recommend you don't read this article until after you've taken Practice Test #1 (so I don't spoil it for you!). If you haven't taken Practice Test #1, bookmark this article and come back after you've completed it. If you've already taken Practice Test #1, then read on!
Heart of Algebra Question Breakdown
As I mentioned at the start of the article, Heart of Algebra makes up 33% of the math section, which works out to 19 questions. There will be eight in section 3 (the non-calculator math test) and 11 in section 4 (the calculator math test).
Heart of Algebra questions vary in presentation. Because there are so many, the College Board needed to mix up how they ask you these questions. You'll see multiple-choice and grid-in Heart of Algebra questions. You may simply be presented with an equation(s) and need to solve or you might be given a real world scenario as a word problem and need to create an equation(s) to find the answer.
The SAT math section presents questions in order of difficulty (defined by how long it takes an average student to solve a problem and the percentage of students who answer the question correctly). You will see Heart of Algebra questions throughout the section: the straightforward, "easy" ones will appear at the beginning of the multiple choice and grid-ins while the more challenging ones that require you to create an equation or equations to solve will appear towards the end.
I'll give examples of each type of question (easy and hard) as we learn about each content area in the next section.
 We're on the path to conquering algebra!
We're on the path to conquering algebra!
Content Area Breakdowns
Linear Equations
Linear equation questions can be presented in a couple of ways. The easier linear equation questions will ask you to solve a linear equation that is given to you. The harder linear equation questions will ask you to write a linear equation to represent the given situation.
No Calculator Practice Problems
This question is one of the simplest, easiest and most direct Heart of Algebra questions that you'll see. The question just asks you to solve a linear equation without situating it in a real world situation that would require you to make sense of the context as well as the equation.

Answer Explanation:
Since $k=3$, one can substitute 3 for k in the equation, which gives ${x-1}/{3}=3$. Multiplying both sides of ${x-1}/{3}=3$ by 3 gives $x-1=9$, and if you add 1 to each side, then the result is $x=10$. D is the correct answer.
Tip:
If you struggled with this question, you could also solve it by plugging in the answer choices for x and seeing which one worked. Plugging in will work but will take you more time than simply solving the equation.
If you solve the equation to find x, you can double check your answer by then plugging it in. If you plug in your answer choice for x, and both sides of the equation are equal, you know you have the right answer!
The following question is slightly more challenging since it asks you to create a linear equation to represent the real world scenario it presents.

Answer Explanation:
There are two ways to approach this problem.
Approach 1: The total number of messages sent by Armand is equal to his rate of texting (m texts/hour) multiplied by the 5 hours he spent texting: m texts/hour × 5 hours = $5m$ texts. Similarly, the total number of messages sent by Tyrone is equal to his rate of texting (p texts/hour) multiplied by the 4 hours he spent texting: p texts/hour × 4 hours = $4p$ texts. The total number of messages sent by Armand and Tyrone is equal to the sum of the total number of messages sent by Armand and the total number of messages sent by Tyrone: $5m+4p$. C is the correct answer.
Approach 2: Pick numbers and plug them in. For example, I'm going to pick numbers and say Armand sends 3 texts per hour and Tyrone sends 10 texts per hour. Based on the given information, if Armand texts for 5 hours, Armand sent (3 texts per hour)(5 hours) texts or 15 texts; if Tyrone texts for 4 hours, Tyrone sent (10 texts per hour)(4 hours) texts or 40 texts. Therefore, the total number of texts sent by Armand and Tyrone is $15+40=55$ texts. Now, I plug in the numbers I chose to the answer choices and see if the number of texts matches 55 texts, so for answer C, $5(3) +4(10)=15+40=55$ texts. Therefore, C is the correct answer. NOTE: for this question, this strategy was slower, but for more complicated questions, this can be a faster and easier approach.
Tip:
Take these problems one step at a time. Figure out Armand's total number of text messages, then figure out Tyrone's total number of text messages, and then, combine them into one expression. Don't rush to jump to the final answer. You might make a mistake along the way.
Systems of Equations
System of equations questions will be presented in similar ways as linear equation questions; however, they're more difficult because you now have to do more steps and/or create a second equation.
The easier system of equation questions will ask you to solve for one variable when you're given two equations with two variables.
The harder system of equation questions will require you to write a system of equations to represent the given situation and then solve for one variable using the equations you created.
No Calculator Practice Problems
This question is arguably the simplest, easiest and most straightforward systems of equation questions that you'll see. It sets up the equations for you, and simply asks you to solve for x.

Answer Explanation:
Subtracting the left and right sides of $x+y=−9$ from the corresponding sides of $x+2y =−25$ gives $(x+2y)−(x+y)=−25−(−9)$, which is equivalent to $y=−16$. Substituting $−16$ for $y$ in $x+y=−9$ gives $x+(−16)=−9$, which is equivalent to $x=−9−(−16) =7$. The correct answer is 7.
Tip:
Plugging in may be a good option if you're given this question in the multiple-choice (which isn't the case here). However, you could have also plugged in your answer to double check your work!
Here is another fairly straightforward system of equation question, but it is slightly more difficult since you need to provide the answer for both x and y (which creates more potential for error).
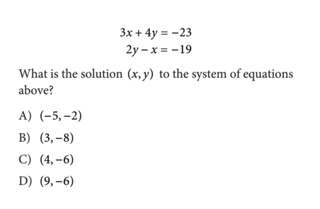
Answer Explanation:
Adding x and 19 to both sides of $2y−x=−19$ gives $x=2y+19$. Then, substituting $2y+19$ for x in $3x+4y=−23$ gives $3(2y + 19)+4y=−23$. This last equation is equivalent to $10y+57=−23$. Solving $10y+57=−23$ gives $y=−8$. Finally, substituting −8 for y in $2y−x=−19$ gives $2(−8)−x=−19$, or $x=3$. Therefore, the solution $(x, y)$ to the given system of equations is $(3, −8)$.
Tip:
Plugging in would have also been a quick way to solve this one! When asked to solve for both variables in a system of equation question, always try plugging in!
The following is a bit more difficult. Even though you're given the equations, you still need to determine what the question is asking you (which variable you need to solve for) which is slightly more challenging since it asks you the question using a real world scenario. Also, you need to solve it using mental math (since it's in the no calculator section).

Answer Explanation:
To determine the price per pound of beef when it was equal to the price per pound of chicken, determine the value of x (the number of weeks after July 1) when the two prices were equal. The prices were equal when $b=c$; that is, when $2.35+0.25x=1.75+0.40x$. This last equation is equivalent to $0.60=0.15x$, and so $x={0.6}/{0.15}=4$. Then to determine $b$, the price per pound of beef, substitute 4 for $x$ in $b=2.35+0.25x$, which gives $b=2.35+0.25(4)=3.35$ dollars per pound. Therefore, D is the correct answer.
Tip:
Take your time working through each step. It's easy to make a small mistake and get the wrong answer.
Calculator Practice Problem
The following is one of the hardest Heart of Algebra questions. Based on the real world scenario that you're given in the question, you need to create two equations and then solve them.

Answer Explanation:
To determine the number of salads sold, write and solve a system of two equations. Let $x$ equal the number of salads sold and let $y$ equal the number of drinks sold. Since the number of salads plus the number of drinks sold equals 209, the equation $x+y=209$ must hold. Since each salad cost 6.50, each soda cost 2.00, and the total revenue was 836.50, the equation $6.50x+2.00y=836.50$ must also hold. The equation $x+y=209$ is equivalent to $2x+2y=418$, and subtracting each side of $2x+2y=418$ from the respective side of $6.50x+2.00y=836.50$ gives $4.5x=418.50$. Therefore, the number of salads sold x was $x={418.50}/{4.50}=93$. Therefore, B is the correct answer.
Tip:
Take these problems one step at a time. Write out the equation for the total number of salads and drinks sold, then figure out the equation for revenue, and then, solve. Don't rush it or you might make a mistake.
Absolute Value
There will typically only be one Absolute Value question in the SAT math section. The question is usually pretty easy and straightforward, but it requires you to know the rules of absolute value to answer it correctly.Anything that is an absolute value will be bracketed with absolute value signs which look like this: || For example, $|-4|$ or $|x-1|$
An absolute value is a representation of distance along a number line, forward or backward.

This means that whatever is in the absolute value sign will become positive since it represents distance along a number line and it is impossible to have a negative distance. For example, on the above number line, -2 is 2 away from 0. Anything inside of the absolute value becomes positive.
This also means that an absolute value equation will always have two solutions. For example, $|x-1|=2$ will have two solutions $x-1=2$ and $x-1=-2$. Then, you solve each separate equation to find the two solutions, $x=3,-1$.
When working on absolute value problems, remember that you need to create two separate solutions the positive and the negative as we did above.
Calculator Practice Problem

Answer Explanation:
If the value of $|n−1|+1$ is equal to 0, then $|n−1|+1=0$. Subtracting 1 from both sides of this equation gives $|n−1|=−1$. The expression $|n−1|$ on the left side of the equation is the absolute value of $n−1$, and, as I just mentioned, the absolute value can never be a negative number since it represents distance. Thus, $|n−1|=−1$ has no solution. Therefore, there are no values for n for which the value of $|n−1|+1$ is equal to 0. D is the correct answer.
Tip:
Remember the rules of absolute value (it's always positive!). If you remember the rules, you should get the question right!
Graphing Linear Equations
These questions test your ability to read a graph and interpret it into $y=mx+b$ form. A quick refresher, $y=mx+b$ is the slope-intercept equation of a line, where m represents the slope and b represents the y-intercept.
In these questions, you'll typically be presented with the graph of a line, and you'll need to determine what the slope and y-intercept are to write the equation of the line.
Calculator Practice Problem


Answer Explanation:
The relationship between h and C is represented by any equation of the given line. The C-intercept of the line is 5. Since the points $(0, 5)$ and $(1, 8)$ lie on the line, the slope of the line is ${8-5}/{1-0}={3}/{1}=3$. Therefore, the relationship between h and C can be represented by $C=3h+5$, the slope-intercept equation of the line. C is the correct answer.
Tip:
Have the slope-intercept form ($y=mx+b$) and the slope equation $m={y_2-y_1}/{x_2-x_1}$ memorized. Know what each variable in the equations means. If you know all of this, you should be able to ace any graphing linear equation problem that you're given.
Linear Inequalities and Systems of Linear Inequalities
These are arguably the most challenging Heart of Algebra questions because many students struggle when variables are combined with inequalities. If you need a quick but in-depth refresher on inequalities, check out our inequalities guide.
These questions typically appear towards the end of the multiple-choice and grid-ins in each section. These questions will be presented as straightforward already set up inequalities (you won't be asked to create inequalities nor will you be presented with a real world scenario using inequalities). Although they're presented in a straightforward way, these questions are challenging, and it's easy to make a mistake, so take your time!
Calculator Practice Problems

Answer Explanation:
Subtracting $3x$ and adding 3 to both sides of $3x−5≥4x−3$ gives $−2≥x$. Therefore, x is a solution to $3x−5≥4x−3$ if and only if x is less than or equal to −2 and x is NOT a solution to $3x−5≥4x−3$ if and only if x is greater than −2. Of the choices given, only −1 is greater than −2 and, therefore, cannot be a value of x. A is the correct answer.
You could also try to answer this by plugging in the answer choices and seeing which one didn't work. If you plug in A into the inequality, you'd get $3(-1)-5≥4(-1)−3$. Simplifying the inequality, you'd get -8≥-7, which is not true, so A is the correct answer.
Tip
Remember the rules of inequalities! Take your time working your way through each step so that you don't make any mistakes. Also, remember to try plugging in the answer choices to find the correct answer!
Let's take a look at another example.

Answer Explanation:
Since (0, 0) is a solution to the system of inequalities, substituting 0 for x and 0 for y in the given system must result in two true inequalities. After this substitution, y < −x + a becomes 0 < a, and y > x + b becomes 0 > b. Hence, a is positive, and b is negative. Therefore, a > b. Choice A is correct.
Tip:
Treat this system of inequalities with four variables the same as you'd treat a system of inequalities with two variables. Remember that if (0,0) is a solution that means that when x=0, y=0.
4 Key Strategies for Heart of Algebra
I've interspersed the strategies for attacking these questions throughout this article in the "tip" sections, but I'll summarize them here now.
Strategy #1: Memorize the Rules and Formula
You need to know the rules of inequalities, the rules of absolute value, and the formula for the intercept-slope version of a line ($y=mx+b$) to answer those types of algebra questions correctly. Without the rules and formula, these questions are pretty much impossible.
If you need more assistance with any of the concepts, check out our in-depth guides to linear equations, systems of equations, absolute value, intercept-slope form, and linear inequalities and systems of inequalities.
Strategy #2: Plugging in Answers
On the multiple-choice questions, you should always check to see if you can plug in the answer choices to the given equation(s) or inequality to find the correct answer. Sometimes this approach will be much simpler than trying to solve the equation.
Even if you find that plugging in answers is slowing you down, you should, at least, consider using it to check your work. Plug in the answer choice that you find and see if it results in a balanced equation or correct inequalities. If it does, you know you have the correct answer!
 Plug it in! Plug it in!
Plug it in! Plug it in!
Strategy #3: Plugging in Numbers
If plugging in answers isn't a possibility, plugging in numbers is often a possibility such as in question 2 above. When you pick numbers to plug in, in general, I do not recommend using -1, 0, or 1 (as they can result in wrong answers), and make sure to read the question to see what numbers you should pick. For example, in question 2, the numbers represented the number of text messages sent, so you shouldn't use a negative number to represent the number of text messages since it's impossible to send a negative number of text messages.
For inequalities this is especially important, often the question will say "the following is true for all $x>0$." If that's the case, you can't plug in 0 or -5; you can only plug in numbers greater than 0 since that's the parameter set by the question.
Strategy #4: Work One Step At a Time
For Heart of Algebra questions, you need to take your time working through each step. These questions can involve 5, 10, 15 steps, and you need to take your time to make sure you don't make a small mistake in step 3 that will result in an incorrect answer. You know your stuff, so don't let small mistakes cost you points!
What's Next?
Now that you know what to expect on Heart of Algebra questions, make sure you're prepared for all of the other math topics you'll see on the SAT. All of our math guides will take you through strategies and practice problems for all the topics covered in the math section, from integers to ratios, circles to polygons (and more!).
Feeling anxious about test day? Make sure you know exactly what to do and bring to ease your mind and settle your nerves before it's time to take your SAT.
Running out of time on the SAT math section? Look no further than our guide to help you beat the clock and maximize your SAT math score.
Angling to get a perfect score? Check out our guide to getting a perfect 800, written by a perfect-scorer.












