
Starting in March 2016, there will be a newly redesigned SAT. The new SAT only has two sections: Evidence-Based Reading and Writing and Math.
While most people are focused on the changes to the Reading and Writing section, there have been a few changes to the SAT Math section that are important to know. What are these changes? How will your SAT study strategy need to change? I'll delve into that and more in this guide.
Math: The Major Changes in the 2016 New SAT
Let's go through each of the important alterations to the math section of the test.
Two Sections: One With Calculator, One With No Calculator
On the old SAT, the whole math section allowed you to use a calculator. On the new SAT, the math section is divided into two portions: one which allows calculator and one which does not. The non-calculator portion will always be the third section of the test. The calculator portion will always be the fourth section of the test.
Don't be afraid of the no-calculator section. The reason you're not allowed a calculator is you should be able to solve these questions without one. Some of the skills required to answer these no calculator questions include:
- Simple math (addition, subtraction, multiplication, division)
- Simplifying single equations or phrases (using the FOIL method)
- Solving a system of two equations
- Knowing square roots (or being able to find a square root by multiplying)
- Being familiar with powers (and how to reconfigure powers).
These questions can get somewhat challenging. Here is a sample no calculator question (from an official practice SAT) that requires you to use your knowledge of powers:
If $3x-y=12$, what is the value of ${8^x}/{2^y}$?
A) $2^12$
B) $4^4$
C) $8^2$
D) The value cannot be determined from the information given.
Answer Explanation:
One approach is to express
$${8^x}/{2^y}$$
so that the numerator and denominator are expressed with the same base. Since 2 and 8 are both powers of 2, substituting $2^3$ for 8 in the numerator of ${8^x}/{2^y}$ gives
$${(2^3)^x}/{2^y}$$
which can be rewritten
$${2^(3x)}/{2^y}$$
Since the numerator and denominator of have a common base, this expression can be rewritten as $2^(3x−y)$. In the question, it states that $3x − y = 12$, so one can substitute 12 for the exponent, $3x − y$, giving that the
$${8^x}/{2^y}= 2^12$$
The final answer is A.
Here is a sample no calculator question that requires you to simplify:
If $x>3$, which of the following is equivalent to $1/{1/{x+2}+1/{x+3}}$?
A) ${2x+5}/{x^2+5x+6}$
B) ${x^2+5x+6}/{2x+5}$
C) $2x+5$
D) $x^2+5x+6$
Answer Explanation:
In order to find the answer, you need to rewrite the original phrase and to do that you need to multiply it by ${(x+2)(x+3)}/{(x+2)(x+3)}$.
When you multiply through, you should get ${(x+2)(x+3)}/{(x+2)+(x+3)}$. Continue simplifying by multiplying $(x+2)(x+3)$ in the numerator and simplifying the denominator by completing the addition of $(x+2)+(x+3)$. You should then get:
$${x^2+5x+6}/{2x+5}$$
That matches answer choice B, so that is the final answer!
Less Emphasis on Geometry
Geometry took up about 25-35% of questions on the old SAT, but it will now account for less than 10% of questions on the new SAT. The questions will remain relatively the same, but there will simply be less of them. Here is a sample Geometry question from a new SAT practice test:

Answer Explanation:
The volume of the grain silo can be found by adding the volumes of all the solids of which it is composed (a cylinder and two cones). The silo is made up of a cylinder (with height 10 feet and base radius 5 feet) and two cones (each with height 5 ft and base radius 5 ft). The formulas given at the beginning of the SAT Math section (Volume of a Cone $V={1}/{3}πr^2h$ and Volume of a Cylinder $V=πr^2h$) can be used to determine the total volume of the silo. Since the two cones have identical dimensions, the total volume, in cubic feet, of the silo is given by
$$V_(silo)=π(5)^2(10)+(2)({1}/{3})π(5)^2(5)=({4}/{3})(250)π$$
which is approximately equal to 1,047.2 cubic feet. The final answer is D.
Also, somewhat ironically, although the number of Geometry questions is decreasing, the College Board decided to give you more Geometry formulas in the reference section, which is at the beginning of the SAT Math sections. The reference section lists some formulas and laws for you to use when answering questions.
Here is the old reference section:
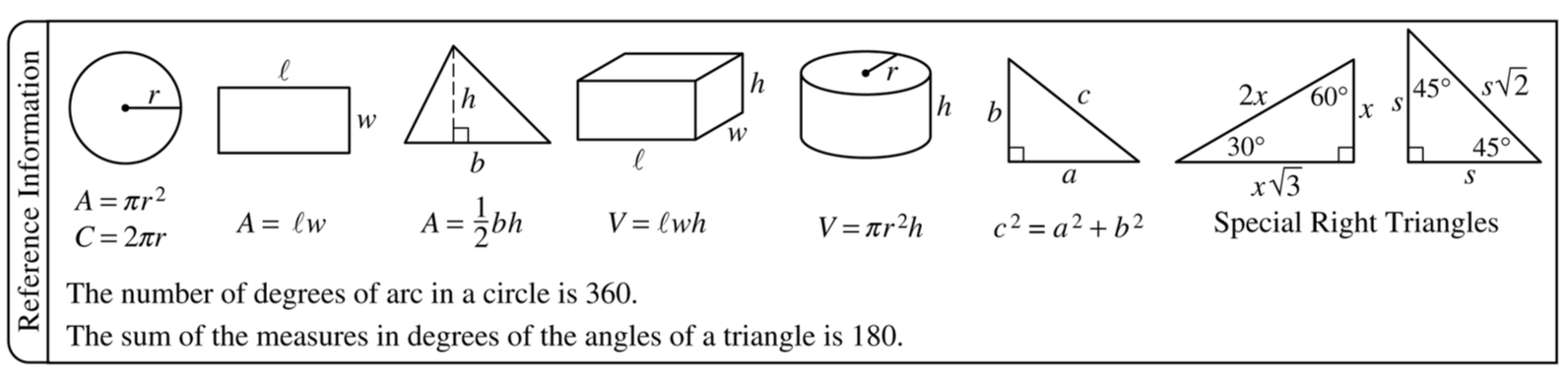
Here is the new reference section:

In addition to the formulas included in the old reference section, the College Board has included the volume formulas for a sphere, cone, and pyramid. Also, the College Board gives you an additional law of Geometry: "the number of radians of arc in a circle is 2π."
For a full list of provided formulas and formulas you should memorize, read our guide to formulas you must know.
Increased Focus on Algebra
Algebra will now account for more than half of the questions in the SAT math section. While algebra was always a part of the math section, it's now being emphasized even more. These questions can be very tricky because they ask you to apply algebra in unique ways. Some of the algebra skills required to succeed on the SAT math section include:
- Solving linear equations
- Solving a system of equations
- Creating linear equations or system of equations to solve problems (used in the example below).
- Creating, analyzing, solving and graphing exponential, quadratic, and other non-linear equations.
The following example algebra question is from a real new SAT practice question:

Answer Explanation:
To solve this problem, you should create two equations using two variables ($x$ and $y$) and the information you're given. Let $x$ be the number of left-handed female students and let $y$ be the number of left-handed male students. Using the information given in the problem, the number of right-handed female students will be $5x$, and the number of right-handed male students will be $9y$. Since the total number of left-handed students is 18 and
the total number of right-handed students is 122, the system of equations below must be true:
$$x + y = 18$$
$$5x + 9y = 122$$
When you solve this system of equations, you get $x = 10$ and $y = 8$. Thus, 50 of the 122 right-handed students are female. Therefore, the probability that a right-handed student selected at random is female is ${50}/{122}$, which to the nearest thousandth is 0.410.
The final answer is A.
Increased Focus on Modeling
The new SAT math section has a new type of question which asks you to think about what equations or models mean. You will be given a model or equation and be asked to explain what certain parts mean or represent. These questions are weird because they're asking you to do something you rarely do: they ask you to analyze the significance of the number or variable in context rather than solve the equation.
Here is a sample modeling question from a new SAT practice test:
Kathy is a repair technician for a phone company. Each week, she receives a batch of phones that need repairs. The number of phones that she has left to fix at the end of each day can be estimated with the equation $P=108-23d$, where $P$ is the number of phones left and $d$ is the number of days she has worked that week. What is the meaning of the value 108 in this equation?
A) Kathy will complete the repairs within 108 days.
B) Kathy starts each week with 108 phones to fix.
C) Kathy repairs phones at a rate of 108 per hour.
D) Kathy repairs phones at a rate of 108 per day.
Answer Explanation: In the given equation, $108$ is the value of $P$ in $P = 108 − 23d$ when $d = 0$. When $d = 0$, Kathy has worked $0$ days that week. In other words, $108$ is the number of phones left before Kathy has started work for the week. Therefore, the meaning of $108$ in the given equation is that Kathy starts each week with $108$ phones to fix because she has worked $0$ days and has $108$ phones left to fix.
The final answer is B.
More Advanced Topics
Addition of Trigonometry
Trigonometry had never been asked on the SAT Math section… until now! Trigonometry will now account for as many as 5% of math questions. You'll be tested on your knowledge of sine and cosine. Here is a sample trigonometry question from a real new SAT practice test:
In triangle $ABC$, the measure of angle $∠ B$ is 90°, $BC=16$, and $AC=20$. Triangle $DEF$ is similar to triangle $ABC$, where vertices $D$, $E$, and $F$ correspond to vertices $A$, $B$, and $C$, respectively, and each side of triangle $DEF$ is $1/3$ the length of the corresponding side of triangle $ABC$. What is the value of sin$F$?
(This is a grid-in question, not multiple choice, so there are no answer choices listed with the question.)
Answer Explanation: Triangle ABC is a right triangle with its right angle at B. Therefore, $\ov {AC}$ is the hypotenuse of right triangle ABC, and $\ov {AB}$ and $\ov {BC}$ are the legs of right triangle ABC. According to the Pythagorean theorem,
$$AB =√{20^2-16^2}=√{400-256}=√{144}=12$$
Since triangle DEF is similar to triangle ABC, with vertex F corresponding to vertex C, the measure of $\angle ∠ {F}$ equals the measure of $\angle ∠ {C}$. Therefore, $sin F = sin C$. From the side lengths of triangle ABC,
$$sinF ={\opposite \side}/{\hypotenuse}={AB}/{AC}={12}/{20}={3}/{5}$$
Therefore, $sinF ={3}/{5}$.
The final answer is ${3}/{5}$ or 0.6.
Addition of i
Questions asking you to use $i$ have been added to the new SAT math section. On the exam, problems that use $i$ will always remind you that $i=√(-1)$. However, you should know that this also means $i^2=-1$. You should otherwise approach problems that use $i$ in the same way you'd approach any other math problem. Let's attempt this $i$ example problem below:
$${8-i}/{3-2i}$$
If the expression above is written in the form $a+bi$, where $a$ and $b$ are real numbers, what is the value of $a$? (Note: $i=√{-1}$)
A) $2$
B) $8/3$
C) $3$
D) $11/3$
Answer Explanation: To rewrite ${8-i}/{3-2i}$ in the standard form $a + bi$, you need to multiply the numerator and denominator of ${8-i}/{3-2i}$ by the conjugate, $3 + 2i$. This equals
$$({8-i}/{3-2i})({3+2i}/{3+2i})={24+16i-3i+(-i)(2i)}/{(3^2)+(2i)^2}$$
Since $i^2=-1$, this last fraction can be reduced simplified to
$$ {24+16i-3i+2}/{9-(-4)}={26+13i}/{13}$$
which simplifies further to $2 + i$. Therefore, when${8-i}/{3-2i}$ is rewritten in the standard form $a + bi$, the value of a is 2.
The final answer is A.
How Does Your Study Strategy for SAT Math Need to Change?
Let's go through the key steps you need to take to prepare for this new version of the test.
Practice Mental Math
Since there is a non-calculator portion of the new SAT math section, you need to be prepared to do math without a calculator! Make sure you're sharp on your basic math skills (adding (including adding fractions), subtracting, multiplying, dividing). Also, make sure you know some common square roots (and squared numbers).
My advice for making sure you're ready for the non-calculator portion of the new SAT math section is to practice a lot. Make sure you take every free new SAT practice test available. Don't use your calculator on the non-calculator section and see how you do!
Practice makes perfect! However, to get really good at your mental math, you need to stick to the real testing conditions. Realistic practice makes perfect!

Spend Most of Your Study Time on Algebra
Since algebra counts for 50% or more of the new SAT math section, you need to make sure your algebra skills are at maximum strength! Check out our two fantastic algebra guides for help with systems of equations and linear, quadratic, and algebraic functions. Make sure you get realistic practice. Take every free new SAT practice test available, and make sure to do a thorough review of your test.
Get Familiar With Advanced Topics
For trigonometry, don't worry about spending too much time on it since it accounts for less than 5% of questions, but you should make sure you know the basic trigonometry formulas you'll need to use and how to apply them.
If you have the basic trigonometry formulas (sine and cosine) memorized and know how to apply them, then you should be able to answer most SAT math trigonometry questions. Since trigonometry only accounts for about 5% of the math section, only spend about 5% of your SAT math study time on it.
For $\bi i$, also don't worry too much. There are usually only 1-3 $i$ questions per test. As I said before, the problems that use $i$ will always remind you that $i=√(-1)$. Just make sure you remember that if $i=√(-1)$ then $i^2=-1$. If you keep this in mind, you should be able to solve the $i$ questions on the SAT.
The Bottom Line
Though the changes to the new SAT math section might feel major, they're actually relatively subtle. There has been a slight shift in the material covered, which means there needs to be a shift in how much time you spend studying certain math topics. The questions asked are generally more straightforward than those on the previous SAT math.
The Major Changes to Math Are:
#1: Less geometry (down to less than 10%)
#2: More algebra and modeling (50% or more of the test)
#3: Trigonometry and $i$ have been added
#4: You're not allowed to use your calculator on one portion of the math test
You Should Change Your Study Strategy By:
#1: Knowing your mental math
#2: Focusing your time on algebra
#3: Learning trigonometry and $i$ (but not spending too much time on them)
What's Next?
Need to brush up on some basic math in preparation for the no-calculator section? Our articles on the distributive property, perfect squares, inequalities, adding and subtracting fractions, and tips for easy multiplication can help.
Want a ratio and proportions challenge? Try calculating how many seconds there are in a day, week, and year, then check your process and answers here!
Interested in testing yourself with the hardest SAT math questions out there? Check out our 13 toughest SAT math question guide.
Running out of time on the SAT math section? Our guide will help you beat the clock and maximize your score.
Aiming for a perfect score? Check out our guide on how to get a perfect 800 on the SAT math section, written by a perfect scorer.












